四邊形面積

---

簡介

四邊形的面積是指四邊形各邊所包圍的區域。四邊形包含的領土數量決定了它的面積。讓我們回顧一下四邊形的定義。一個封閉的圖形，由四條線段圍成，稱為四邊形。四邊形既有正規的，也有不規則的。等邊四邊形是指邊長相等的四邊形。不規則四邊形是不規則的四邊形。

四邊形有六種不同的型別。正方形、矩形、平行四邊形、梯形、菱形、風箏等。在本教程中，我們討論了所有這些四邊形的面積。我們將研究如何將四邊形分成兩個三角形，以及如何透過計算其四條邊來計算其面積。我們還將學習計算每種不同四邊形形狀面積的公式。

四邊形

在幾何學中，四邊形是一個封閉的圖形，它是由連線四個點形成的，其中任意三個點不共線。一個四邊形有4條邊、4個角和4個頂點。四邊形的所有四條邊不一定相等。命名四邊形時，必須考慮頂點的排列順序。

例如，以下四邊形應稱為PQRS、QRSP、PSRQ或RSPQ。由於它們改變了生成四邊形的頂點順序，因此不能稱為PRSQ或SQPR。一個標有PQRS的四邊形有四條邊：PQ、QR、RS和PS，以及兩條對角線：PR和QS。

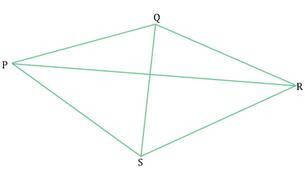
不同四邊形的面積

四邊形包含的領土數量決定了它的面積。四邊形包括正方形、矩形、平行四邊形、梯形、菱形、風箏等。

除了學習如何將四邊形分成兩個三角形外，您還將學習如何計算四邊形的邊數以確定其面積。此外，我們還將學習計算每種不同

正方形和矩形

正方形是一種四邊形，其四條邊長度相等，四個角的度數也相等，均為90度。如果正方形每條邊的長度為a，則計算正方形面積的公式為邊²

$$\mathrm{面積 =a^2, 其中\: a\: 是\: 邊的\: 長度}$$

示例

邊長為3釐米的正方形的面積為3²=9平方釐米

在矩形四邊形中，一對對邊相等且平行，每個角的度數為90度。如果矩形的長和寬分別為l和b，則計算矩形面積的公式為長×寬=lb

示例

長為2釐米、寬為1釐米的矩形的面積為lb=2(1)=2平方釐米

菱形和平行四邊形

在菱形中，所有邊長度相等，且成對的對邊平行。對角相等，對角線相互垂直平分。如果d₁和d₂是兩條對角線的長度，則菱形的面積由公式$\mathrm{\frac{1}{2}×d_1×d_2}$給出

示例

對角線長度分別為5釐米和8釐米的菱形的面積為$\mathrm{\frac{1}{2}×d_1×d_2=\frac{1}{2}×5×8=20}$平方釐米

在平行四邊形中，成對的對邊相等且平行。成對的對角相等，對角線互相平分。如果b是底邊，h是平行四邊形的高，則其面積由底×高=bh計算得出。

示例

底邊為10釐米、高為4釐米的平行四邊形的面積為bh=10(4)=40平方釐米

梯形

在梯形中，只有一對對邊平行。如果a和b是兩條平行對邊的長度，h是它們之間的距離，即四邊形的高，則梯形的面積由公式$\mathrm{\frac{1}{2}×(a+b)×h}$給出

示例

如果梯形中兩條平行邊的長度分別為5釐米和7釐米，它們之間的距離為4釐米，則其面積為$\mathrm{\frac{1}{2}×(a+b)×h=\frac{1}{2}×(5+7)×4=12×2=24 }$平方釐米

風箏

以下是幾何圖形風箏UVWZ，其中UV=UZ，VW=ZW

即鄰邊長度相等，對角線在點O處互相平分。

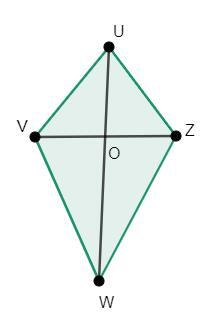
風箏的面積可以透過將兩個三角形區域（即UVZ和VWZ）的面積相加來求得。也可以使用對角線的長度來求出風箏的面積。

如果d₁和d₂是兩條對角線的長度，則風箏的面積由公式$\mathrm{\frac{1}{2}×d_1×d_2}$給出

一般四邊形

以下四邊形是一個一般四邊形。它的面積可以透過將由於任何一條對角線而被分成兩個三角形的面積相加來求得。

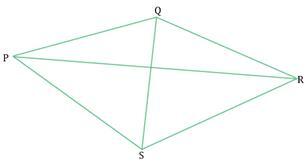
示例

$$\mathrm{ar(PQRS)=ar(PQS)+ar(QRS) 或 =ar(PQR)+ar(PSR)}$$

例題解析

1）計算對角線分別為16和14的風箏的面積。

答案：已知d₁=16和d₂=14

因此，給定風箏的面積確定為

$$\mathrm{\frac{1}{2}×d_1×d_2=\frac{1}{2}×16×14=112 \:平方單位}$$

2）使用四邊形面積公式，求底邊分別為12英寸和8英寸，高為4英寸的梯形的面積。

答案：已知a=12英寸，b=8英寸和h=4英寸

使用公式，

梯形的面積由下式給出

$$\mathrm{\frac{1}{2}×(a+b)×h=\frac{1}{2}×(12+8)×4=20×2=40\: 平方英寸}$$

3）使用海倫公式確定以下四邊形的面積

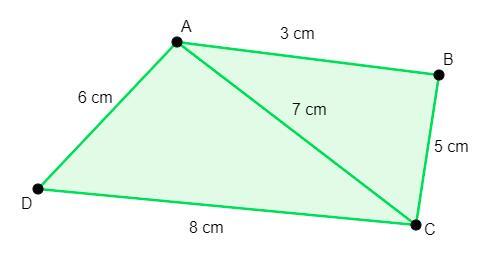
答案：使用海倫公式求三角形ABC的面積 -

$$\mathrm{s=\frac{3+5+7}{2}=7.5}$$

所以，

$$\mathrm{面積=\sqrt{s(s-a)(s-b)(s-c)}=\sqrt{7.5(7.5-3)(7.5-5)(7.5-7)}=\sqrt{42.1875}}$$

使用海倫公式求三角形ADC的面積 -

$$\mathrm{s=\frac{6+7+8}{2}=10.5}$$

所以，

$$\mathrm{面積=\sqrt{10.5(10.5-6)(10.5-7)(10.5-8)}=\sqrt{413.4375}}$$

因此，所需四邊形的面積由下式給出

$$\mathrm{面積=\sqrt{42.1875}+\sqrt{413.4375}\: 平方單位}$$

結論

• 四邊形的表面積是四邊形邊界之間區域的面積。

• 如上所述，有不同型別的四邊形，以及各自的面積計算公式。

常見問題

1. 如何計算四邊形的面積？

如果已知對角線和從頂點到對角線的垂線的長度，則四邊形的面積計算如下 -

四邊形的面積 = (1/2) 對角線長度 x 從其餘兩個頂點引出的垂線的長度之和。

2. 哪種四邊形的邊長相等？

一個封閉的圖形，由四條線段圍成，稱為四邊形。四邊形既有正規的，也有不規則的。等邊四邊形是指邊長相等的四邊形。

3. 四邊形的名稱是什麼？

四邊形是一種有四條邊和四個角的圖形。任何邊長相等的四邊形都被稱為正四邊形。不規則四邊形是指邊長不相等的四邊形，因為它不是正四邊形。

4. 關於四邊形，有三個事實是什麼？

四邊形是一種有四條邊和四個角的多邊形。四邊形一詞源於quad（意為四）和lateral（意為邊）。四邊形的內角之和為360度。

5. 四邊形之間有什麼聯絡？

四邊形有很多不同的種類，但它們都有四條邊、兩條對角線，並且內角之和為360度。它們彼此之間都有聯絡，但它們都是獨一無二的，並且具有不同的特性。