在問題 4 中，點\( \mathrm{C} \) 被稱為線段\( \mathrm{AB} \) 的中點。證明每條線段都只有一箇中點。

已知

點 $C$ 是 $\overline{AB}$ 的中點。

要做的

我們必須證明每條線段都只有一箇中點。

解決方案

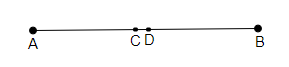
假設點 $C$ 和 $D$ 是 $\overline{AB}$ 的兩個中點。

由於，$C$ 和 $D$ 是 $\overline{AB}$ 的中點。

我們得到，

$AC=CB$ 和 $AD=BD$

根據歐幾里得公理

我們得到，

$AC+CB=AB$  (因為，$AC+CB$ 與 $AB$ 重合)

類似地，我們得到，

$AD+BD=AB$  (因為，$AD+BD$ 與 $AB$ 重合)

現在， 

在 $AC=CB$ 的兩邊加上 $AC$

我們得到，

$AC+AC=CB+AC$ (因為，如果相等的東西加到相等的東西上，那麼整體也是相等的。)

這意味著，

$2AC=AB$...........(i)

以類似的方式，我們得到，

$AD+AD=DB+AD$  (因為，如果相等的東西加到相等的東西上，那麼整體也是相等的。)

這意味著，

$2AD=AB$.............(ii)

從 (i) 和 (ii)

我們得到 RHS 相同 

因此，

讓我們將 (i) 和 (ii) 的 LHS 等價

我們得到，

$2AC=2AD$ (根據歐幾里得公理：等於同一事物的事物彼此相等。)

因此，

$AC=AD$(根據歐幾里得公理：等於同一事物兩倍的事物彼此相等。)

因此，

我們可以說點 $C$ 和 $D$ 是相同的點。

因此， 

我們假設 $C$ 和 $D$ 是兩個不同的中點的假設是錯誤的。

因此，每條線段都只有一箇中點。

證畢。

教程點

更新於： 2022 年 10 月 10 日

74 次檢視

開啟你的 職業生涯

透過完成課程獲得認證

開始學習