下圖中，$\angle B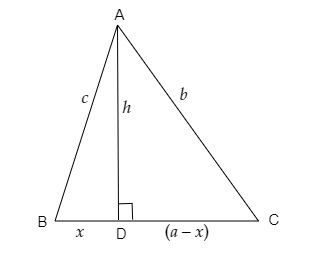"\n

已知

$\angle B<90^o$ 且線段 $AD \perp BC$。

求證

我們需要證明 $b^2=a^2+c^2-2ax$。

證明

在 $\triangle ADC$ 中，根據勾股定理，

$ AC^2=AD^2+DC^2$

$b^2=h^2+(a-x)^2$

$b^2=h^2+a^2+x^2-2ax$.....(i)

在 $\triangle ADB$ 中，根據勾股定理，

$ AB^2=AD^2+DB^2$

$c^2=h^2+x^2$.......(ii)

將式 (ii) 代入 (i)，我們得到，

$b^2=(h^2+x^2)+a^2-2ax$

$b^2=c^2+a^2-2ax$

$b^2=a^2+c^2-2ax$

於是，證明完畢。

Tutorialspoint

更新於： 2022-10-10

35 次瀏覽

開啟你的 職業生涯

完成課程拿到認證

立即開始