資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會研究
服裝研究
法律研究在直角三角形ABC中，∠B=90°，以AB為直徑作圓，該圓與斜邊AC相交於點P。證明該圓在P點的切線平分BC。
已知
在直角三角形ABC中，∠B=90°，以AB為直徑作圓，該圓與斜邊AC相交於點P。
要求
證明該圓在P點的切線平分BC。
解答
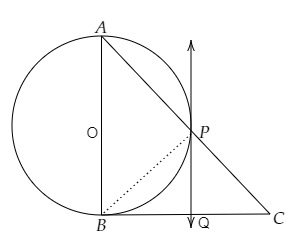
設O為已知圓的圓心。
設在P點的切線與BC相交於Q點。
連線BP。
∠ABC = 90° (圓上任意一點的切線垂直於經過該點的半徑)
在△ABC中，
∠CAB + ∠BCA = 90° (角和性質和∠ABC = 90°)
∠BPQ = ∠BAC (切線與弦的夾角等於弦在另一弓形中所對的角)
∠BPQ + ∠BCA = 90° ……..(i)
∠APB = 90° (半圓中的圓周角)
∠BPQ + ∠CPQ = 90° …….(ii) (∠APB + ∠BPC = 180°，鄰補角)
由公式(i)和(ii)，我們得到：
∠BPQ + ∠BCP = ∠BPQ + ∠CPQ
∠BCP = ∠CPQ
PQ = QC (等角對等邊)
QP = QB (從圓內一點引出的兩條切線相等)
QB = QC
證畢。
更新於：2022年10月10日
53 次瀏覽
廣告