畫一對正切於半徑為 3 釐米的圓的切線，它們彼此的傾角為 $60^{o}$。

已知：圓的半徑為 3 釐米。

需要做：畫一對正切於圓的切線，它們彼此的傾角為 $60^{o}$。

解答： 

按照以下步驟繪製所需的圖形。

1. 以 O 為圓心畫一個半徑為 3 釐米的圓。

2. 這裡切線彼此的傾角為 $60^{o}$。如果 PA 和 PB 是圓的所需切線，則 $\angle APB=60^{o}$，並且 AOBP 是一個圓內接四邊形，則 $\angle AOB=180^{o} -60^{o} =120^{o}。$

3. 在給定圓的圓周上取一點 A，並在點 O 處畫一個與 OA 成 120° 角的角，使得 $\angle AOB=120^{o}$。B 是另一個點，其中 $\angle AOB=120^{o}$ 與圓相交。

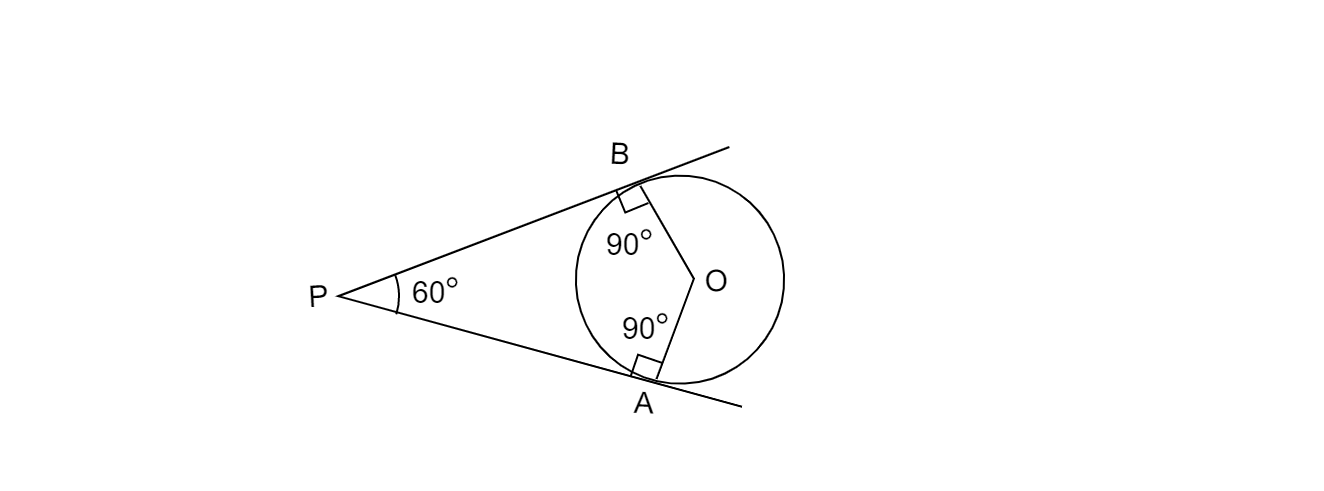
4. 畫一條垂直於 OA 的線。

5. 畫一條垂直於 OB 的線。

6. A 和 B 上的垂線在點 P 相交。

因此，PA 和 PB 是圓的所需的一對切線，它們彼此的傾角為 $60^{o}$。