將多項式 $p(x)$ 除以多項式 $g(x)$，求商和餘數
$p(x) = x^4 - 5x + 6, g(x) = 2 -x^2$

學術數學 NCERT 10年級

已知

$p(x) = x^4 - 5x + 6, g(x) = 2 -x^2$

要求

我們需要將多項式 $p(x)$ 除以多項式 $g(x)$，並求出商和餘數。

解答

$p(x) = x^4 - 5x + 6$

$g(x) = 2 -x^2$

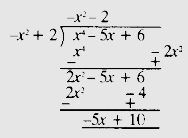
因此，商為 $-x^2-2$，餘數為 $-5x+10$。

教程點 (Tutorialspoint)

更新於：2022年10月10日

瀏覽量：79

相關文章
將多項式 $p(x)$ 除以多項式 $g(x)$，求商和餘數，如下所示：(i) $p(x) = x^3 - 3x^2 + 5x -3, g(x) = x^2-2$(ii) $p(x) =x^4 - 3x^2 + 4x + 5, g(x) = x^2 + 1 -x$(iii) $p(x) = x^4 - 5x + 6, g(x) = 2 -x^2$
將多項式 $p(x)$ 除以多項式 $g(x)$，求商和餘數，如下所示：$p(x) =x^4 - 3x^2 + 4x + 5, g(x) = x^2 + 1 -x$
將多項式 $p(x)$ 除以多項式 $g(x)$，求商和餘數，如下所示：$(p(x)=x^3 - 3x^2 + 5x - 3, g(x) = x^2 - 2)$。
將 $x^3 - 3x^2 + x + 2$ 除以多項式 $g(x)$，商為 $x - 2$，餘數為 $-2x + 4$。求 $g(x)$。
利用因式定理判斷在下列每種情況下 \( g(x) \) 是否為 \( p(x) \) 的因式：(i) \( p(x)=2 x^3 + x^2 - 2x - 1, g(x) = x + 1 \)(ii) \( p(x) = x^3 + 3x^2 + 3x + 1, g(x) = x + 2 \)(iii) \( p(x) = x^3 - 4x^2 + x + 6, g(x) = x - 3 \)
回答並說明理由：如果將多項式 \( p(x) \) 除以多項式 \( g(x) \) 的商為零，那麼 \( p(x) \) 和 \( g(x) \) 的次數之間有什麼關係？
求多項式 $P(x) = x^2 - 5x + 6$ 的零點。
回答並說明理由：如果將非零多項式 \( p(x) \) 除以多項式 \( g(x) \) 的餘數為零，那麼 \( p(x) \) 和 \( g(x) \) 的次數之間有什麼關係？
用除法演算法求將 $f(x)$ 除以 $g(x)$ 時的商 $q(x)$ 和餘數 $r(x)$：$f(x) = x^3 - 6x^2 + 11x - 6, g(x) = x^2 + x + 1$
求多項式 \( x^2 + x - p(p+1) \) 的零點。
在下列每種情況下，用因式定理判斷多項式 $g(x)$ 是否為多項式 $f(x)$ 的因式：$f(x) = x^3 - 6x^2 + 11x - 6, g(x) = x^2 - 3x + 2$
在下列每種情況下，用因式定理判斷多項式 $g(x)$ 是否為多項式 $f(x)$ 的因式：$f(x) = x^5 + 3x^4 - x^3 - 3x^2 + 5x + 15, g(x) = x + 3$
用除法演算法求將 $f(x)$ 除以 $g(x)$ 時的商 $q(x)$ 和餘數 $r(x)$：$f(x) = 15x^3 - 20x^2 + 13x - 12, g(x) = x^2 - 2x + 2$
在下列每種情況下，用因式定理判斷多項式 $g(x)$ 是否為多項式 $f(x)$ 的因式：$f(x) = x^3 - 6x^2 + 11x - 6; g(x) = x - 3$
利用餘數定理，求 $f(x)$ 除以 $g(x)$ 的餘數：$f(x) = 4x^3 - 12x^2 + 11x - 3, g(x) = x + \frac{1}{2}$。

開啟你的職業生涯

完成課程獲得認證

廣告

© . All rights reserved.