已知等邊三角形的邊長，作圖構造該等邊三角形並說明作圖依據。

待辦事項

我們需要構造一個等邊三角形，已知其邊長，並說明構造的依據。

解答

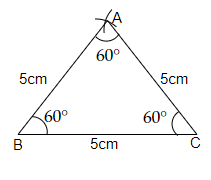
作圖步驟

(i) 作一條線段 $BC$，長度為 $5\ cm$。

(ii) 以點 $B$ 為圓心，半徑為 $5\ cm$ 作弧；以點 $C$ 為圓心，半徑為 $5\ cm$ 作弧。

(iii) 將兩弧的交點命名為點 $A$。

(iv) 連線 $AC$ 和 $BC$。$\Delta ABC$ 即為所求三角形。

證明

在 $\Delta ABC$ 中，我們有：

$BC= 5\ cm$，$\angle B=60^o$ 和 $\angle C=60^o$

我們知道：

三角形內角和始終等於 $180^o$

$\angle A+\angle B+\angle C = 180^o$

這意味著：

$\angle A+60^o+60^o=180^o$

$\angle A+ 120^o=180^o$

$\angle A=60^o$

我們知道：

等角對等邊

因此，我們得到：

$CA=AB=5\ cm$

我們有：

$BC=CA=AB=5\ cm$ 並且

$\angle A=\angle B=\angle C=60^o$

因此，得證。

教程點

更新於: 2022年10月10日

56 次瀏覽

開啟你的 職業生涯

完成課程獲得認證

開始學習