在已知射線的起點作一個90°角，並說明作圖的理由。

待辦事項

我們需要在已知射線的起點作一個90°角，並說明作圖的理由。

解答

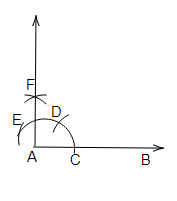
作圖步驟

(a) 畫一條射線AB。

(b) 以A為圓心，適當的半徑畫弧，使它與AB相交於C。

(c) 以C為圓心，相同的半徑在上面畫弧與D相交。

(d) 以D為圓心，相同的半徑在上面畫弧與E相交。

(e) 以D和E為圓心，半徑大於$\frac{1}{2}DE$畫兩條弧，在F點相交。

(f) 連線AF並延長形成射線AF。

因此，

$\angle BAF = 90^o$。

證明

證明$\angle BAF=90^o$

讓我們從A到D和O到E畫一條虛線。

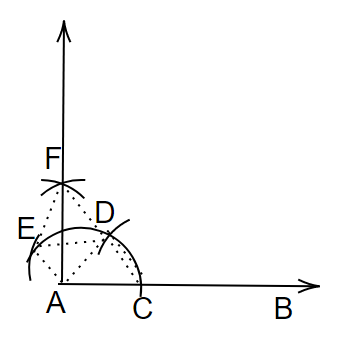
我們有，

$AC=CD=AD$

因此，

$ACD$是一個等邊三角形

這意味著，

$\angle CAD=60^o$

同樣地，我們得到，

$AE=DE=AD$

因此，

$ADE$是一個等邊三角形

這意味著，

$\angle EAD=60^o$

根據SSS全等定理，我們得到，

$\triangle ACD \cong \triangle ADE$

根據全等三角形對應角相等，我們得到，

$\angle CAD=\angle EAD$

因此，

$\angle DAF=\frac{1}{2}\angle EAD=\frac{1}{2}(60^o)=30^o$

這意味著，

$\angle DAF=30^o$

$\angle BAF=\angle BAD+\angle DAF$

$=60^o+30^o$

$=90^o$

因此，證明完畢。

教程點

更新於：2022年10月10日

56 次瀏覽

啟動你的職業生涯

完成課程獲得認證

開始學習