資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究作一個三角形\( \mathrm{PQR} \)，其中\( \mathrm{QR}=6 \mathrm{~cm}，\angle \mathrm{Q}=60^{\circ} \)且\( \mathrm{PR}-\mathrm{PQ}=2 \mathrm{~cm} \)。
已知
$QR=6\ cm, \angle Q=60^o$ 且 $PR-PQ=2\ cm$.
要求
我們需要作一個$\triangle PQR$。
解答
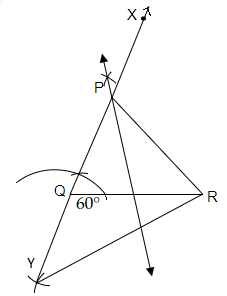
作圖步驟
(i) 我們先畫一條長度為 $6\ cm$ 的線段 $QR$。
(ii) 然後，作一個角 $RQX$，使得 $\angle RQX=60^o$
(iii) 現在，用圓規測量 $PR-PQ=2\ cm$，從點 $Q$ 畫一個弧，並標記為點 $Y$。由於 $PQ-PR$ 為負，所以直線 $QY$ 將線上段 $QR$ 下方。
(v) 現在，用圓規從點 $Q$ 在 $QX$ 上畫另一個弧。
(vi) 現在，連線 $YR$。然後用圓規作線段 $YR$ 的垂直平分線，並將平分線與射線 $QX$ 的交點標記為 $P$
(v) 現在，連線 $PR$。因此，$PQR$ 是所求的三角形。
更新於: 2022年10月10日
57 次瀏覽
廣告