資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
服裝設計
法律一架飛機在地面300米的高度飛行，在這個高度飛行時，飛機上觀察到河兩岸相對方向的兩點的俯角分別為45度和30度。求這條河的寬度。[使用$\sqrt{3} = 1.732$])
已知：飛機高度$=300\ m$，飛機上觀察到河兩岸相對方向的兩點的俯角分別為$45^{o}$ 和 $30^{o}$。
求解：求這條河的寬度。
解答
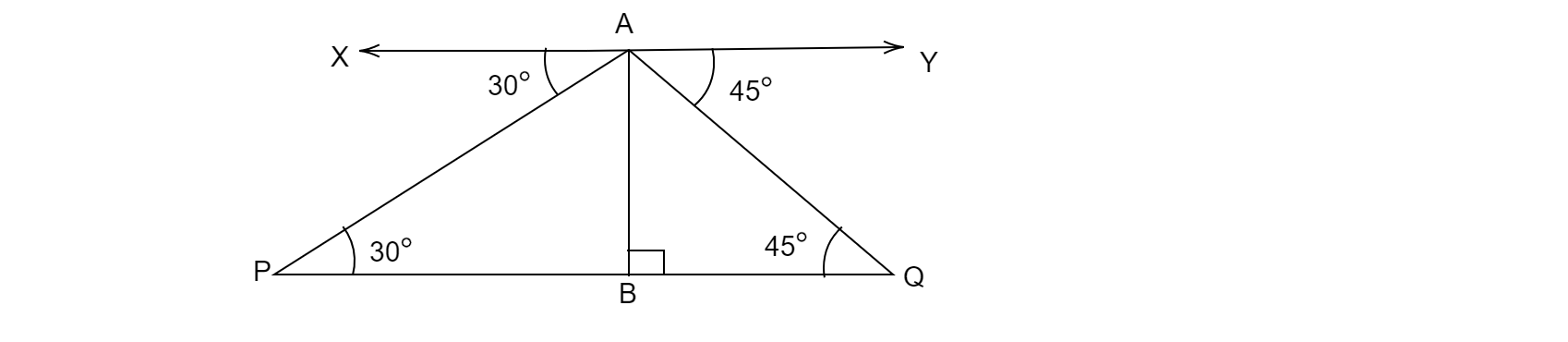
已知飛機的高度為$300\ m$。
$AB=300\ m$ 且 $XY || PQ$。
兩點 $P$ & $Q$ 的俯角分別為 $30^{o}$ 和 $45^{o}$。
$\angle XAP=30^{o}$ & $\angle YAQ=45^{o}$
$\angle XAP\ =\angle APB=30^{o} \&\ \angle YAQ=\angle AQB=45^{o}$
在 $\vartriangle APB$ 中，
$tan 30^{o}=\frac{AB}{PB}$
$\frac{1}{\sqrt{3}} =\frac{AB}{PB}$
$PB=AB\sqrt{3} =300\sqrt{3} \ m$
在 $\vartriangle BAQ$ 中，
$tan45^{o}=\frac{AB}{BQ}$
$1=\frac{300}{BQ}$
$BQ=300\ m$
河寬 $PQ=PB+BQ=300+300\sqrt{3} =300( 1+\sqrt{3}) \ 米$。
更新於: 2022年10月10日
1K+ 瀏覽量
廣告