資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究阿基拉去她村裡的一個集市。她想玩旋轉木馬和套圈遊戲（一種你用圈套住攤位上物品的遊戲，如果圈完全覆蓋了任何物品，你就可以得到它）。她玩套圈遊戲的次數是她乘坐旋轉木馬次數的一半。每次乘坐旋轉木馬要花費3盧比，玩一次套圈遊戲要花費4盧比。如果她在集市上花了20盧比，請用代數和圖形表示這種情況。
已知
阿基拉玩套圈遊戲的次數是她乘坐旋轉木馬次數的一半。
每次乘坐的費用 = 3 盧比
玩一次套圈遊戲的費用 = 4 盧比。
在集市上花費的總金額 = 20 盧比。
要求
我們需要用代數和圖形表示上述情況。
解答
設 $x$ 為阿基拉乘坐旋轉木馬的次數，$y$ 為她玩套圈遊戲的次數。
根據題意，
$y = \frac{1}{2}x$
$\Rightarrow x-2y = 0$.....(i)
$3x + 4y = 20$......(ii)
$4y=20-3x$
$y=\frac{20-3x}{4}$
為了用圖形表示上述方程，我們需要每個方程至少兩個解。
對於方程 (i)，
如果 $x=0$，則 $y=\frac{0}{2}=0$
如果 $x=2$，則 $y=\frac{2}{2}=1$
| $x$ | 0 | 2 |
| $y=\frac{1}{2}x$ | 0 | 1 |
對於方程 (ii)，
如果 $x=0$，則 $y=\frac{20-3(0)}{4}=5$
如果 $y=0$，則 $0=\frac{20-3x}{4}$
$\Rightarrow 20=3x$
$\Rightarrow x=\frac{20}{3}$，這不是整數，因此不容易在座標紙上繪製。
所以，讓我們取 $y=2$
如果 $y=2$，則 $2=\frac{20-3x}{4}$
$\Rightarrow 20-3x=8$
$\Rightarrow 3x=20-8$
$\Rightarrow x=\frac{12}{3}$
$\Rightarrow x=4$
| $x$ | 0 | $\frac{20}{3}$ | 4 |
$y=\frac{20-3x}{4}$ | 5 | 0 | 2 |
上述情況可以用圖形表示如下
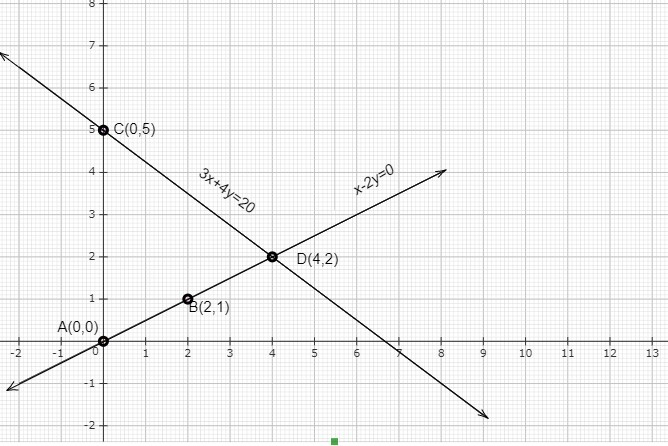
直線 AB 表示方程 $x-2y=0$，直線 CD 表示方程 $3x+4y=20$。
兩條直線在 D(4,2) 點相交，這是兩個方程的解。
278 次瀏覽
