資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究一個人從點\( A \)出發走到點\( \mathrm{D} \)。他從\( \mathrm{A} \)向北走\( 800 \mathrm{~m} \)到達點\( \mathrm{B} \)。從\( \mathrm{B} \)向東走\( 500 \mathrm{~m} \)到達點C。從\( \mathrm{C} \)再次向北走\( 400 \mathrm{~m} \)到達點\( D \)。求點\( \mathrm{A} \)和點\( \mathrm{D} \)之間的直線距離。
已知
一個人從點\( A \)出發走到點\( \mathrm{D} \)。他從\( \mathrm{A} \)向北走\( 800 \mathrm{~m} \)到達點\( \mathrm{B} \)。從\( \mathrm{B} \)向東走\( 500 \mathrm{~m} \)到達點C。從\( \mathrm{C} \)再次向北走\( 400 \mathrm{~m} \)到達點\( D \)。
要求
我們需要求點\( \mathrm{A} \)和點\( \mathrm{D} \)之間的直線距離。
解答
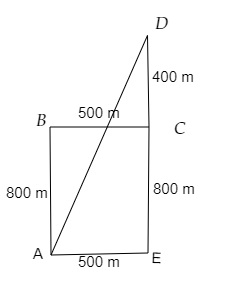
從圖中可以看出，
點\( \mathrm{A} \)和點\( \mathrm{D} \)之間的直線距離 = 三角形AED的斜邊
根據勾股定理，
$AD^2=AE^2+DE^2$
$AD^2=(500)^2+(800+400)^2$
$=250000+1440000$
$=1690000$
$=(1300)^2$
$AD=1300\ m$
點\( \mathrm{A} \)和點\( \mathrm{D} \)之間的直線距離為1300米。
更新時間： 2022年10月10日
57 次瀏覽
廣告