集中趨勢的度量：眾數、中位數、平均數

---

介紹

集中趨勢的度量，也稱為中心度量或中心位置度量，是指試圖用單個值來表示整個資料集的彙總度量，該值顯示分佈的中心值。

三種主要的集中趨勢度量分別是眾數、中位數和平均數。這些值中的每一個都顯示了分佈中心值的不同的指示。

眾數

分佈中最常出現的值是眾數。考慮一下被選中參加某項比賽的 11 名運動員的年齡。

16,16,16,17,17, 18, 18, 19, 20, 21, 21

下表顯示了運動員年齡資料的頻數分佈

年齡	頻數
16	3
17	2
18	2
19	1
20	1
21	2

這裡最常見的值是 16。因此，資料的眾數是 16 歲。

眾數的優點

眾數的主要優點是可以計算數值資料和非數值資料。中位數和平均數則不能。

眾數的侷限性

• 在某些情況下，眾數可能無法清楚地表示資料集的中心。當運動員年齡的分佈按升序排列時，我們得到

  16,16,16,17,17,18,18, 19,20,21,21

  很容易看出這裡的中心值是 18，而不是 16。但是，眾數將中心值表示為 16。

• 資料可能有多個眾數。考慮以下關於運動員年齡的資料集。

  16,16,16,17,17,18,18,18,19,20,21

  在這裡，我們可能得到兩個眾數——16 和 18。因此，它是**雙峰的**。值得注意的是，在大多數情況下也存在**多峰**資料集。因此，在許多情況下，不可能透過眾數找到一個集中趨勢的度量，因為可能存在多個最常見的資料值。

• 現在，考慮一個連續的資料集。

  16,17,18,19,20,21,22,23,24,25,26

  在這裡，運動員年齡的資料是連續的，根本沒有眾數。因此，對於連續資料集，可能沒有眾數。

中位數

中位數是資料集在按升序或降序排列時的中間值。

對於運動員的年齡，我們得到按升序排列的資料集

16,16,16,17,17,18,18, 19,20,21,21

這裡的中間值是 18。因此，中位數是 18。

當資料集具有偶數個觀測值時，兩個中間值的平均值作為中位數。考慮以下資料集。

16,16,16,17,17,18,19, 19,20,21,21, 21

此資料集的中位數將是 18 和 19 的平均值，即 18.5。因此，在這種情況下，中位數是 18.5。

中位數的優點

• 中位數通常比平均數受偏斜資料的影響較小。它也較少受異常值的影響。這就是為什麼它被認為是用於非對稱資料分佈集的理想選擇。

中位數的侷限性

• 中位數的一個缺點是它無法用於分類名義資料，因為很難進行邏輯排序。

平均數

平均數是資料的算術平均值。換句話說，平均數是透過將所有資料加起來，然後將結果除以資料個數獲得的。

再次檢視運動員的年齡，我們有

16,16,16,17,17, 18, 18, 19, 20, 21, 21

運動員年齡的總和是 16+16+16+17+17+18+18+19+20+21+21=199

現在，將總和除以 11，我們得到 18.09

因此，18.09 是資料集的平均數。

平均數的優點

• 它可用於連續和離散資料集。

平均數的侷限性

• 平均數無法用於分類資料，因為資料無法求和。

• 平均數受異常值和偏斜資料的影響，因為它包含所有資料值。

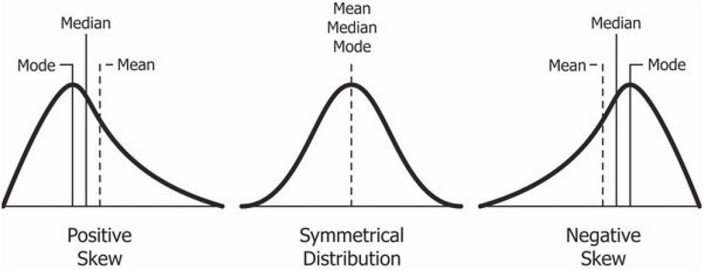
分佈的形狀如何影響集中趨勢

對稱分佈

當資料集是對稱時，眾數、中位數和平均數都落在分佈的中間。例如，對於更大的運動員年齡資料集，當資料是對稱時，平均數、中位數和眾數都可能落在 18 歲。

偏斜分佈

在偏斜分佈的情況下，眾數和中位數保持不變，但平均數被拉向尾部。在偏斜分佈的情況下，中位數通常是首選的集中趨勢，因為平均數不在分佈的中心位置。

正偏或右偏分佈的右側尾部比分佈的左側尾部大。在右偏分佈的情況下，平均數通常被拉向分佈的右側。在負偏或左偏分佈的情況下，平均數被拉向分佈的左側。

異常值如何影響集中趨勢的度量

異常值是與資料集中可以找到的一般資料值大相徑庭的極端資料值。異常值會改變資料分析的結果，因此在考慮集中趨勢的度量時必須檢測到它們。

考慮運動員年齡的例子

16,16,16,17,17, 18, 18, 19, 20, 21, 21

假設 90 是一個異常值

考慮包含此異常值的資料

16,16,16,17,17, 18, 18, 19, 20, 21, 90

我們將得到平均值為 16+16+16+17+17+18+18+19+20+21+90=268/11 = 24.36，這與 18.03 大相徑庭。因此，結果將是錯誤的。

有幾種迴歸技術可以識別並從資料集中去除異常值。但是，一般來說，如果確認異常值是極端值並將其從計算中移除，則可以最大限度地減少異常值的影響。

結論

資料集的中心值在經濟學和統計學中有很多用途，因為測量中心值可以瞭解影響各種計算的中心值的頻率。因此，學習和應用非常重要。

常見問題

問題 1. 集中趨勢的度量是什麼意思？

答案。 集中趨勢的度量也稱為中心度量或中心位置度量，是指試圖用單個值來表示整個資料集的彙總度量，該值顯示分佈的中心值。

問題 2. 集中趨勢的度量有哪些三種類型？

答案。 眾數、中位數和平均數是集中趨勢的三種度量。

問題 3. 哪種集中趨勢的度量是資料的算術平均值？

答案。 平均數是資料集的算術平均值。