資料結構
網路
關係資料庫管理系統(RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝學
法學研究心理學中的集中趨勢度量
在心理學中，“集中趨勢”指的是資料集的中間部分或分數傾向於下降的部分。集中趨勢可以用均值、中位數和眾數來衡量。這些指標結合起來，可以提供資料的完整畫面。根據特定資料集的分佈情況，某些集中趨勢度量比其他度量更適用。如果數字聚集在預期分數範圍的中間，則均值是資料的最佳表示。當值分組在一個數據範圍的一端，而在另一端發現異常值時，中位數更好地代表資料。當研究人員進行心理學實驗時，會產生大量原始資料。這些資料通常被安排成兩組分數，必須比較這兩組分數以檢視它們之間是否存在明顯的差異。研究人員通常需要描述這些資訊，以便其他人能夠快速判斷該研究是否有效。
什麼是集中趨勢度量？
一組定義典型分數的示例被稱為集中趨勢度量。心理學中使用的三種集中趨勢度量是均值、中位數和眾數。這些度量旨在用單個數字來表示整個資料集。如果直方圖準確地描繪了資料的對稱分佈，則均值、中位數和眾數都將顯示相同的值。然而，由於經常看到不對稱資料分佈，不同的情況可能需要不同的方法。這種區別源於每個度量揭示了它是如何計算和定義的。
主要有三種集中趨勢度量。簡而言之，它們可以解釋如下：
均值 - 它是樣本資料的平均分數。
中位數 - 在分數按數值順序排列後，中間分數定義為中位數。
眾數 - 它定義為出現頻率最高的數值。
讓我們分別詳細討論每一個：
均值 - 給定資料集中平均值是指“均值”。它是透過將所有分數相加並將其結果除以總數來計算的。在圖表上，均值將位於總分數的中間。均值是最著名的集中趨勢度量，也是最佳分數預測器。均值與準確性有關，並且與樣本和總體相關。只有當資料處於區間水平時才能使用均值。對總體的典型樣本是準確性的一個問題。
此外，異常值或極端資料點可能會影響均值。資料表中比資料集中的其餘值高得多或低得多的數字稱為異常值。因為它是一個分散於其他資料點的點，所以資料集中存在異常值的可能性會增加樣本均值被扭曲的可能性。在這種情況下，均值將不是可靠的預測資料行為的指標，而另一種集中趨勢度量可能是一個更好的選擇。大多數研究人員必須使用樣本，並且嘗試比較與研究人員感興趣的總體密切相關的均值。
優點 - 均值可以被視為對一組分數均值的精確和靈敏的度量，這就是為什麼均值考慮資料集的所有分數的原因。
缺點 - 使用均值的一個缺點是它可能會受到資料集異常分數的影響。
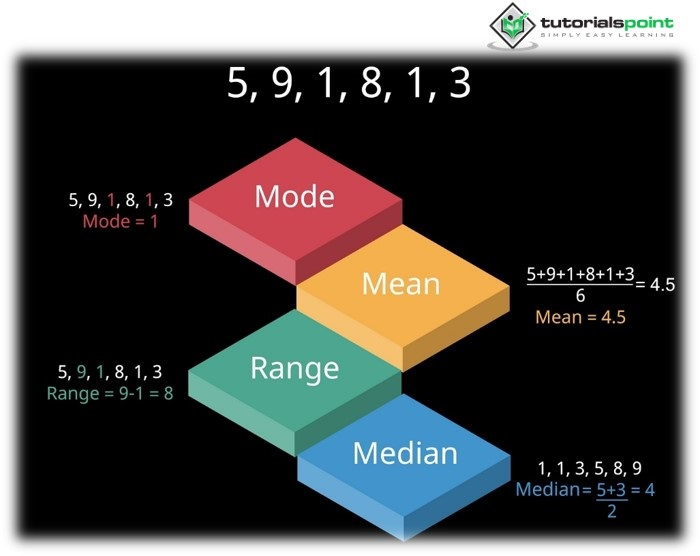
中位數 - 中位數是資料集的中間分數。它是透過按數值順序排列所有分數來計算的，然後指出中間值。如果分數的數量是偶數，則將其平均以找到中位數。只有當資料至少達到順序水平時，才使用中位數。
優點 - 使用中位數作為集中趨勢度量的一個優點是它不會受到異常值或異常分數的影響。
缺點 - 使用中位數的一個缺點是它沒有考慮資料集中所有分數。因此，中位數的精確性很容易受到質疑。
眾數 - 原始資料集中出現次數最多的分數稱為眾數。由於眾數只需要名義資料，因此它可以用於任何級別的資料。
優點 - 使用眾數的優點是極端值或異常分數不會影響它。
缺點 - 它沒有考慮資料集中所有分數。
使用集中趨勢度量的原因
研究人員使用每個指標來理解樣本並識別樣本作為總體的代表。總體是指可以研究的整個群體。同時，樣本只不過是從特定總體中選擇的樣本。一個好的樣本可以代表總體。一個可以指定精確分數的度量，例如集中趨勢，在心理學中非常有用，因為它使研究人員能夠識別最可能發生的事件。此外，它可以幫助研究人員更準確地估計特定群體的正常情況。這些度量將幫助心理學家準備對透過研究積累的資料的理解。
結論
上述推理得出結論，當結合使用心理學統計資料時，會使用三種集中趨勢度量：均值、中位數和眾數。集中趨勢的度量有助於確定資料集的中間分數或平均值。
2K+瀏覽量
