資料結構
網路
關係資料庫管理系統(RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
服裝學
法學設△ABC的頂點為A(4, 2), B(6,5) 和 C(1, 4)。
(i) 從A點引出的中線交BC於D點。求D點的座標。
(ii) 求AD上一點P的座標，使得AP : PD = 2 : 1。
(iii) 分別求中線BE和CF上點Q和R的座標，使得BQ : QE = 2 : 1且CR : RF = 2 : 1。
(iv) 你觀察到了什麼？
[注：三條中線交於一點，該點稱為三角形的重心，該點將每條中線分成2:1的比例]
(v) 如果△ABC的頂點為A(x₁, y₁), B(x₂, y₂) 和 C(x₃, y₃)，求該三角形重心的座標。
待辦事項
我們需要求解
(i) D點的座標。
(ii) 求AD上一點P的座標，使得AP : PD = 2 : 1。
(iii) 分別求中線BE和CF上點Q和R的座標，使得BQ : QE = 2 : 1且CR : RF = 2 : 1。
(iv) 我們觀察到什麼
[注：三條中線交於一點，該點稱為三角形的重心，該點將每條中線分成2:1的比例]
(v) 如果△ABC的頂點為A(x₁, y₁), B(x₂, y₂) 和 C(x₃, y₃)，求該三角形重心的座標。
解答
(i) D是BC的中點。
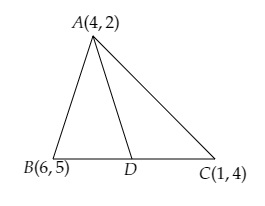
這意味著：
利用中點公式，我們得到：
D的座標為( (6+1)/2, (5+4)/2 )
= (7/2, 9/2)
D點的座標為(7/2, 9/2)。
(ii) D是BC的中點。
這意味著：
利用中點公式，我們得到：
D的座標為( (6+1)/2, (5+4)/2 )
= (7/2, 9/2)
AP : PD = 2 : 1。
利用分點公式，我們得到：
(x,y) = ( (mx₂ + nx₁)/(m+n), (my₂ + ny₁)/(m+n) )
P的座標為( (2 × 7/2 + 1 × 4)/(1+2), (2 × 9/2 + 1 × 2)/(1+2) )
= ( (7+4)/3, (9+2)/3 )
= (11/3, 11/3)
P的座標為(11/3, 11/3)。
(iii) D是BC的中點。
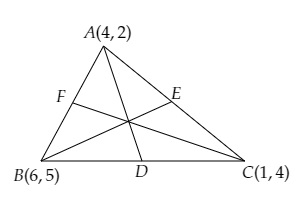
這意味著：
利用中點公式，我們得到：
D的座標為( (6+1)/2, (5+4)/2 )
= (7/2, 9/2)
同樣地：
E的座標為( (4+1)/2, (2+4)/2 )
= (5/2, 3)
F的座標為( (4+6)/2, (2+5)/2 )
= (5, 7/2)
AP : PD = 2 : 1。
利用分點公式，我們得到：
(x,y) = ( (mx₂ + nx₁)/(m+n), (my₂ + ny₁)/(m+n) )
P的座標為( (2 × 7/2 + 1 × 4)/(1+2), (2 × 9/2 + 1 × 2)/(1+2) )
= ( (7+4)/3, (9+2)/3 )
= (11/3, 11/3)
BQ : QE = 2 : 1
Q的座標為( (2 × 5/2 + 1 × 6)/(1+2), (2 × 3 + 1 × 5)/(1+2) )
= ( (5+6)/3, (6+5)/3 )
= (11/3, 11/3)
CR : RF = 2 : 1
R的座標為( (2 × 5 + 1 × 1)/(1+2), (2 × 7/2 + 1 × 4)/(1+2) )
= ( (10+1)/3, (7+4)/3 )
= (11/3, 11/3)
我們觀察到P、Q和R的座標相同。P、Q和R重合。
三角形三條中線交於同一點，該點稱為三角形的重心。
因此，(11/3, 11/3)是三角形ABC的重心。
Q和R的座標為(11/3, 11/3)。
(iv) 由於P、Q和R的座標為(11/3, 11/3)，這表明P、Q和R的中線交於△ABC的重心。
(v)
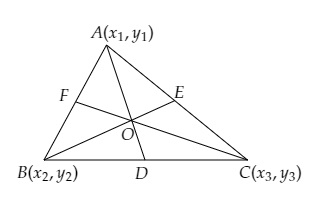
我們知道：
三角形重心的座標為( (橫座標之和)/3, (縱座標之和)/3 )
因此：
三角形ABC重心的座標為：
( (x₁+x₂+x₃)/3, (y₁+y₂+y₃)/3 )
三角形ABC重心的座標為( (x₁+x₂+x₃)/3, (y₁+y₂+y₃)/3 )。
同樣地：
頂點為A(4, 2), B(6,5) 和 C(1, 4)的三角形ABC的重心座標為
( (4+6+1)/3, (2+5+4)/3 ) = (11/3, 11/3)
瀏覽量：50
