資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究在給定圖形中，ABC 和 DBC 是同底 BC 上的兩個三角形。如果 AD 與 BC 相交於 O，證明：\( \frac{\operatorname{ar}(\triangle \mathbf{A B C})}{\operatorname{ar}(\triangle \mathbf{D B C})}=\frac{\mathbf{A O}}{\mathbf{D O}} \)
"
已知
ABC 和 DBC 是同底 BC 上的兩個三角形。
AD 與 BC 相交於 O
要求
我們必須證明：\( \frac{\operatorname{ar}(\triangle \mathbf{A B C})}{\operatorname{ar}(\triangle \mathbf{D B C})}=\frac{\mathbf{A O}}{\mathbf{D O}} \)
解答
作 AM⊥BC 和 DN⊥BC
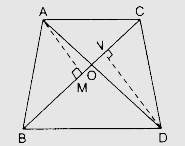
在△AOM 和△DON 中，
∠AOM = ∠DON (對頂角)
∠AMO = ∠DNO = 90°
因此，根據 AA 相似性，
△AOM ∽ △DON
這意味著，
\( \frac{\mathrm{AM}}{\mathrm{DN}}=\frac{\mathrm{AO}}{\mathrm{DO}} \) (對應邊成比例)
因此，
\( \frac{\operatorname{ar} \Delta \mathrm{ABC}}{\operatorname{ar} \Delta \mathrm{DBC}}=\frac{\frac{1}{2} \times \mathrm{BC} \times \mathrm{AM}}{\frac{1}{2} \times \mathrm{BC} \times \mathrm{DN}} \)
= \( \frac{\mathrm{AM}}{\mathrm{DN}} \)
\( \frac{\operatorname{ar} \triangle \mathrm{ABC}}{\operatorname{ar} \triangle \mathrm{DBC}}=\frac{\mathrm{AO}}{\mathrm{DO}} \) (因為 \( \frac{\mathrm{AM}}{\mathrm{DN}}=\frac{\mathrm{AO}}{\mathrm{DO}} \) )
證畢。
51 次瀏覽
