亨德森-哈塞爾巴爾赫方程

---

引言

亨德森-哈塞爾巴爾赫方程由Lawrence Joseph Henderson於1908年推導得出。該方程用於計算緩衝溶液的pH值。Karl Albert Hasselbalch於1917年將該方程改寫為對數形式。該方程的對數形式更為常用。緩衝溶液是由酸和鹽組成的混合物。緩衝溶液的特性是，即使新增酸或鹼，緩衝混合物的pH值也不會發生變化。

也就是說，它們具有抵抗pH值變化的能力。計算氫離子濃度從而檢查緩衝溶液的酸度是比較困難的。但是，亨德森-哈塞爾巴爾赫方程的出現使這一過程變得容易。

什麼是亨德森-哈塞爾巴爾赫方程？

亨德森-哈塞爾巴爾赫方程是酸鹼化學中一個重要的方程，可用於計算緩衝溶液的pH值。緩衝溶液對pH值的變化具有很強的抵抗力。緩衝溶液始終具有恆定的氫離子濃度，並且不會隨著鹼或酸的新增而改變。該方程給出了酸溶液的pH值與其相應的酸解離常數之間的關係，從而可以計算緩衝溶液的pH值。方程為：

$$\mathrm{pH\:=\:pKa\:+\:\log\:([共軛鹼]/[弱酸])}$$

$$\mathrm{pH\:=\:pKa\:+\:\log[A^{-}]/[HA]}$$

上述術語中，[HA]是弱酸的濃度，[𝐴−]是由質子損失形成的共軛鹼的濃度。使用該方程只能計算pH值的近似值。該值並非精確值，會存在少量偏差。無法計算強酸和強鹼的pH值。該方程的主要優點在於，由於緩衝溶液對pH值變化的抵抗力，計算其pH值是不可能的，並且它們在稀釋時也不會受到干擾，但藉助該方程，這已成為可能。它通常被稱為亨德森方程。

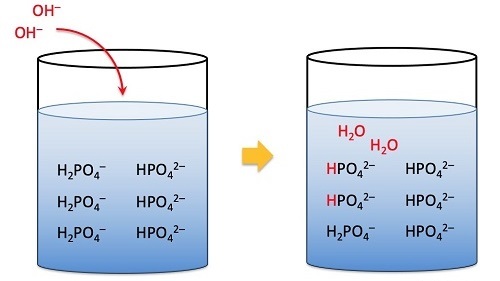
亨德森-哈塞爾巴爾赫方程的理論

化學家和生物學家利用亨德森-哈塞爾巴爾赫方程估算緩衝溶液的pH值。

• 該方程給出了溶液的pH和pOH以及pKa和pKb之間的適當關係。

• 首先利用該方程確定血液中碳酸氫鹽緩衝系統的pH值。

• 這是一種動力學分析，有助於計算緩衝溶液的酸度，而這在以前被認為是不可能的。

• 它是酸鹼化學中的一個重要方程。

• 它甚至用於計算製備相應緩衝溶液所需的pH值。

亨德森-哈塞爾巴爾赫方程的應用

該方程有很多應用。下面指出一些重要的應用。

• 它可以利用不同溶液的pKa值來計算pH值。

• 該方程可用於計算未解離和解離化學物質的濃度。

• 可以利用pH值計算溶液的pKa值。

• 可以利用從方程獲得的pH值來計算溶解度。

• 利用該方程計算蛋白質的等電點。

• 它用於確定生物分子的質子化狀態。

關於亨德森-哈塞爾巴爾赫方程的更多資訊

亨德森-哈塞爾巴爾赫方程還具有一些其他特性，例如：

• 該方程可用於確定向緩衝液中新增少量酸或鹼時緩衝溶液的pH值的影響。

• 該方程還描述了緩衝溶液。

• 它還將描述共軛酸和鹼的相對強度。

• 該方程是酸鹼化學領域的一項突破，因為它可以計算緩衝溶液的pH值。

亨德森-哈塞爾巴爾赫方程的推導

以弱酸HA的解離為例，可以推匯出亨德森-哈塞爾巴爾赫方程。解離過程為：

$$\mathrm{HA\:+\:H_{2}O\:\leftrightarrows\:A^{-}\:+\:H_{3}O^{+}}$$

然後，可以計算解離常數Ka為：

$$\mathrm{Ka\:=\:[A^{-}][H_{3}O^{+}]/[HA]}$$

$$\mathrm{Ka[HA]/[A^{-}]\:=\:[H_{3}O^{+}]}$$

$$\mathrm{[H_{3}O^{+}]\:=\:Ka[HA]/[A^{-}]}$$

對等式兩邊取對數。方程變為：

$$\mathrm{\log\:[H_{3}O^{+}]\:=\:\log\:Ka\:+\:\log\:[HA]/[A^{-}]}$$

將上述方程乘以-1，將得到：

$$\mathrm{-\log\:[H_{3}O^{+}]\:=\:-\log\:Ka\:-\:\log\:[HA]/[A^{-}]}$$

已知：

$\mathrm{pH\:=\:-\log\:[H_{3}O^{+}]}$

以及 $\mathrm{pKa\:=\:-\log\:Ka}$

因此，將這些值代入上述方程，得到：

$$\mathrm{pH\:=\:pKa\:+\:\log\:[A^{-}]/[HA]}$$

這就是亨德森-哈塞爾巴爾赫方程。它用於估算緩衝溶液的pH值。當酸和共軛鹼的濃度相同時，pH和pKa相等。也就是說：

$$\mathrm{[HA]\:=\:[A^{-}]}$$

所以，$\mathrm{[A^{-}]/[HA]\:=\:1}$

因此，亨德森-哈塞爾巴爾赫方程變為：

$$\mathrm{pH\:=\:pKa\:+\:\log\:1}$$

也就是說：

$$\mathrm{pH\:=\:pKa}$$

這是從亨德森-哈塞爾巴爾赫方程獲得的另一個數學關係，可用於計算化學化合物的pKa值。

結論

亨德森-哈塞爾巴爾赫方程是化學（酸鹼化學）分支中的重要方程之一。幾年前，計算緩衝溶液的pH值是不可能的。但隨著該方程的出現，這已成為可能。該方程的形式最常用於計算緩衝溶液的pH值。該方程說明了pH和pKa之間的關係。它不僅可以計算緩衝液的pH值，還可以用於其他應用，例如濃度計算、pKa值計算等。它是藉助弱酸情況下的pH值計算推匯出來的。方程為：$\mathrm{pH\:=\:pKa\:+\:\log\:[A^{-}]/[HA]}$。

常見問題

1. 亨德森-哈塞爾巴爾赫方程的侷限性是什麼？

由於該方程未考慮水的自解離，因此無法利用該方程確定極稀溶液的緩衝溶液。此外，它不適用於強酸和強鹼。

2. 體積在亨德森-哈塞爾巴爾赫方程中重要嗎？

亨德森-哈塞爾巴爾赫方程只考慮酸和共軛鹼的濃度。因此，該方程與體積無關。

3. 為什麼緩衝容量很重要？

緩衝容量是與緩衝溶液相關的術語，它是緩衝溶液抵抗pH值變化的能力。這意味著緩衝液如何抵抗透過新增𝐻+或𝑂𝐻−離子而不會發生任何pH值變化。

4. 為什麼稀釋緩衝液不會改變pH值？

緩衝液的pH值取決於Ka和Kb值，而這些值不會隨pH值的變化而變化。此外，酸和鹽的濃度也不會改變，因此pH值不會隨稀釋而改變。

5. 緩衝液的例子有哪些？

緩衝液的例子包括碳酸和碳酸氫根離子、檸檬酸和檸檬酸鈉、乙酸和乙酸鈉等。