相消干涉方程

---

介紹

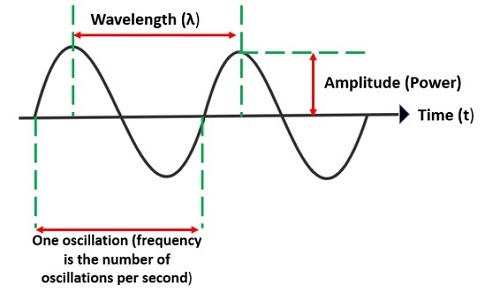
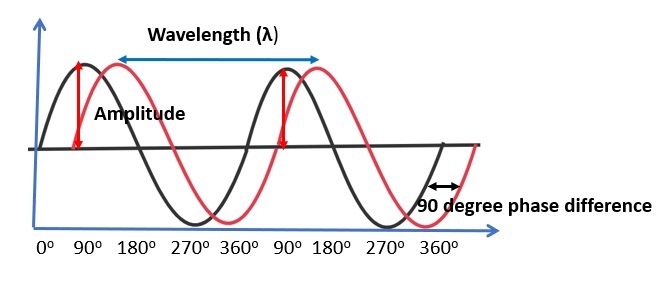
相消干涉是基於波疊加的概念。波是在介質中傳播能量而不傳播質量的擾動。波通常處於週期性運動中，就像一個簡單的諧振子。它們有波峰和波谷。波的振幅是波的高度。兩個連續波峰之間所覆蓋的距離稱為波長。每秒鐘經過的波數稱為波的頻率。相位不是波的屬性，但它給出了兩個具有相同頻率的訊號之間的關係。粒子是一個局域化的物體，它擁有物理和化學性質，例如體積、質量、密度等。它們的大小可能不同，例如亞原子粒子、微觀粒子和大塊物質。

什麼是波的干涉？

干涉是波疊加的現象。當兩列波在同一介質中傳播時，它們會相互干涉，這被稱為波的干涉。當兩列波疊加時，它們的振幅在每個點上都會相加，形成一個合波。合波可能具有較低、較高或相同的振幅。干涉效應適用於不同的波，例如光波、無線電波、聲波和水波。波的干涉分為兩種型別：相長干涉和相消干涉。

什麼是相消干涉？

當兩列即將相互作用的波的波峰相位差為180度時，一列波的位移為正，另一列波的位移為負。因此，在相互作用過程中，每列波的位移相互抵消。當第一列波的振幅上升時，第二列波的振幅下降，反之亦然。由於兩列波的振幅在每個點上相互抵消，因此合波實際上沒有波。

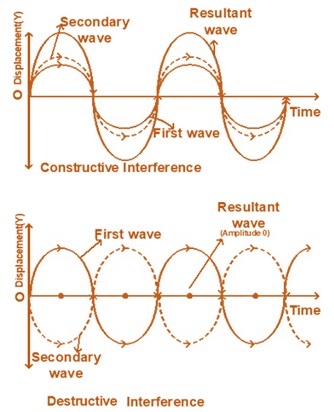
干涉最重要的條件至少是出現兩列波。具有相同振幅和頻率的波可以疊加併發生干涉。如果兩列頻率相當的波相互疊加，則合波的強度不同於總強度。合波的強度在不同的點上是不同的。

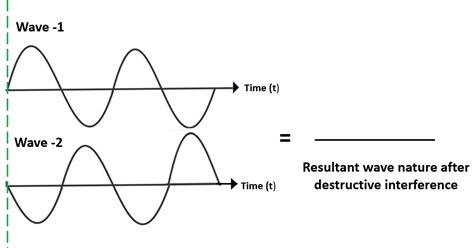
相消干涉方程

兩列波之間的干涉可以用下面的數學公式表示。讓我們考慮兩列在同一介質中具有相同振幅的波。沿正X方向傳播的波的方程為：

$$\mathrm{Y_1=Acos(kx-\omega t)}$$

其中A表示振幅

k表示波數，$\mathrm{k=\frac{2π}{λ}}$

λ表示波長。

ω表示角頻率，ω=2πf

讓我們取第二列波，它具有一定的相位差，並具有相同的振幅和頻率。第二列波的方程為：

$$\mathrm{Y_2=Acos(kx-\omega t+\varphi)}$$

疊加時，振幅相加。

$$\mathrm{Y_1+Y_2=Acos(kx-\omega t)+Acos(kx-\omega t+\varphi)}$$

$$\mathrm{ Y_1+Y_2=A[cos(kx-\omega t)+cos(kx-\omega t+\varphi)]}$$

$$\mathrm{cos A +cos B=2cos(\frac{A-B}{2})cos(\frac{A+B}{2})}$$

所以，

$$\mathrm{Y_1+Y_2=2A[cos(\frac{kx-\omega t-kx+\omega t+\varphi}{2}) cos(\frac{kx-\omega t+kx-\omega t+\varphi}{2})]}$$

$$\mathrm{Y_1+Y_2=2A[cos(\frac{φ}{2}) cos(kx-ωt-\frac{φ}{2})]}$$

相長干涉

對於相長干涉，相位差是π的偶數倍。φ=0, 2π, 4π 等。所以$\mathrm{cos(\frac{φ}{2})=1}$。合波的振幅加倍。

$$\mathrm{Y_1+Y_2=2A cos(kx-\omega t)}$$

相消干涉

對於相消干涉，相位差是π的奇數倍。φ=π, 3π, 5π 等。所以$\mathrm{cos(\frac{φ}{2})=0}$。合波的振幅為零。

相消干涉的例子

下面給出一些相消干涉的例子。

• 運動的電子和無線電波也會導致相消干涉。對於運動的電子來說，相消干涉很容易發生，並且可以遵循相消干涉規則。

• 在降噪耳機中，相消干涉是一個重要因素。由於播放聲音時聲波的振幅方向相反，因此會發生相消干涉，它們相互抵消，從而降低噪音。

• 引力波就是一個相消干涉的例子。由於引力波在不同地點的傳播速度不同，因此很難找到參考系。這就是在那裡發生相消干涉的原因。

• 光束也是相消干涉的例子。

• 汽車消聲器也是相消干涉的例子。通常也稱為消音器。因此，它安裝在任何車輛上以消除噪音。

• 大多數樂器都是相消干涉的例子。

• 揚聲器波也會發生相消干涉。

結論

介質中傳遞能量的擾動稱為波。衍射、干涉和偏振等現象表明光表現得像波。當兩列波疊加時，它們會形成干涉波。根據疊加方式，波的干涉分為兩種：相消干涉和相長干涉。當兩列相同振幅的波相位差為180度時，它們的相反振幅相互抵消，合波的振幅為零。本教程還詳細討論了相消干涉方程及其一些例子。

常見問題

1.波的特性是什麼？

波的特性如下。

• 振幅 - 粒子在波中從平均位置所做的最大位移。

• 週期 - 波完成一次往復運動所需的時間。

• 波長 - 兩個連續波峰或波谷之間的距離。

• 頻率 - 每秒鐘完成的往復運動次數。

• 速度 - 波每秒傳播的距離。

2.什麼是相長干涉？

如果兩列波的波峰同相，則兩列波的位移都為正或都為負。因此，在兩列這樣的波相互作用過程中，兩列波的振幅相加，合波的振幅是兩列波振幅之和。這被稱為相長干涉。

3.什麼是波數？

在光譜學中，波數定義為單位距離內的波數。它被稱為空間波數，其測量單位為cm^-1。在理論物理學中，波數定義為單位距離記憶體在的弧度數。它被稱為角波數。它表示為：

$$\mathrm{ k=\frac{2π}{λ}}$$

4.在相消干涉過程中會發生什麼，它們的相位差和路程差是多少？

在相消干涉過程中，兩列波以相互抵消的方式疊加。兩列波的相位差是π的奇數倍。

$$\mathrm{波之間的相位差\: =\phi= (2n-1) \pi}$$

兩列波的路程差是λ/2的奇數倍。

$$\mathrm{波之間的路程差\: =\Delta= (2n-1) λ/2.}$$

5.什麼是波的疊加原理？

疊加原理也稱為疊加特性。當兩列波在同一平面內傳播時，它們會發生疊加，合波的振幅是兩列個體波的振幅之和。