
- 電子電路資源
- 電子電路 - 快速指南
- 電子電路 - 資源
- 電子電路 - 討論
低通濾波器和高通濾波器的特殊功能
低通濾波器 (LPF) 和高通濾波器 (HPF) 電路在許多應用中用作特殊電路。低通濾波器 (LPF) 可以作為積分器工作,而高通濾波器 (HPF) 可以作為微分器工作。只有這些電路才能實現這兩個數學函式,從而減少了電子工程師在許多應用中的工作量。
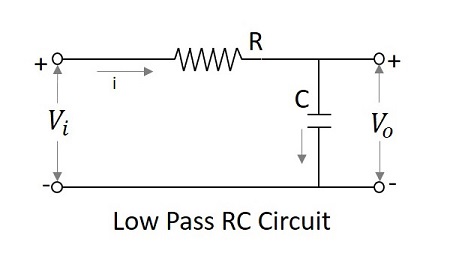
低通濾波器作為積分器
在低頻下,容抗趨於無窮大,在高頻下容抗趨於零。因此,在低頻下,LPF 有有限的輸出,在高頻下輸出為零,這與積分器電路相同。因此,可以說低通濾波器可以作為積分器工作。
為了使 LPF 充當積分器
$$τ >> T$$
其中 $τ = RC$ 為電路的時間常數
則 C 上的電壓變化非常小。
$$V_{i}=iR+\frac{1}{C} \int i \:dt$$
$$V_{i}\cong iR$$
$$因為 \:\: \frac{1}{C} \int i \:dt << iR$$
$$i=\frac{V_{i}}{R}$$
$$ 因為 \:\: V_{0}=\frac{1}{C}\int i dt =\frac{1}{RC}\int V_{i}dt=\frac{1}{\tau }\int V_{i} dt$$
$$輸出 \propto \int 輸入$$
因此,具有大時間常數的 LPF 會產生與輸入積分成正比的輸出。
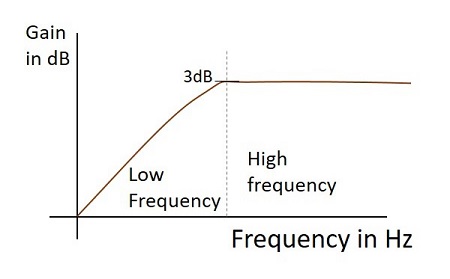
頻率響應
當實際低通濾波器作為積分器工作時的頻率響應如下所示。

輸出波形
如果給積分器電路一個正弦波輸入,則輸出將是餘弦波。如果輸入是方波,則輸出波形的形狀會發生變化,如下面的圖所示。

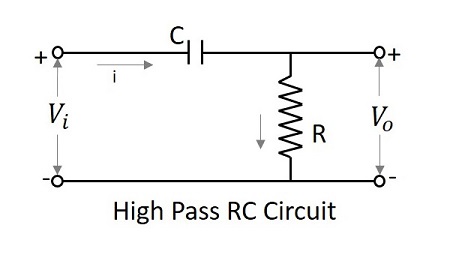
高通濾波器作為微分器
在低頻下,微分器的輸出為零,而在高頻下,其輸出為某個有限值。這與微分器相同。因此,據說高通濾波器充當微分器。
如果 RC 高通濾波器的時間常數遠小於輸入訊號的週期,則電路表現為微分器。然後,與跨 C 的壓降相比,跨 R 的壓降非常小。
$$V_{i}=\frac{1}{C}\int i \:dt +iR$$
但 $iR=V_{0}$ 很小
$$因為 V_{i}=\frac{1}{C}\int i \:dt$$
$$i=\frac{V_{0}}{R}$$
$$因為 \: V_{i} =\frac{1}{\tau }\int V_{0} \:dt$$
其中 $τ =RC$ 為電路的時間常數。
兩邊求導,
$$\frac{dV_{i}}{dt}=\frac{V_0}{\tau }$$
$$V_{0}=\tau \frac{dV_{i}}{dt}$$
$$因為 \:V_{0}\propto \frac{dV_{i}}{dt}$$
輸出與輸入訊號的微分成正比。
頻率響應
當實際高通濾波器作為微分器工作時的頻率響應如下所示。
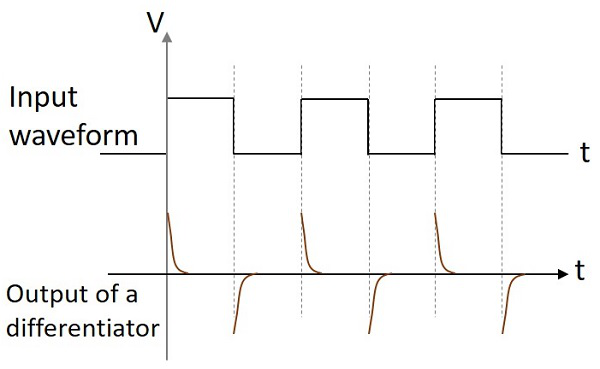
輸出波形
如果給微分器電路一個正弦波輸入,則輸出將是餘弦波。如果輸入是方波,則輸出波形的形狀會發生變化,如下面的圖所示。
這兩個電路主要用於各種電子應用中。當輸入電壓穩定變化時,微分器電路產生恆定的輸出電壓。當施加的輸入電壓恆定時,積分器電路產生穩定變化的輸出電壓。