
- 電子電路資源
- 電子電路 - 快速指南
- 電子電路 - 資源
- 電子電路 - 討論
電子電路 - 快速指南
電子電路 - 簡介
在電子學中,我們有不同的元器件,它們服務於不同的目的。有各種各樣的元件被用於許多型別的電路,具體取決於應用。
電子元器件
類似於構建牆壁的磚塊,元器件是電路的基本組成部分。元器件是基本元素,有助於將一個想法發展成一個用於執行的電路。
每個元器件都具有一些基本特性,並且元器件的行為也隨之變化。這取決於開發人員的目標,以利用它們來構建預期的電路。下圖顯示了一些用於不同電子電路中的電子元器件示例。

為了獲得一個概念,讓我們看看元器件的型別。它們可以是有源元器件或無源元器件。
有源元器件
有源元器件是在提供一些外部能量後才能導通的元器件。
有源元器件以電壓或電流的形式產生能量。
示例 - 二極體、電晶體、變壓器等。
無源元器件
無源元器件是連線後即可開始工作的元器件。它們的工作不需要外部能量。
無源元器件以電壓或電流的形式儲存和維持能量。
示例 - 電阻器、電容器、電感器等。
我們還有另一種分類,即線性和非線性元件。
線性元件
線性元件或元件是電流和電壓之間存線上性關係的元件。
線性元件的引數不會隨電流和電壓而變化。
示例 - 二極體、電晶體、變壓器等。
非線性元件
非線性元件或元件是電流和電壓之間存在非線性關係的元件。
非線性元件的引數會隨電流和電壓而變化。
示例 - 電阻器、電容器、電感器等。
這些元件用於各種目的,它們組合在一起可以執行為其構建的首選任務。這種不同元件的組合稱為電路。
電子電路
當一定數量的元件以特定方式連線在一個特定目的上時,就形成了一個電路。電路是不同元件的網路。電路有不同的型別。
下圖顯示了不同型別的電子電路。它顯示了印刷電路板,印刷電路板是一組連線在電路板上的電子電路。

電子電路可以根據其工作原理、連線方式、結構等分為不同的類別。讓我們進一步討論電子電路的型別。
有源電路
使用有源元件構建的電路稱為有源電路。
它通常包含一個電源,電路從中提取更多功率並將其傳遞到負載。
輸出增加了額外的功率,因此輸出功率始終大於施加的輸入功率。
功率增益始終大於1。
無源電路
使用無源元件構建的電路稱為無源電路。
即使它包含一個電源,電路也不會提取任何功率。
輸出沒有增加額外的功率,因此輸出功率始終小於施加的輸入功率。
功率增益始終小於1。
電子電路還可以分類為模擬、數字或混合。
類比電路
類比電路可以是其中包含線性元件的電路。因此,它是一個線性電路。
類比電路具有模擬訊號輸入,這些輸入是連續範圍的電壓。
數位電路
數位電路可以是其中包含非線性元件的電路。因此,它是一個非線性電路。
它只能處理數字訊號。
數位電路具有數字訊號輸入,這些輸入是離散值。
混合訊號電路
混合訊號電路可以是同時包含線性元件和非線性元件的電路。因此,它被稱為混合訊號電路。
這些電路由類比電路以及用於處理輸入的微處理器組成。
根據連線型別,電路可以分類為串聯電路或並聯電路。串聯電路是指串聯連線的電路,並聯電路是指其元件並聯連線的電路。
現在我們對電子元器件有了基本的瞭解,讓我們繼續討論它們的用途,這將有助於我們為不同的應用構建更好的電路。無論電子電路的目的是什麼(處理、傳送、接收、分析),處理過程都以訊號的形式進行。在下一章中,我們將討論訊號以及電子電路中存在的訊號型別。
電子電路 - 訊號
訊號可以理解為“表示從產生它的源頭存在的關於資料的某些資訊”。這通常是隨時間變化的。因此,訊號可以是傳輸某些資訊的能量源。這很容易在圖表上表示。
示例
- 鬧鐘發出訊號表示該起床了。
- 高壓鍋的哨聲確認食物已煮熟。
- 紅燈表示某些危險。
- 交通訊號指示你的通行。
- 電話鈴響表示有人給你打電話。
訊號可以是任何型別的傳遞資訊的訊號。從電子裝置產生的這種訊號稱為電子訊號或電訊號。這些通常是隨時間變化的。
訊號型別
訊號可以根據其特性分為模擬訊號和數字訊號。模擬訊號和數字訊號可以進一步分類,如下面的圖片所示。

模擬訊號
表示隨時間變化的量的連續時間變化訊號可以稱為模擬訊號。該訊號會根據表示它的量的瞬時值隨時間變化。
數字訊號
本質上是離散的或形式上是非連續的訊號可以稱為數字訊號。該訊號具有單獨表示的各個值,這些值不基於先前值,就像它們是在該特定時間瞬間匯出的。
週期訊號和非週期訊號
任何在一段時間內重複其模式的模擬或數字訊號都稱為週期訊號。該訊號的模式重複繼續,並且易於假設或計算。
任何在一段時間內不重複其模式的模擬或數字訊號都稱為非週期訊號。該訊號的模式繼續,但模式不重複,因此不容易假設或計算。
訊號和符號
在週期訊號中,最常用的訊號是正弦波、餘弦波、三角波、方波、矩形波、鋸齒波、脈衝波或脈衝序列等。讓我們看一下這些波形。
單位階躍訊號
單位階躍訊號從其原點到 X 軸上的一個單位具有一個單位的值。這主要用作測試訊號。單位階躍訊號的影像如下所示。

單位階躍函式用 $u\left ( t \right )$ 表示。其定義如下:
$$u\left ( t \right )=\left\{\begin{matrix}1 & t\geq 0\\ 0 & t< 0\end{matrix}\right.$$
單位脈衝訊號
單位脈衝訊號在其原點具有一個單位的值。其面積為一個單位。單位脈衝訊號的影像如下所示。

單位脈衝函式用 ẟ(t) 表示。其定義如下:
$$\delta \left ( t \right )=\left\{\begin{matrix} \infty \:\:if \:\:t=0\\0 \:\:if \:\:t\neq 0\end{matrix}\right.$$
$$\int_{-\infty }^{\infty }\delta \left ( t \right )d\left ( t \right )=1$$
$$\int_{-\infty }^{t }\delta \left ( t \right )d\left ( t \right )=u\left ( t \right )$$
$$\delta \left ( t \right )=\frac{du\left ( t \right )}{d\left ( t \right )} $$
單位斜坡訊號
單位斜坡訊號的值從其原點呈指數增長。單位斜坡訊號的影像如下所示。
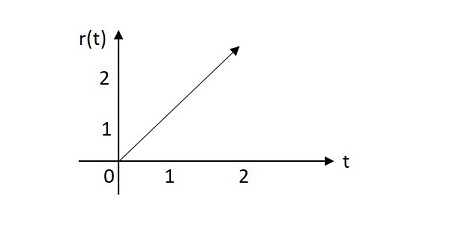
單位斜坡函式用 u(t) 表示。其定義如下:
$$\int_{0}^{t}u\left ( t \right ) d\left ( t \right )=\int_{0}^{t} 1 dt =t=r\left ( t \right )$$
$$u\left ( t \right )=\frac{dr\left ( t \right )}{dt}$$
單位拋物線訊號
單位拋物線訊號的值在其原點處像拋物線一樣變化。單位拋物線訊號的影像如下所示。

單位拋物線函式用 $u\left ( t \right )$ 表示。其定義如下:
$$\int_{0}^{t}\int_{0}^{t}u\left ( t \right )dtdt=\int_{0}^{t}r\left ( t \right )dt=\int_{0}^{t} t.dt=\frac{t^{2}}{2}dt=x\left ( t \right )$$
$$r\left ( t \right )=\frac{dx\left ( t \right )}{dt}$$
$$u\left ( t \right )=\frac{d^{2}x\left ( t \right )}{dt^{2}}$$
符號函式
Signum 函式的值在其原點兩側的正負平面內均勻分佈。Signum 函式的影像如下所示。
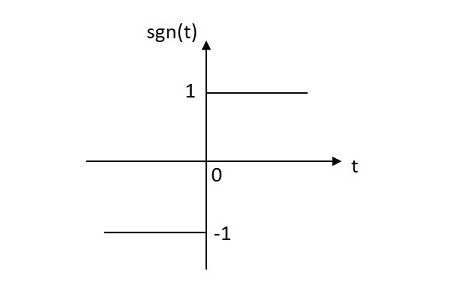
Signum 函式用sgn(t)表示。其定義如下:
$$sgn\left ( t \right )=\left\{\begin{matrix} 1 \:\: 當 \:\: t\geq 0\\-1 \:\: 當 \:\:t < 0\end{matrix}\right.$$
$$sgn\left ( t \right )=2u\left ( t \right ) -1$$
指數訊號
指數訊號的值從其原點開始呈指數變化。指數函式的形式為:
$$x\left ( t \right ) =e^{\alpha t}$$
指數函式的形狀由$\alpha$決定。此函式可以分為三種情況:
情況1 −
如果 $\alpha = 0\rightarrow x\left ( t \right )=e^{0}=1$
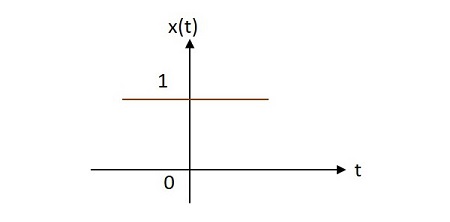
情況2 −
如果 $\alpha <0$,則 $x\left ( t \right )=e^{\alpha t}$,其中 $\alpha$ 為負數。這種形狀稱為衰減指數。

情況3 −
如果 $\alpha > 0$,則 $x\left ( t \right )=e^{\alpha t}$,其中 $\alpha$ 為正數。這種形狀稱為增長指數。
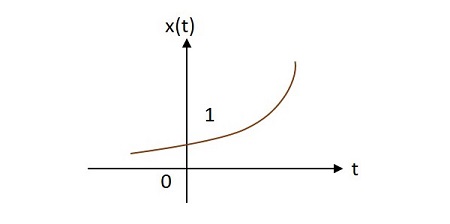
矩形訊號
矩形訊號的值在其原點兩側的正負平面內呈矩形分佈。矩形訊號的影像如下所示。

矩形函式用$x\left ( t \right )$表示。其定義如下:
$$x\left ( t \right )=A \:rect\left [ \frac{t}{T} \right ]$$
三角訊號
三角訊號的值在其原點兩側的正負平面內呈三角形分佈。三角訊號的影像如下所示。

三角函式用$x\left ( t \right )$表示。其定義如下:
$$x\left ( t \right )=A \left [ 1-\frac{\left | t \right |}{T} \right ]$$
正弦訊號
正弦訊號的值從其原點開始呈正弦變化。正弦訊號的影像如下所示。
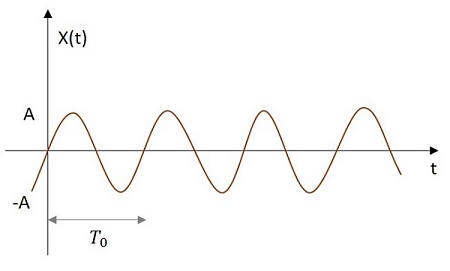
正弦函式用 x(t) 表示。其定義如下:
$$x\left ( t \right )=A \cos \left ( w_{0} t\pm \phi \right )$$
或
$$x\left ( t \right )=A sin\left ( w_{0}t\pm \phi \right )$$
其中 $T_{0}=\frac{2 \pi}{w_{0}}$
Sinc 函式
Sinc 訊號的值根據如下所示的特定關係變化。它在原點處具有最大值,並隨著遠離原點而逐漸減小。Sinc 函式訊號的影像如下所示。
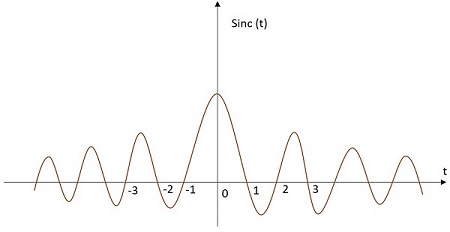
Sinc 函式用sinc(t)表示。其定義如下:
$$sinc\left ( t \right )=\frac{sin\left ( \pi t \right )}{\pi t}$$
因此,這些是在電子和通訊領域中最常遇到的不同訊號。每個訊號都可以用數學方程來定義,以使訊號分析更容易。
每個訊號都具有前面提到的特定波形。波形的形狀可能會改變訊號中存在的內容。無論如何,設計工程師是否要為了某個特定電路而改變波形,這需要做出決定。但是,要改變波形的形狀,有一些技術將在後續單元中討論。
電子電路 - 線性波形整形
訊號也可以稱為波。每種波在圖形中表示時都具有一定的形狀。這種形狀可以是多種型別,例如正弦、方波、三角波等,它們隨時間變化,或者它們可能具有與時間無關的一些隨機形狀。
波形整形的型別
波形整形主要有兩種型別。它們是:
- 線性波形整形
- 非線性波形整形
線性波形整形
在這種線性波形整形中,使用電阻器、電容器和電感器等線性元件來整形訊號。正弦波輸入具有正弦波輸出,因此非正弦輸入更常用於理解線性波形整形。
濾波是衰減不需要的訊號或再現特定訊號的頻率分量的選定部分的過程。
濾波器
在整形訊號的過程中,如果某些訊號部分被認為是不需要的,則可以使用濾波器電路將其濾除。濾波器是一種可以去除輸入訊號中不需要的部分的電路。訊號強度降低的過程也稱為衰減。
我們有一些元件可以幫助我們進行濾波技術。
電容器具有允許交流和阻擋直流的特性。
電感器具有允許直流但阻擋交流的特性。
利用這些特性,這兩個元件特別用於阻擋或允許交流或直流。濾波器可以根據這些特性進行設計。
我們有四種主要的濾波器型別:
- 低通濾波器
- 高通濾波器
- 帶通濾波器
- 帶阻濾波器
現在讓我們詳細討論這些型別的濾波器。
低通濾波器
允許一組低於指定值的頻率的濾波器電路可以稱為低通濾波器。此濾波器透過低頻。使用 RC 和 RL 的低通濾波器的電路圖如下所示。

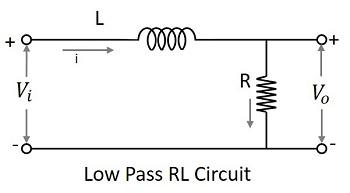
電容濾波器或RC濾波器和電感濾波器或 RL 濾波器都充當低通濾波器。
RC 濾波器 − 由於電容器並聯放置,因此它允許的交流被接地。這旁路了所有高頻分量,同時允許直流在輸出端出現。
RL 濾波器 − 由於電感器串聯放置,因此直流被允許到輸出端。電感器阻擋交流,交流不允許出現在輸出端。
低通濾波器 (LPF) 的符號如下所示。
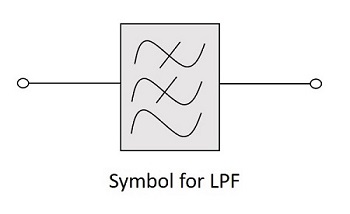
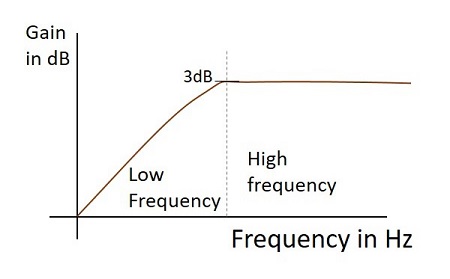
頻率響應
實際濾波器的頻率響應如下所示,並且當不考慮電子元件的實際因素時,理想 LPF 的頻率響應如下。
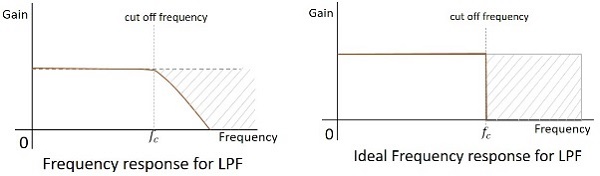
任何濾波器的截止頻率都是濾波器打算衰減(截止)訊號的關鍵頻率$f_{c}$。理想濾波器具有完美的截止,而實際濾波器則有一些限制。
RLC 濾波器
在瞭解了 RC 和 RL 濾波器之後,人們可能會想到將這兩個電路組合起來以獲得更好的響應會很好。下圖顯示了 RLC 電路的外觀。

輸入訊號透過電感器,電感器阻擋交流並允許直流。現在,該輸出再次透過並聯的電容器,如果訊號中存在任何交流分量,則將其接地,允許直流在輸出端出現。因此,我們在輸出端獲得了純直流。這比這兩個電路中的任何一個都是更好的低通電路。
高通濾波器
允許一組高於指定值的頻率的濾波器電路可以稱為高通濾波器。此濾波器透過高頻。使用 RC 和 RL 的高通濾波器的電路圖如下所示。

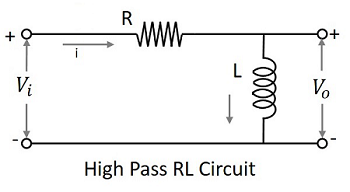
電容濾波器或RC濾波器和電感濾波器或RL濾波器都充當高通濾波器。
RC 濾波器
由於電容器串聯放置,因此它阻擋直流分量並允許交流分量到輸出端。因此,高頻分量出現在電阻器兩端的輸出端。
RL 濾波器
由於電感器並聯放置,因此直流被允許接地。剩餘的交流分量出現在輸出端。高通濾波器 (HPF) 的符號如下所示。

頻率響應
實際濾波器的頻率響應如下所示,並且當不考慮電子元件的實際因素時,理想 HPF 的頻率響應如下。

任何濾波器的截止頻率都是濾波器打算衰減(截止)訊號的關鍵頻率$f_{c}$。理想濾波器具有完美的截止,而實際濾波器則有一些限制。
RLC 濾波器
在瞭解了 RC 和 RL 濾波器之後,人們可能會想到將這兩個電路組合起來以獲得更好的響應會很好。下圖顯示了 RLC 電路的外觀。

輸入訊號透過電容器,電容器阻擋直流並允許交流。現在,該輸出再次透過並聯的電感器,如果訊號中存在任何直流分量,則將其接地,允許交流在輸出端出現。因此,我們在輸出端獲得了純交流。這比這兩個電路中的任何一個都是更好的高通電路。
帶通濾波器
允許一組兩個指定值之間的頻率的濾波器電路可以稱為帶通濾波器。此濾波器透過一個頻帶。
由於我們需要消除一些低頻和高頻,以選擇一組指定的頻率,因此我們需要級聯一個 HPF 和一個 LPF 以獲得 BPF。即使透過觀察頻率響應曲線,也可以很容易地理解這一點。
帶通濾波器的電路圖如下所示。

以上電路也可以使用 RL 電路或 RLC 電路構建。以上電路為 RC 電路,選擇用於簡單的理解。
帶通濾波器 (BPF) 的符號如下所示。

頻率響應
實際濾波器的頻率響應如下所示,並且當不考慮電子元件的實際因素時,理想 BPF 的頻率響應如下。

任何濾波器的截止頻率都是濾波器打算衰減(截止)訊號的關鍵頻率$f_{c}$。理想濾波器具有完美的截止,而實際濾波器則有一些限制。
帶阻濾波器
阻擋或衰減一組兩個指定值之間的頻率的濾波器電路可以稱為帶阻濾波器。此濾波器拒絕一個頻帶,因此也可以稱為帶阻濾波器。
由於我們需要消除一些低頻和高頻,以選擇一組指定的頻率,因此我們需要級聯一個 LPF 和一個 HPF 以獲得 BSF。即使透過觀察頻率響應曲線,也可以很容易地理解這一點。
帶阻濾波器的電路圖如下所示。

以上電路也可以使用 RL 電路或 RLC 電路構建。以上電路為 RC 電路,選擇用於簡單的理解。
帶阻濾波器 (BSF) 的符號如下所示。
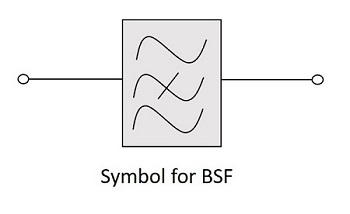
頻率響應
實際濾波器的頻率響應如下圖所示,而當不考慮電子元件的實際情況時,理想帶阻濾波器(BSF)的頻率響應如下所示。
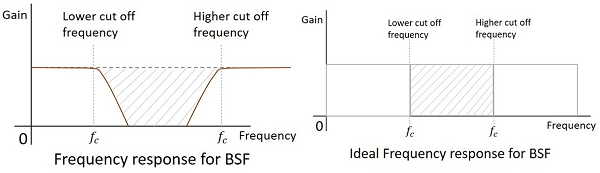
任何濾波器的截止頻率都是濾波器打算衰減(截止)訊號的關鍵頻率$f_{c}$。理想濾波器具有完美的截止,而實際濾波器則有一些限制。
低通濾波器和高通濾波器的特殊功能
低通濾波器和高通濾波器電路在許多應用中用作特殊電路。低通濾波器 (LPF) 可以作為積分器工作,而高通濾波器 (HPF) 可以作為微分器工作。只有這些電路才能實現這兩個數學函式,從而減少了電子工程師在許多應用中的工作量。
低通濾波器作為積分器
在低頻時,電容抗性趨於無窮大,而在高頻時,電容抗性變為零。因此,在低頻時,LPF 具有有限的輸出,而在高頻時,輸出為零,這與積分器電路相同。因此,可以說低通濾波器可以作為積分器工作。
為了使 LPF 充當積分器
$$\tau \gg T$$
其中 $\tau = RC$ 為電路的時間常數
然後 C 中的電壓變化非常小。
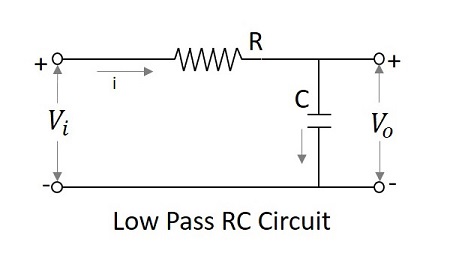
$$V_{i}=iR+\frac{1}{C} \int i \:dt$$
$$V_{i}\cong iR$$
$$因為 \:\: \frac{1}{C} \int i \:dt \ll iR$$
$$i=\frac{V_{i}}{R}$$
$$ 因為 \:\: V_{0}=\frac{1}{C}\int i dt =\frac{1}{RC}\int V_{i}dt=\frac{1}{\tau }\int V_{i} dt$$
$$輸出 \propto \int 輸入$$
因此,具有較大時間常數的 LPF 會產生與輸入積分成正比的輸出。
頻率響應
當低通濾波器作為積分器工作時,其實際頻率響應如下圖所示。

輸出波形
如果給積分器電路一個正弦波輸入,則輸出將是一個餘弦波。如果輸入是方波,則輸出波形會改變其形狀,並顯示如下面的圖形。

高通濾波器作為微分器
在低頻時,微分器的輸出為零,而在高頻時,其輸出為某個有限值。這與微分器相同。因此,可以說高通濾波器充當微分器。
如果 RC HPF 的時間常數遠小於輸入訊號的週期,則電路表現為微分器。然後,與跨 C 的壓降相比,跨 R 的壓降非常小。
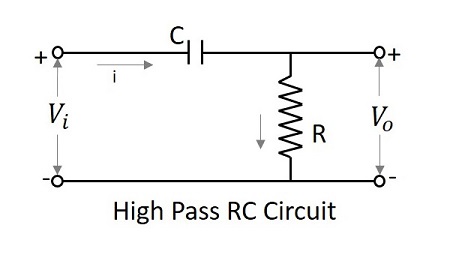
$$V_{i}=\frac{1}{C}\int i \:dt +iR$$
但 $iR=V_{0}$ 很小
$$因為 V_{i}=\frac{1}{C}\int i \:dt$$
$$i=\frac{V_{0}}{R}$$
$$因為 \: V_{i} =\frac{1}{\tau }\int V_{0} \:dt$$
其中 $\tau =RC$ 為電路的時間常數。
兩邊求導,
$$\frac{dV_{i}}{dt}=\frac{V_0}{\tau }$$
$$V_{0}=\tau \frac{dV_{i}}{dt}$$
$$因為 \:V_{0}\propto \frac{dV_{i}}{dt}$$
輸出與輸入訊號的微分成正比。
頻率響應
當高通濾波器作為微分器工作時,其實際頻率響應如下圖所示。
輸出波形
如果給微分器電路一個正弦波輸入,則輸出將是一個餘弦波。如果輸入是方波,則輸出波形會改變其形狀,並顯示如下面的圖形。
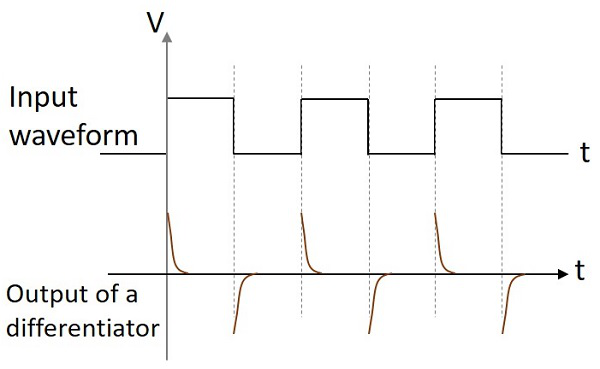
這兩種電路主要用於各種電子應用。當施加的輸入穩定變化時,微分器電路會產生恆定的輸出電壓。當施加的輸入電壓恆定時,積分器電路會產生穩定變化的輸出電壓。
非線性波形整形
除了電阻器之外,非線性波形整形電路中還使用二極體等非線性元件來獲得所需的改變後的輸出。在非線性波形整形中,要麼衰減波形的形狀,要麼改變波形的直流電平。
使用非線性元件從正弦輸入產生非正弦輸出波形的過程稱為非線性波形整形。
削波電路
削波電路是一種電路,它拒絕輸入波形中指定的部分,同時允許其餘部分透過。確定截止電壓以上或以下的波形部分會被削波或切除。
削波電路由線性元件和非線性元件(如電阻器和二極體)組成,但不包含電容器等儲能元件。這些削波電路具有許多應用,因為它們具有優勢。
削波電路的主要優點是消除幅度中存在的不需要的噪聲。
它們可以作為方波轉換器,因為它們可以透過削波將正弦波轉換為方波。
可以將所需波形的幅度保持在恆定水平。
在二極體削波器中,兩種主要型別是正削波器和負削波器。我們將在接下來的兩章中討論這兩種型別的削波器。
電子電路 - 正削波電路
旨在衰減輸入訊號正部分的削波電路可以稱為正削波器。在正二極體削波電路中,我們有以下型別:
- 正串聯削波器
- 帶正 $V_{r}$(參考電壓)的正串聯削波器
- 帶負 $V_{r}$ 的正串聯削波器
- 正並聯削波器
- 帶正 $V_{r}$ 的正並聯削波器
- 帶負 $V_{r}$ 的正並聯削波器
讓我們詳細討論每種型別。
正串聯削波器
在削波電路中,二極體與輸入訊號串聯連線,並衰減波形的正部分,這稱為正串聯削波器。下圖表示正串聯削波器的電路圖。
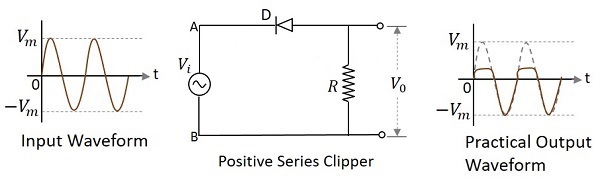
輸入的正半週期 - 當施加輸入電壓時,輸入的正半週期使電路中的 A 點相對於 B 點為正。這使得二極體反向偏置,因此它表現為開路開關。因此,負載電阻上的電壓變為零,因為沒有電流流過它,因此 $V_{0}$ 將為零。
輸入的負半週期 - 輸入的負半週期使電路中的 A 點相對於 B 點為負。這使得二極體正向偏置,因此它像閉合開關一樣導通。因此,負載電阻上的電壓將等於施加的輸入電壓,因為它完全出現在輸出 $V_{0}$ 上。
波形
在上圖中,如果觀察波形,我們可以理解只有正峰值的一部分被削波了。這是由於 $V_{0}$ 上的電壓造成的。但理想輸出並非如此。讓我們看一下下圖。

與理想輸出不同,由於二極體導通電壓為 0.7v,因此實際輸出中存在正半週期的一小部分。因此,實際輸出波形和理想輸出波形之間存在差異。
帶正 $V_{r}$ 的正串聯削波器
在削波電路中,二極體與輸入訊號串聯連線,並用正參考電壓 $V_{r}$ 偏置,並衰減波形的正部分,這稱為帶正 $V_{r}$ 的正串聯削波器。下圖表示當施加的參考電壓為正時,正串聯削波器的電路圖。
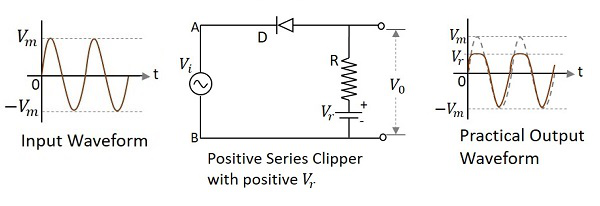
在輸入的正半週期期間,二極體反向偏置,參考電壓出現在輸出端。在其負半週期期間,二極體正向偏置並像閉合開關一樣導通。因此,輸出波形如上圖所示。
帶負 $V_{r}$ 的正串聯削波器
在削波電路中,二極體與輸入訊號串聯連線,並用負參考電壓 $V_{r}$ 偏置,並衰減波形的正部分,這稱為帶負 $V_{r}$ 的正串聯削波器。下圖表示當施加的參考電壓為負時,正串聯削波器的電路圖。

在輸入的正半週期期間,二極體反向偏置,參考電壓出現在輸出端。由於參考電壓為負,因此顯示了具有恆定幅度的相同電壓。在其負半週期期間,二極體正向偏置並像閉合開關一樣導通。因此,大於參考電壓的輸入訊號出現在輸出端。
正並聯削波器
在削波電路中,二極體與輸入訊號並聯連線,並衰減波形的正部分,這稱為正並聯削波器。下圖表示正並聯削波器的電路圖。
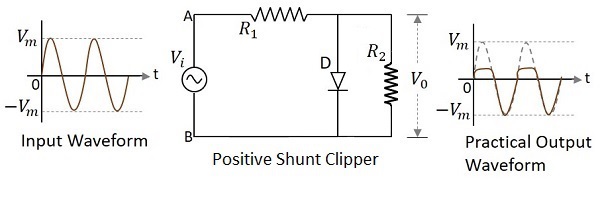
輸入的正半週期 - 當施加輸入電壓時,輸入的正半週期使電路中的 A 點相對於 B 點為正。這使得二極體正向偏置,因此它像閉合開關一樣導通。因此,負載電阻上的電壓變為零,因為沒有電流流過它,因此 $V_{0}$ 將為零。
輸入的負半週期 - 輸入的負半週期使電路中的 A 點相對於 B 點為負。這使得二極體反向偏置,因此它表現為開路開關。因此,負載電阻上的電壓將等於施加的輸入電壓,因為它完全出現在輸出 $V_{0}$ 上。
波形
在上圖中,如果觀察波形,我們可以理解只有正峰值的一部分被削波了。這是由於 $V_{0}$ 上的電壓造成的。但理想輸出並非如此。讓我們看一下下圖。
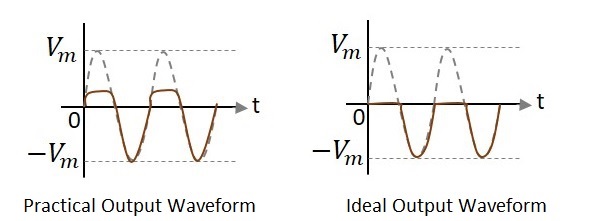
與理想輸出不同,由於二極體導通電壓為 0.7v,因此實際輸出中存在正半週期的一小部分。因此,實際輸出波形和理想輸出波形之間存在差異。
帶正 $V_{r}$ 的正並聯削波器
在削波電路中,二極體與輸入訊號並聯連線,並用正參考電壓 $V_{r}$ 偏置,並衰減波形的正部分,這稱為帶正 $V_{r}$ 的正並聯削波器。下圖表示當施加的參考電壓為正時,正並聯削波器的電路圖。

在輸入的正半週期期間,二極體正向偏置,輸出端只有參考電壓。在其負半週期期間,二極體反向偏置並表現為開路開關。整個輸入都出現在輸出端。因此,輸出波形如上圖所示。
帶負 $V_{r}$ 的正並聯削波器
在削波電路中,二極體與輸入訊號並聯連線,並用負參考電壓 $V_{r}$ 偏置,並衰減波形的正部分,這稱為帶負 $V_{r}$ 的正並聯削波器。
下圖表示當施加的參考電壓為負時,正並聯削波器的電路圖。
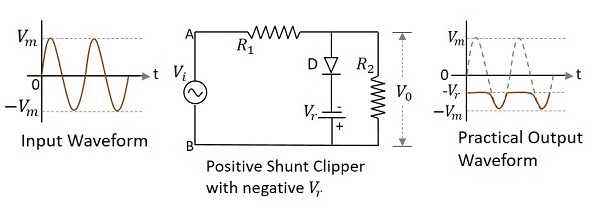
在輸入訊號的正半週期間,二極體正向偏置,參考電壓出現在輸出端。由於參考電壓為負,因此顯示相同幅度的恆定電壓。在其負半週期間,二極體反向偏置並表現為開路開關。因此,大於參考電壓的輸入訊號出現在輸出端。
電子電路 - 負鉗位電路
旨在衰減輸入訊號負部分的鉗位電路可以稱為負鉗位器。在負二極體鉗位電路中,我們有以下型別。
- 負串聯鉗位
- 帶正$V_{r}$(參考電壓)的負串聯鉗位
- 帶負$V_{r}$的負串聯鉗位
- 負並聯鉗位
- 帶正$V_{r}$的負並聯鉗位
- 帶負$V_{r}$的負並聯鉗位
讓我們詳細討論每種型別。
負串聯鉗位
二極體串聯連線到輸入訊號並衰減波形負部分的鉗位電路稱為負串聯鉗位。下圖表示負串聯鉗位電路圖。
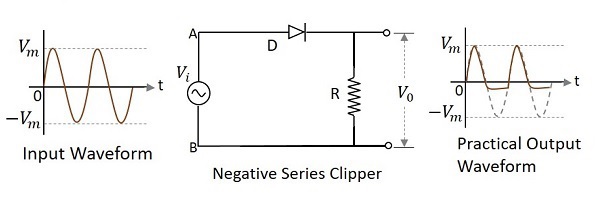
輸入訊號的正半周 - 當施加輸入電壓時,輸入訊號的正半周使電路中A點相對於B點為正。這使得二極體正向偏置,因此它像一個閉合開關。因此,輸入電壓完全出現在負載電阻兩端,以產生輸出$V_{0}$。
輸入訊號的負半周 - 輸入訊號的負半周使電路中A點相對於B點為負。這使得二極體反向偏置,因此它像一個開路開關。因此,負載電阻上的電壓將為零,使$V_{0}$為零。
波形
在上圖中,如果觀察波形,我們可以理解只有負峰的一部分被鉗位了。這是由於$V_{0}$上的電壓造成的。但理想輸出並非如此。讓我們看看下圖。

與理想輸出不同,由於二極體導通電壓為0.7v,實際輸出中存在負半周的一小部分。因此,實際輸出波形和理想輸出波形之間存在差異。
帶正$V_{r}$的負串聯鉗位
二極體串聯連線到輸入訊號並用正參考電壓$V_{r}$偏置並衰減波形負部分的鉗位電路稱為帶正$V_{r}$的負串聯鉗位。下圖表示當施加的參考電壓為正時負串聯鉗位電路圖。

在輸入訊號的正半週期間,只有當陽極電壓值超過二極體的陰極電壓值時,二極體才開始導通。由於陰極電壓等於施加的參考電壓,因此輸出將如所示。
帶負$V_{r}$的負串聯鉗位
二極體串聯連線到輸入訊號並用負參考電壓$V_{r}$偏置並衰減波形負部分的鉗位電路稱為帶負$V_{r}$的負串聯鉗位。下圖表示當施加的參考電壓為負時負串聯鉗位電路圖。
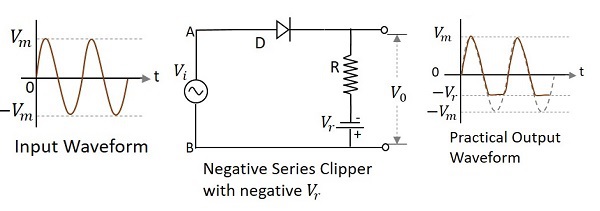
在輸入訊號的正半週期間,二極體正向偏置,輸入訊號出現在輸出端。在其負半週期間,二極體反向偏置,因此不會導通。但是,施加的負參考電壓出現在輸出端。因此,輸出波形的負半周在此參考電平後被鉗位。
負並聯鉗位
二極體並聯連線到輸入訊號並衰減波形負部分的鉗位電路稱為負並聯鉗位。下圖表示負並聯鉗位電路圖。
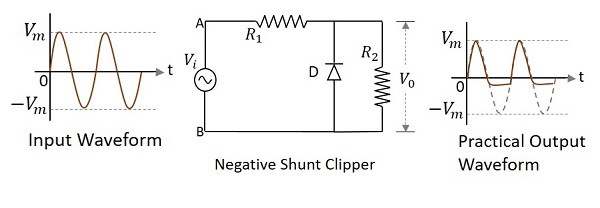
輸入訊號的正半周 - 當施加輸入電壓時,輸入訊號的正半周使電路中A點相對於B點為正。這使得二極體反向偏置,因此它表現為開路開關。因此,負載電阻上的電壓等於施加的輸入電壓,因為它完全出現在輸出$V_{0}$上
輸入訊號的負半周 - 輸入訊號的負半周使電路中A點相對於B點為負。這使得二極體正向偏置,因此它像閉合開關一樣導通。因此,負載電阻上的電壓變為零,因為沒有電流流過它。
波形
在上圖中,如果觀察波形,我們可以理解只有負峰的一部分被鉗位了。這是由於$V_{0}$上的電壓造成的。但理想輸出並非如此。讓我們看看下圖。

與理想輸出不同,由於二極體導通電壓為0.7v,實際輸出中存在負半周的一小部分。因此,實際輸出波形和理想輸出波形之間存在差異。
帶正$V_{r}$的負並聯鉗位
二極體並聯連線到輸入訊號並用正參考電壓$V_{r}$偏置並衰減波形負部分的鉗位電路稱為帶正$V_{r}$的負並聯鉗位。下圖表示當施加的參考電壓為正時負並聯鉗位電路圖。
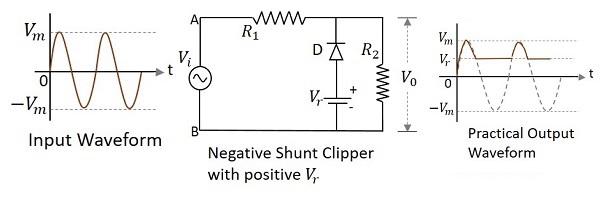
在輸入訊號的正半週期間,二極體反向偏置並表現為開路開關。因此,整個輸入電壓(大於施加的參考電壓)出現在輸出端。低於參考電壓電平的訊號被鉗位。
在負半週期間,由於二極體正向偏置且迴路完成,因此沒有輸出。
帶負$V_{r}$的負並聯鉗位
二極體並聯連線到輸入訊號並用負參考電壓$V_{r}$偏置並衰減波形負部分的鉗位電路稱為帶負$V_{r}$的負並聯鉗位。下圖表示當施加的參考電壓為負時負並聯鉗位電路圖。
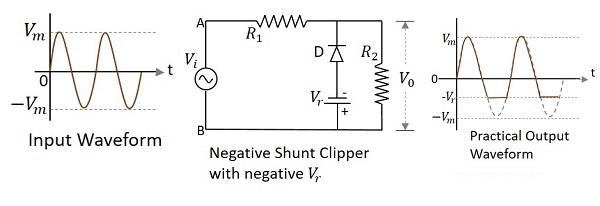
在輸入訊號的正半週期間,二極體反向偏置並表現為開路開關。因此,整個輸入電壓出現在輸出$V_{o}$上。在負半週期間,二極體正向偏置。高達參考電壓的負電壓出現在輸出端,其餘訊號被鉗位。
雙向鉗位
這是一個帶參考電壓$V_{r}$的正負鉗位器。輸入電壓被雙向鉗位,即輸入波形的正負部分都使用兩個參考電壓進行鉗位。為此,兩個二極體$D_{1}$和$D_{2}$以及兩個參考電壓$V_{r1}$和$V_{r2}$連線在電路中。
此電路也稱為組合鉗位電路。下圖顯示了雙向或組合鉗位電路的電路佈置及其輸出波形。

在輸入訊號的正半週期間,二極體$D_{1}$導通,使參考電壓$V_{r1}$出現在輸出端。在輸入訊號的負半週期間,二極體$D_{2}$導通,使參考電壓$V_{r1}$出現在輸出端。因此,兩個二極體交替導通,在兩個週期內鉗位輸出。輸出取自負載電阻兩端。
至此,我們完成了主要的鉗位電路。讓我們在下一章中學習箝位電路。
電子電路 - 箝位電路
箝位電路是一種向交流訊號新增直流電平的電路。實際上,可以使用箝位電路將訊號的正負峰值置於所需的電平。由於直流電平發生偏移,因此箝位電路稱為電平移位器。
箝位電路包含電容等儲能元件。一個簡單的箝位電路包括一個電容、一個二極體、一個電阻以及如果需要的話一個直流電池。
箝位電路
箝位電路可以定義為包含二極體、電阻和電容的電路,該電路將波形移至所需的直流電平,而不會改變施加訊號的實際外觀。
為了保持波形週期,τ必須大於週期的一半(電容的放電時間應緩慢)。
$$\tau = Rc$$
其中
- R是所用電阻的阻值
- C是所用電容的電容值
電容的充放電時間常數決定了箝位電路的輸出。
在箝位電路中,輸出波形相對於輸入訊號發生向上或向下的垂直偏移。
負載電阻和電容會影響波形。因此,電容的放電時間應足夠長。
當使用耦合電容網路(因為電容阻擋直流)時,輸入訊號中存在的直流分量會被抑制。因此,當需要恢復直流時,使用箝位電路。
箝位電路的型別
箝位電路有幾種型別,例如
- 正箝位
- 帶正$V_r$的正箝位
- 帶負$V_r$的正箝位
- 負箝位
- 帶正$V_{r}$的負箝位
- 帶負$V_{r}$的負箝位
讓我們詳細瞭解一下。
正箝位電路
箝位電路恢復直流電平。當訊號的負峰值被抬高到零電平以上時,則稱該訊號被正箝位。
正箝位電路是一種包含二極體、電阻和電容的電路,它將輸出訊號移至輸入訊號的正部分。下圖說明了正箝位電路的構造。

最初,當施加輸入時,電容尚未充電,二極體反向偏置。此時不考慮輸出。在負半週期間,在峰值時,電容被充電,一極板帶負電,另一極板帶正電。電容現在被充電到其峰值$V_{m}$。二極體正向偏置並大量導通。
在下一個正半週期間,電容被充電到正Vm,而二極體反向偏置並開路。此時電路的輸出為
$$V_{0}=V_{i}+V_{m}$$
因此,訊號被正箝位,如上圖所示。輸出訊號根據輸入訊號的變化而變化,但根據電容上的電荷偏移電平,因為它會新增輸入電壓。
帶正Vr的正箝位
如果正箝位電路用某個正參考電壓偏置,則該電壓將被新增到輸出中以提高鉗位電平。利用這一點,帶正參考電壓的正箝位電路構造如下。

在正半週期間,參考電壓透過二極體施加到輸出端,並且隨著輸入電壓的增加,二極體的陰極電壓相對於陽極電壓增加,因此它停止導通。在負半週期間,二極體正向偏置並開始導通。電容兩端的電壓和參考電壓共同維持輸出電壓電平。
帶負$V_{r}$的正箝位
如果正箝位電路用某個負參考電壓偏置,則該電壓將被新增到輸出中以提高鉗位電平。利用這一點,帶正參考電壓的正箝位電路構造如下。

在正半週期間,電容兩端的電壓和參考電壓共同維持輸出電壓電平。在負半週期間,當陰極電壓小於陽極電壓時,二極體導通。這些變化使輸出電壓如上圖所示。
負箝位
負箝位電路是一種包含二極體、電阻和電容的電路,它將輸出訊號移至輸入訊號的負部分。下圖說明了負箝位電路的構造。
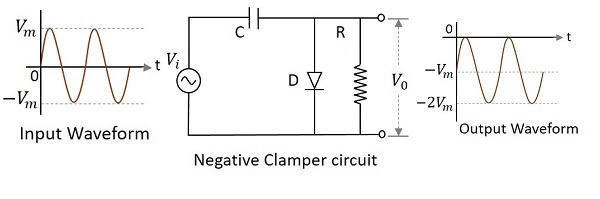
在正半週期間,電容被充電到其峰值 $v_{m}$。二極體處於正向偏置並導通。在負半週期間,二極體處於反向偏置並斷路。此時電路的輸出將是
$$V_{0}=V_{i}+V_{m}$$
因此,訊號被負鉗位,如上圖所示。輸出訊號根據輸入訊號的變化而變化,但根據電容器上的電荷偏移電平,因為它會疊加輸入電壓。
帶正 Vr 的負鉗位電路
如果負鉗位電路偏置某個正參考電壓,則該電壓將新增到輸出以提高鉗位電平。利用這一點,帶正參考電壓的負鉗位電路構建如下。

儘管輸出電壓被負鉗位,但輸出波形的一部分被提升到正電平,因為施加的參考電壓為正。在正半週期間,二極體導通,但輸出等於施加的正參考電壓。在負半週期間,二極體充當斷路,電容器兩端的電壓形成輸出。
帶負 Vr 的負鉗位電路
如果負鉗位電路偏置某個負參考電壓,則該電壓將新增到輸出以提高鉗位電平。利用這一點,帶負參考電壓的負鉗位電路構建如下。
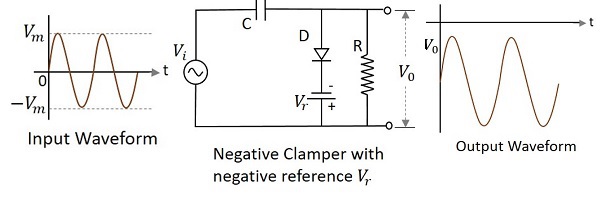
二極體的陰極連線到負參考電壓,該電壓小於零和陽極電壓。因此,二極體在正半週期間開始導通,早於零電壓電平。在負半週期間,電容器兩端的電壓出現在輸出端。因此,波形被鉗位到負部分。
應用
限幅器和鉗位器都有許多應用,例如
限幅器
- 用於波形的產生和整形
- 用於保護電路免受尖峰干擾
- 用作幅度恢復器
- 用作電壓限制器
- 用於電視電路
- 用於調頻發射機
鉗位器
- 用作直流恢復器
- 用於消除失真
- 用作電壓倍增器
- 用於保護放大器
- 用作測試裝置
- 用作基線穩定器
限幅器和電壓倍增器
除了限幅器和鉗位器等波形整形電路外,二極體還用於構建其他電路,例如限幅器和電壓倍增器,我們將在本章中討論這些電路。二極體還有另一個重要的應用,稱為整流器,我們將在後面討論。
限幅器
在瀏覽這些限幅器和鉗位器時,我們經常遇到的另一個名稱是限幅器電路。限幅器電路可以理解為限制輸出電壓不超過預定值的電路。
這或多或少是一個限幅器電路,不允許指定的訊號值超過。實際上,削波可以被認為是限幅的極端程度。因此,限幅可以理解為平滑削波。
下圖顯示了一些限幅器電路的示例:

可以從限幅器電路的傳輸特性曲線瞭解其效能。此類曲線的示例如下。
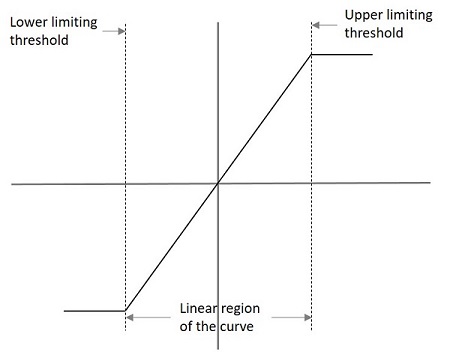
圖中指定了上下限,指示了限幅器特性。此類圖形的輸出電壓可以理解為
$$V_{0}= L_{-},KV_{i},L_{+}$$
其中
$$L_{-}=V_{i}\leq \frac{L_{-}}{k}$$
$$KV_{i}=\frac{L_{-}}{k}< V_{i}<\frac{L_{+}}{k}$$
$$L_{+}=V_{i}\geq \frac{L_{+}}{K}$$
限幅器的型別
限幅器有幾種型別,例如
單極性限幅器 - 此電路單向限制訊號。
雙極性限幅器 - 此電路雙向限制訊號。
軟限幅器 - 在此電路中,即使輸入發生微小變化,輸出也可能發生變化。
硬限幅器 - 輸出不會隨著輸入訊號的變化而輕易改變。
單限幅器 - 此電路使用一個二極體進行限幅。
雙限幅器 - 此電路使用兩個二極體進行限幅。
電壓倍增器
在某些情況下,需要將電壓倍增。這可以透過使用二極體和電容器的簡單電路輕鬆實現。如果電壓加倍,則此類電路稱為電壓倍增器。這可以擴充套件為製作電壓三倍器或電壓四倍器等,以獲得高直流電壓。
為了更好地理解,讓我們考慮一個將電壓乘以 2 的電路。此電路可以稱為電壓倍增器。下圖顯示了電壓倍增器的電路。
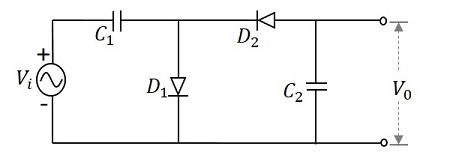
施加的輸入電壓將是交流訊號,形式為正弦波,如下圖所示。
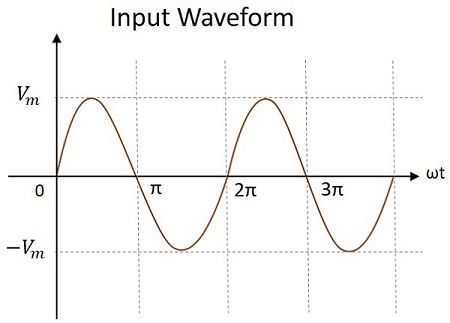
工作原理
可以透過分析輸入訊號的每個半週期來理解電壓倍增器電路。每個週期都會使二極體和電容器以不同的方式工作。讓我們試著理解這一點。
在第一個正半週期間 - 當施加輸入訊號時,電容器 $C_{1}$ 被充電,二極體 $D_{1}$ 處於正向偏置。而二極體 $D_{2}$ 處於反向偏置,電容器 $C_{2}$ 沒有得到任何電荷。這使得輸出 $V_{0}$ 為 $V_{m}$
這可以從下圖理解。
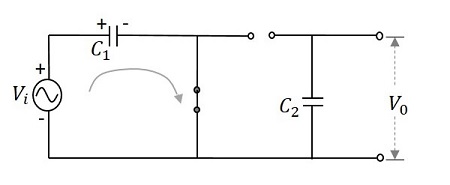
因此,在 0 到 $\pi$ 之間,產生的輸出電壓將為 $V_{max}$。電容器 $C_{1}$ 透過正向偏置的二極體 $D_{1}$ 充電以提供輸出,而 $C_{2}$ 不會充電。此電壓出現在輸出端。
在負半週期間 - 之後,當負半周到來時,二極體 $D_{1}$ 處於反向偏置,二極體 $D_{2}$ 處於正向偏置。二極體 $D_{2}$ 透過電容器 $C_{2}$ 獲得電荷,該電容器在此過程中被充電。然後電流流過電容器 $C_{1}$,該電容器放電。這可以從下圖理解。
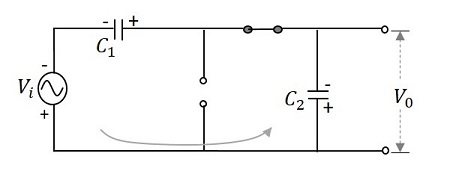
因此,在 $\pi$ 到 $2\pi$ 之間,電容器 $C_{2}$ 兩端的電壓將為 $V_{max}$。而完全充電的電容器 $C_{1}$ 傾向於放電。現在,來自兩個電容器的電壓一起出現在輸出端,即 $2V_{max}$。因此,此週期內的輸出電壓 $V_{0}$ 為 $2V_{max}$
在下一個正半週期間 - 電容器 $C_{1}$ 從電源充電,二極體 $D_{1}$ 處於正向偏置。電容器 $C_{2}$ 保持電荷,因為它找不到放電的方式,二極體 $D_{2}$ 處於反向偏置。現在,此週期的輸出電壓 $V_{0}$ 獲得了來自兩個電容器的電壓,它們一起出現在輸出端,即 $2V_{max}$。
在下一個負半週期間 - 下一個負半周使電容器 $C_{1}$ 再次從其滿電荷放電,二極體 $D_{1}$ 反向偏置,而 $D_{2}$ 正向偏置,電容器 $C_{2}$ 進一步充電以保持其電壓。現在,此週期的輸出電壓 $V_{0}$ 獲得了來自兩個電容器的電壓,它們一起出現在輸出端,即 $2V_{max}$。
因此,輸出電壓 $V_{0}$ 在整個工作過程中保持為 $2V_{max}$,這使得電路成為電壓倍增器。
電壓倍增器主要用於需要高直流電壓的地方。例如,陰極射線管和計算機顯示器。
分壓器
雖然二極體用於倍增電壓,但一組串聯電阻可以構成一個小網路來分壓。此類網路稱為分壓器網路。
分壓器是一種將較大電壓轉換為較小電壓的電路。這是使用串聯連線的電阻器完成的。輸出將是輸入的一部分。輸出電壓取決於它驅動的負載的電阻。
讓我們試著瞭解分壓器電路的工作原理。下圖是一個簡單分壓器網路的示例。
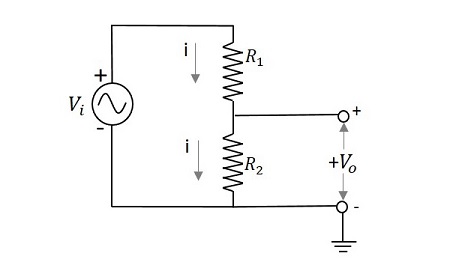
如果我們嘗試為輸出電壓推匯出表示式,則
$$V_{i}=i\left ( R_{1}+R_{2} \right )$$
$$i=\frac{V-{i}}{\left ( R_{1}+R_{2} \right )}$$
$$V_{0}=i \:R_{2}\rightarrow \:i\:=\frac{V_{0}}{R_{2}}$$
比較兩者,
$$\frac{V_{0}}{R_{2}}=\frac{V_{i}}{\left ( R_1 + R_{2} \right )}$$
$$V_{0}=\frac{V_{i}}{\left ( R_1 + R_{2} \right )}R_{2}$$
這是獲得輸出電壓值的表示式。因此,輸出電壓根據網路中電阻器的電阻值進行分配。新增更多電阻器以獲得不同分數的不同輸出電壓。
讓我們舉一個例子來進一步瞭解分壓器。
示例
計算一個網路的輸出電壓,該網路的輸入電壓為 10v,有兩個串聯電阻 2kΩ 和 5kΩ。

輸出電壓 $V_{0}$ 由下式給出
$$V_{0}=\frac{V_{i}}{\left ( R_1 + R_{2} \right )}R_{2}$$
$$=\frac{10}{\left ( 2 + 5 \right )k\Omega }5k\Omega$$
$$=\frac{10}{7}\times 5=\frac{50}{7}$$
$$=7.142v$$
上述問題的輸出電壓 $V_0$ 為 7.14v
電子電路 - 二極體作為開關
二極體是一個兩端 PN 結,可用於各種應用。其中一個應用是電子開關。PN 結在正向偏置時充當短路,在反向偏置時充當斷路。因此,正向和反向偏置狀態的變化使二極體充當開關,正向為開狀態,反向為關狀態。

電子開關優於機械開關
由於以下原因,電子開關優於機械開關:
- 機械開關容易發生金屬氧化,而電子開關則不會。
- 機械開關具有可動觸點。
- 與電子開關相比,它們更容易受到壓力和應力的影響。
- 機械開關的磨損通常會影響其工作。
因此,電子開關比機械開關更有用。
二極體作為開關的工作原理
每當超過指定電壓時,二極體電阻都會增加,使二極體反向偏置,並充當開路開關。每當施加的電壓低於參考電壓時,二極體電阻都會降低,使二極體正向偏置,並充當閉路開關。
下圖說明了二極體充當開關。

開關二極體具有一個 PN 結,其中 P 區摻雜較輕,N 區摻雜較重。上述電路象徵著當正電壓正向偏置二極體時,二極體導通;當負電壓反向偏置二極體時,二極體截止。
振鈴
當正向電流持續流動時,如果突然施加反向電壓,反向電流會在瞬間流動,而不是立即關閉。漏電流越大,損耗就越大。二極體反向偏置時反向電流的流動有時會產生一些振盪,稱為**振鈴**。
這種振鈴現象是一種損耗,因此應該儘量減少。為此,需要了解二極體的開關時間。
二極體開關時間
在改變偏置條件時,二極體會經歷一個**瞬態響應**。系統對任何突然偏離平衡位置的變化的響應稱為瞬態響應。
從正向偏置到反向偏置以及從反向偏置到正向偏置的突然變化會影響電路。響應此類突然變化所需的時間是定義電開關有效性的重要標準。
二極體恢復其穩態所需的時間稱為**恢復時間**。
二極體從反向偏置狀態切換到正向偏置狀態所需的時間間隔稱為**正向恢復時間($t_{fr}$)**。
二極體從正向偏置狀態切換到反向偏置狀態所需的時間間隔稱為**反向恢復時間($t_{fr}$)**。
為了更清楚地理解這一點,讓我們嘗試分析一下對開關PN接面二極體施加電壓後會發生什麼。
載流子濃度
少數載流子濃度隨著遠離結點而呈指數衰減。當施加電壓時,由於正向偏置條件,一側的大多數載流子會移動到另一側。它們成為另一側的少數載流子。這種濃度在結點處會更高。
例如,如果考慮N型,施加正向偏置後進入N型的過量的空穴會新增到N型材料中已經存在的少數載流子中。
讓我們考慮一些符號。
- P型中的多數載流子(空穴)= $P_{po}$
- N型中的多數載流子(電子)= $N_{no}$
- P型中的少數載流子(電子)= $N_{po}$
- N型中的少數載流子(空穴)= $P_{no}$
**正向偏置條件下** - 少數載流子在結點附近較多,遠離結點較少。下圖說明了這一點。

P型中的過量少數載流子電荷 = $P_n-P_{no}$,其中 $p_{no}$ 為(穩態值)
N型中的過量少數載流子電荷 = $N_p-N_{po}$,其中 $N_{po}$ 為(穩態值)
**反向偏置條件下** - 多數載流子不會透過結點導通電流,因此不參與電流條件。開關二極體在反向方向上會短暫表現為短路。
少數載流子將穿過結點並導通電流,這稱為**反向飽和電流**。下圖表示反向偏置條件下的情況。
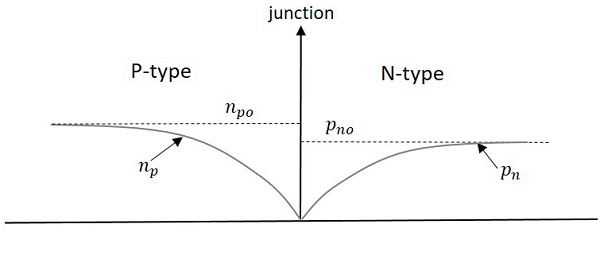
在上圖中,虛線表示平衡值,實線表示實際值。由於少數載流子引起的電流足夠大以導通,因此電路將保持導通狀態,直到去除這種過量電荷。
二極體從正向偏置切換到反向偏置所需的時間稱為**反向恢復時間($t_{rr}$)**。下圖詳細說明了二極體開關時間。
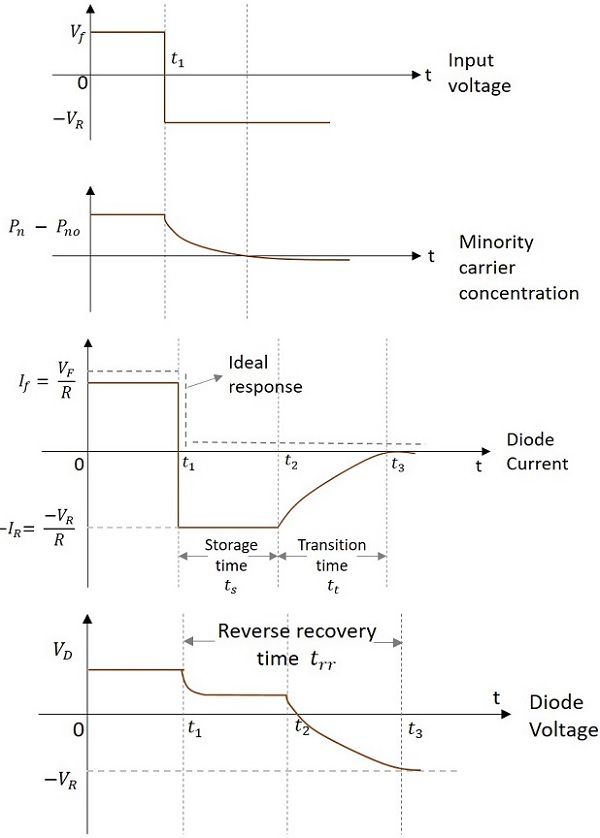
從上圖,讓我們考慮二極體電流圖。
在 $t_{1}$ 時,二極體從導通狀態突然切換到截止狀態;這稱為儲存時間。**儲存時間**是去除過量少數載流子電荷所需的時間。在儲存時間期間,從N型材料流向P型材料的負電流相當大。這個負電流是:
$$-I_R= \frac{-V_{R}}{R}$$
下一個時間段是**過渡時間**”(從 $t_2$ 到 $t_3$)
過渡時間是二極體完全達到開路狀態所需的時間。在 $t_3$ 之後,二極體將處於穩態反向偏置狀態。在 $t_1$ 之前,二極體處於穩態正向偏置狀態。
因此,完全達到開路狀態所需的時間為
$$反向恢復時間\left ( t_{rr} \right )= 儲存時間 \left ( T_{s} \right )+過渡時間 \left ( T_{t} \right )$$
而從截止狀態切換到導通狀態所需的時間較短,稱為**正向恢復時間**。反向恢復時間大於正向恢復時間。如果反向恢復時間縮短,則二極體可以作為更好的開關。
定義
讓我們回顧一下所討論的時間段的定義。
**儲存時間** - 二極體即使在反向偏置狀態下仍保持導通狀態的時間段稱為**儲存時間**。
**過渡時間** - 返回到非導通狀態(即穩態反向偏置)所經過的時間稱為**過渡時間**。
**反向恢復時間** - 二極體從正向偏置切換到反向偏置所需的時間稱為**反向恢復時間**。
**正向恢復時間** - 二極體從反向偏置切換到正向偏置所需的時間稱為**正向恢復時間**。
影響二極體開關時間的因素
有一些因素會影響二極體的開關時間,例如
**二極體電容** - PN接面電容會根據偏置條件而變化。
**二極體電阻** - 二極體改變其狀態所提供的電阻。
**摻雜濃度** - 二極體的摻雜水平會影響二極體的開關時間。
**耗盡層寬度** - 耗盡層寬度越窄,開關速度越快。齊納二極體的耗盡層比雪崩二極體窄,這使得前者成為更好的開關。
應用
二極體開關電路應用廣泛,例如 -
- 高速整流電路
- 高速開關電路
- 射頻接收器
- 通用應用
- 消費類應用
- 汽車應用
- 電信應用等。
電子電路 - 電源
本章開啟了二極體電路另一個部分的新篇章。本章介紹了我們在日常生活中遇到的電源電路。任何電子裝置都包含一個電源單元,該單元為電子裝置的各個部分提供所需的交流或直流電源。
電源的必要性
電子裝置(如計算機、電視機、陰極射線示波器等)包含許多小的部分,但並非所有這些部分都需要我們獲得的230V交流電源。
相反,一個或多個部分可能需要12V直流電源,而其他一些部分可能需要30V直流電源。為了提供所需的直流電壓,必須將輸入的230V交流電源轉換為純直流電源以供使用。**電源單元**正是為此目的而存在的。
一個實際的電源單元如下所示。

現在讓我們瞭解構成電源單元的不同部分。
電源的組成部分
一個典型的電源單元包含以下部分。
**變壓器** - 用於將230V交流電源降壓的輸入變壓器。
**整流器** - 用於將訊號中存在的交流分量轉換為直流分量的整流電路。
**濾波** - 用於平滑整流輸出中存在的波動的濾波電路。
**穩壓器** - 用於將電壓控制到所需輸出水平的穩壓電路。
**負載** - 使用來自穩壓輸出的純直流輸出的負載。
電源單元的框圖
穩壓電源單元的框圖如下所示。
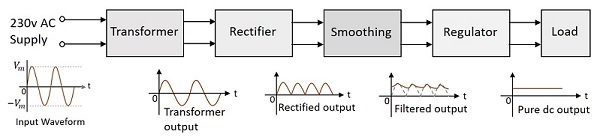
從上圖可以看出,變壓器位於初始階段。雖然我們已經在《基礎電子學》教程中學習了有關變壓器的概念,但讓我們再回顧一下。
變壓器
變壓器有一個**初級線圈**,輸入訊號施加在其上,還有一個**次級線圈**,從中收集輸出訊號。這兩個線圈都繞在一個鐵芯材料上。通常,絕緣體構成變壓器的**鐵芯**。
下圖顯示了一個實際的變壓器。
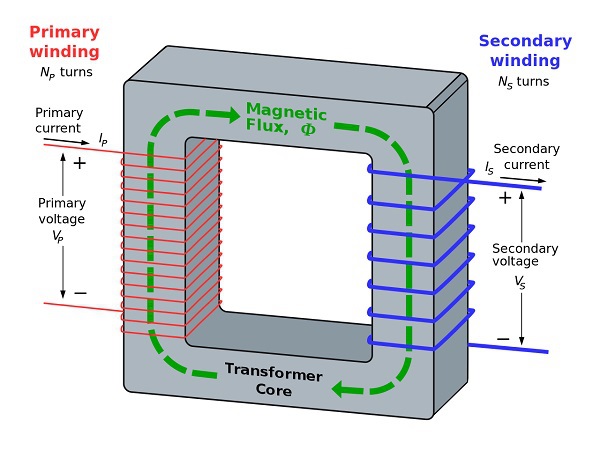
從上圖可以看出,一些符號是通用的。它們如下 -
**$N_{p}$** = 初級繞組的匝數
**$N_{s}$** = 次級繞組的匝數
**$I_{p}$** = 流過變壓器初級的電流
**$I_{s}$** = 流過變壓器次級的電流
**$V_{p}$** = 變壓器初級兩端的電壓
**$V_{s}$** = 變壓器次級兩端的電壓
**$\phi$** = 變壓器鐵芯周圍存在的磁通量
電路中的變壓器
下圖顯示瞭如何在電路中表示變壓器。變壓器的初級繞組、次級繞組和鐵芯也在下圖中表示。
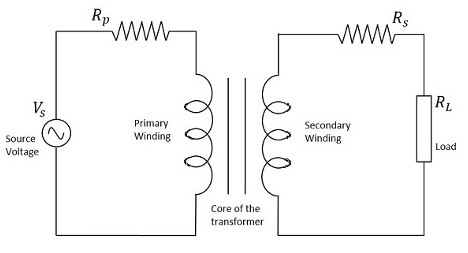
因此,當變壓器連線到電路中時,輸入電源施加到初級線圈,使其產生隨電源變化的磁通量,該磁通量被感應到變壓器的次級線圈中,產生隨磁通量變化的電動勢。由於磁通量必須變化,才能將電動勢從初級傳遞到次級,因此變壓器始終工作在交流電AC上。
根據次級繞組的匝數,變壓器可以分為**升壓**或**降壓**變壓器。
升壓變壓器
當次級繞組的匝數多於初級繞組時,則該變壓器稱為**升壓**變壓器。此處感應電動勢大於輸入訊號。
下圖顯示了升壓變壓器的符號。
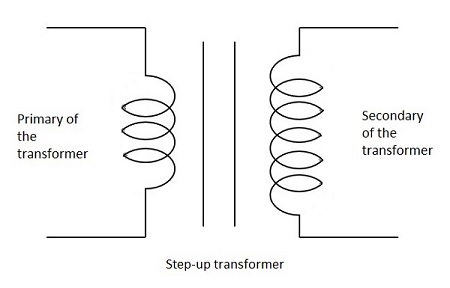
降壓變壓器
當次級繞組的匝數少於初級繞組時,則該變壓器稱為**降壓**變壓器。此處感應電動勢小於輸入訊號。
下圖顯示了降壓變壓器的符號。
在我們的電源電路中,我們使用**降壓變壓器**,因為我們需要將交流電源降低到直流電源。該降壓變壓器的輸出功率會較小,並將作為下一個部分(稱為**整流器**)的輸入。我們將在下一章討論整流器。
電子電路 - 整流器
每當需要將交流電轉換為直流電時,整流電路就會發揮作用。一個簡單的PN接面二極體可以充當整流器。二極體的正向偏置和反向偏置條件實現了整流。
整流
交流電具有持續改變其狀態的特性。透過觀察表示交流電的正弦波可以理解這一點。它在正方向上上升,到達正峰值,然後從那裡下降到正常水平,然後再次進入負方向,達到負峰值,然後再次回到正常水平,並不斷重複。

在波形形成的過程中,我們可以觀察到波形在正負方向上變化。實際上,它完全交替,因此得名交流電。
但在整流過程中,這種交流電會轉換為直流電(DC)。在此之前,在正負方向都流動的波形,在轉換為直流電後,其方向將僅限於正方向。因此,電流僅允許在正方向流動,並在負方向受到阻礙,如下圖所示。
執行整流的電路稱為整流電路。二極體用作整流器,以構建整流電路。
整流電路的型別
整流電路主要有兩種型別,取決於其輸出。它們是
- 半波整流器
- 全波整流器
半波整流器電路僅整流輸入電源的正半週期,而全波整流器電路則整流輸入電源的正負半週期。
半波整流器
半波整流器這個名稱本身就表明整流僅針對週期的一半進行。交流訊號透過輸入變壓器傳遞,根據使用情況進行升壓或降壓。整流電路中大多使用降壓變壓器,以降低輸入電壓。
給變壓器的輸入訊號透過一個充當整流器的PN接面二極體。該二極體僅將輸入的正半週期的交流電壓轉換為脈動直流電壓。負載電阻連線在電路的末端。下圖顯示了半波整流器的電路。
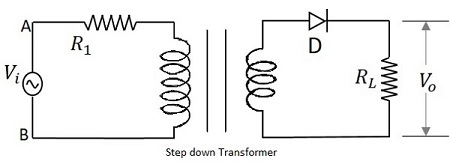
HWR的工作原理
輸入訊號輸入到變壓器,降低電壓水平。變壓器的輸出輸入到充當整流器的二極體。對於輸入訊號的正半週期,該二極體導通(導電)。因此,電流流過電路,並且負載電阻兩端會產生電壓降。二極體在負半週期截止(不導電),因此負半週期的輸出為,$i_{D} = 0$ 和 $V_{o}=0$。
因此,輸出僅存在於輸入電壓的正半週期(忽略反向漏電流)。此輸出將是脈動的,它跨越負載電阻獲取。
HWR的波形
輸入和輸出波形如下圖所示。
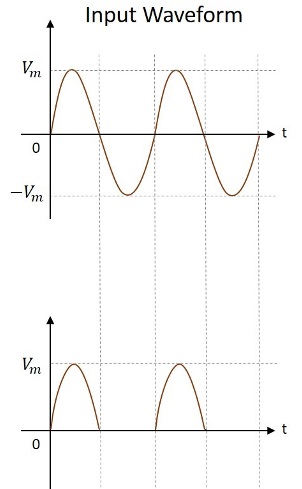
因此,半波整流器的輸出是脈動直流電。讓我們嘗試通過了解從半波整流器輸出獲得的一些值來分析上述電路。
半波整流器的分析
為了分析半波整流器電路,讓我們考慮輸入電壓的方程。
$$v_{i}=V_{m} \sin \omega t$$
$V_{m}$ 是電源電壓的最大值。
假設二極體是理想的。
- 正向電阻,即導通狀態下的電阻為 $R_f$。
- 反向電阻,即截止狀態下的電阻為 $R_r$。
二極體或負載電阻 $R_L$ 中的電流i由下式給出
$i=I_m \sin \omega t \quad for\quad 0\leq \omega t\leq 2 \pi$
$ i=0 \quad\quad\quad\quad for \quad \pi\leq \omega t\leq 2 \pi$
其中
$$I_m= \frac{V_m}{R_f+R_L}$$
直流輸出電流
平均電流 $I_{dc}$ 由下式給出
$$I_{dc}=\frac{1}{2 \pi}\int_{0}^{2 \pi} i \:d\left ( \omega t \right )$$
$$=\frac{1}{2 \pi}\left [ \int_{0}^{\pi}I_m \sin \omega t \:d\left ( \omega t \right )+\int_{0}^{2 \pi}0\: d\left ( \omega t \right )\right ]$$
$$=\frac{1}{2 \pi}\left [ I_m\left \{-\cos \omega t \right \}_{0}^{\pi} \right ]$$
$$=\frac{1}{2 \pi}\left [ I_m\left \{ +1-\left ( -1 \right ) \right \} \right ]=\frac{I_m}{\pi}=0.318 I_m$$
代入 $I_m$ 的值,得到
$$I_{dc}=\frac{V_m}{\pi\left ( R_f+R_L \right )}$$
如果 $R_L >> R_f$,則
$$I_{dc}=\frac{V_m}{\pi R_L}=0.318 \frac{V_m}{R_L}$$
直流輸出電壓
直流輸出電壓由下式給出
$$ V_{dc}=I_{dc}\times R_L=\frac{I_m}{\pi}\times R_L$$
$$=\frac{V_m\times R_L}{\pi\left (R_f+R_L \right )}=\frac{V_m}{\pi\left \{ 1+\left ( R_f/R_L \right ) \right \}}$$
如果 $R_L>>R_f$,則
$$V_{dc}=\frac{V_m}{\pi}=0.318 V_m$$
RMS電流和電壓
RMS電流的值由下式給出
$$I_{rms}=\left [ \frac{1}{2 \pi}\int_{0}^{2\pi} i^{2} d\left ( \omega t \right )\right ]^{\frac{1}{2}}$$
$$I_{rms}=\left [ \frac{1}{2 \pi}\int_{0}^{2\pi}I_{m}^{2} \sin^{2}\omega t \:d\left (\omega t \right ) +\frac{1}{2\pi}\int_{\pi}^{2\pi} 0 \:d\left ( \omega t \right )\right ]^{\frac{1}{2}}$$
$$=\left [ \frac{I_{m}^{2}}{2 \pi}\int_{0}^{\pi}\left ( \frac{1-\cos 2 \omega t}{2} \right )d\left ( \omega t \right ) \right ]^{\frac{1}{2}}$$
$$=\left [ \frac{I_{m}^{2}}{4 \pi}\left \{ \left ( \omega t \right )-\frac{\sin 2 \omega t}{2} \right \}_{0}^{\pi}\right ]^{\frac{1}{2}}$$
$$=\left [ \frac{I_{m}^{2}}{4 \pi}\left \{ \pi - 0 - \frac{\sin 2 \pi}{2}+ \sin 0 \right \} \right ]^{\frac{1}{2}}$$
$$=\left [ \frac{I_{m}^{2}}{4 \pi} \right ]^{\frac{1}{2}}=\frac{I_m}{2}$$
$$=\frac{V_m}{2\left ( R_f+R_L \right )}$$
負載上的RMS電壓為
$$V_{rms}=I_{rms} \times R_L= \frac{V_m \times R_L}{2\left ( R_f+R_L \right )}$$
$$=\frac{V_m}{2\left \{ 1+\left ( R_f/R_L \right ) \right \}}$$
如果 $R_L>>R_f$,則
$$V_{rms}=\frac{V_m}{2}$$
整流效率
任何電路都需要在其工作中保持高效才能獲得更好的輸出。為了計算半波整流器的效率,必須考慮輸出功率與輸入功率之比。
整流效率定義為
$$\eta =\frac{直流功率傳遞到負載}{交流輸入功率來自變壓器副邊}=\frac{P_{ac}}{P_{dc}}$$
現在
$$P_{dc}=\left ( {I_{dc}} \right )^2 \times R_L=\frac{I_m R_L}{\pi^2}$$
此外
$$P_{ac}=P_a+P_r$$
其中
$P_a = 二極體結點處耗散的功率$
$$=I_{rms}^{2}\times R_f=\frac{I_{m}^{2}}{4}\times R_f$$
和
$$P_r = 負載電阻中耗散的功率$$
$$=I_{rms}^{2}\times R_L=\frac{I_{m}^{2}}{4}\times R_L$$
$$P_{ac}=\frac{I_{m}^{2}}{4}\times R_f+\frac{I_{m}^{2}}{4}\times R_L =\frac{I_{m}^{2}}{4}\left ( R_f+R_L \right )$$
從 $P_{ac}$ 和 $P_{dc}$ 的兩個表示式,我們可以寫出
$$\eta =\frac{I_{m}^{2}R_L/\pi^2}{I_{m}^{2}\left ( R_f+R_L \right )/4}=\frac{4}{\pi^2}\frac{R_L}{\left ( R_f+R_L \right )}$$
$$=\frac{4}{\pi^2}\frac{1}{\left \{ 1+\left ( R_f/R_L \right ) \right \}}=\frac{0.406}{\left \{ 1+\left ( R_f/R_L \right ) \right \}}$$
整流效率百分比
$$\eta =\frac{40.6}{\lbrace1+\lgroup\: R_{f}/R_{L}\rgroup\rbrace}$$
理論上,當 $R_{f}/R_{L} = 0$ 時,半波整流器的整流效率最大值為 40.6%。
此外,效率可以透過以下方式計算
$$\eta =\frac{P_{dc}}{P_{ac}}=\frac{\left (I_{dc} \right )^2R_L}{\left ( I_{rms} \right )^2R_L}=\frac{\left ( V_{dc}/R_L \right )^2R_L}{\left (V_{rms}/R_L \right )^2R_L} =\frac{\left ( V_{dc} \right )^2}{\left ( V_{rms} \right )^2}$$
$$=\frac{\left ( V_m/ \pi \right )^2}{\left ( V_m/2 \right )^2}=\frac{4}{\pi^2}=0.406$$
$$=40.6\%$$
紋波係數
整流輸出包含一定量的交流成分,以紋波的形式存在。透過觀察半波整流器的輸出波形可以理解這一點。為了獲得純直流電,我們需要了解此元件。
紋波係數表示整流輸出的波紋度。它用y表示。這可以定義為電壓或電流交流分量的有效值與直流值或平均值之比。
$$\gamma =\frac{紋波電壓}{直流電壓} =\frac{交流分量的rms值}{波形的直流值}=\frac{\left ( V_r \right )_{rms}}{v_{dc}}$$
這裡,
$$\left ( V_r \right )_{rms}=\sqrt{V_{rms}^{2}-V_{dc}^{2}}$$
所以,
$$\gamma =\frac{\sqrt{V_{rms}^{2}-V_{dc}^{2}}}{V_{dc}}=\sqrt{\left (\frac{V_{rms}}{V_{dc}} \right )^2-1}$$
現在,
$$V_{rms}=\left [ \frac{1}{2\pi}\int_{0}^{2\pi} V_{m}^{2} \sin^2\omega t\:d\left ( \omega t \right ) \right ]^{\frac{1}{2}}$$
$$=V_m\left [ \frac{1}{4\pi} \int_{0}^{\pi}\left ( 1- \cos2 \:\omega t \right )d\left ( \omega t \right )\right ]^{\frac{1}{2}}=\frac{V_m}{2}$$
$$V_{dc}=V_{av}=\frac{1}{2\pi}\left [ \int_{0}^{\pi}V_m \sin \omega t \:d\left ( \omega t \right )+\int_{0}^{2\pi} 0.d\left ( \omega t \right )\right ]$$
$$=\frac{V_m}{2 \pi}\left [ -\cos \omega t \right ]_{0}^{\pi}=\frac{V_m}{\pi}$$
$$\gamma =\sqrt{\left [ \left \{ \frac{\left ( V_m/2 \right )}{\left ( V_m/\pi \right )} \right \}^2-1 \right ]}=\sqrt{\left \{ \left ( \frac{\pi}{2} \right )^2-1 \right \}}=1.21$$
紋波係數也定義為
$$\gamma =\frac{\left ( I_r \right )_{rms}}{I_{dc}}$$
由於半波整流器中存在的紋波係數值為 1.21,這意味著輸出中存在的交流量為直流電壓的 121%。
調節
負載電流可能會根據負載電阻而變化。但即使在這種情況下,我們也希望我們跨負載電阻獲取的輸出電壓保持恆定。因此,即使在不同的負載條件下,我們的電壓也需要進行調節。
直流輸出電壓隨直流負載電流變化而變化的特性定義為調節。調節百分比計算如下。
$$調節百分比=\frac{空載電壓-滿載電壓}{滿載電壓} \times 100\%$$
調節百分比越低,電源效能越好。理想電源的調節百分比為零。
變壓器利用率
整流電路中要傳遞到負載的直流功率決定了電路中使用的變壓器的額定值。
因此,變壓器利用率定義為
$$TUF=\frac{要傳遞到負載的直流功率}{變壓器副邊的交流額定值}$$
$$=\frac{P_{d.c}}{P_{a.c\left ( rated \right )}}$$
根據變壓器理論,副邊的額定電壓將為
$$V_m/\sqrt{2}$$
流過它的實際RMS電壓將為
$$I_m/2$$
所以
$$TUF=\frac{\left ( I_m/\pi \right )^2\times R_L}{\left ( V_m/\sqrt{2} \right )\times\left ( I_m/2 \right )}$$
但是
$$V_m=I_m\left ( R_f+R_L \right )$$
所以
$$TUF=\frac{\left ( I_m/\pi \right )^2\times R_L}{\left \{ I_m\left ( R_f+R_L \right )/\sqrt{2} \right \}\times \left ( I_m/2 \right )}$$
$$=\frac{2\sqrt{2}}{\pi^2}\times \frac{R_L}{\left ( R_f+R_L \right )}$$
$$=\frac{2\sqrt{2}}{\pi^2} = 0.287$$
峰值反向電壓
當二極體反向偏置連線時,應在受控的電壓水平下工作。如果超過該安全電壓,二極體會損壞。因此,瞭解該最大電壓非常重要。
二極體在不被破壞的情況下能夠承受的最大反向電壓稱為峰值反向電壓。簡稱PIV。
這裡的PIV就是Vm。
形狀因子
這可以理解為波形上所有點的絕對值的數學平均值。形狀因子定義為RMS值與平均值之比。它用F表示。
$$F=\frac{rms值}{平均值}=\frac{I_m/2}{I_m/\pi}=\frac{0.5I_m}{0.318I_m}=1.57$$
峰值因子
必須考慮紋波中的峰值以瞭解整流的有效性。峰值因子的值也是一個重要的考慮因素。峰值因子定義為峰值與RMS值之比。
所以
$$峰值因子=\frac{峰值}{rms值}=\frac{V_m}{V_m/2}=2$$
所有這些都是研究整流器時需要考慮的重要引數。
電子電路 - 全波整流器
能夠整流正負半週期的整流電路可以稱為全波整流器,因為它整流了整個週期。全波整流器的構造可以分為兩種型別。它們是
- 中心抽頭全波整流器
- 橋式全波整流器
它們各有優缺點。現在讓我們一起了解它們的構造和工作原理以及它們的波形,以瞭解哪一個更好以及原因。
中心抽頭全波整流器
如果一個整流電路的變壓器副繞組設有抽頭,並利用兩個二極體交替工作來整流整個週期,則稱為中心抽頭全波整流電路。與其他情況不同,這裡的變壓器是中心抽頭的。
中心抽頭變壓器的特點如下:
抽頭是在副繞組的中點引出一條引線形成的。這樣做將繞組分成兩個相等的部分。
抽頭中點的電壓為零。這形成了一箇中性點。
中心抽頭提供兩個幅值相等但極性相反的獨立輸出電壓。
可以引出多個抽頭以獲得不同級別的電壓。
中心抽頭變壓器與兩個整流二極體一起用於構建中心抽頭全波整流器。中心抽頭全波整流器的電路圖如下所示。
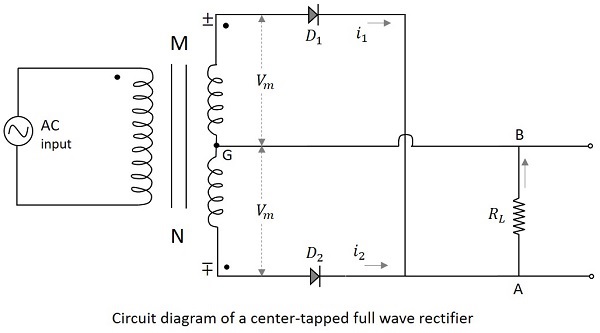
中心抽頭全波整流器(CT-FWR)的工作原理
透過上圖可以理解中心抽頭全波整流器的工作原理。當輸入電壓的正半週期施加時,變壓器副繞組上的點M相對於點N變為正。這使得二極體$D_1$正向偏置。因此,電流$i_1$從A流向B透過負載電阻。現在我們在輸出端得到正半週期。
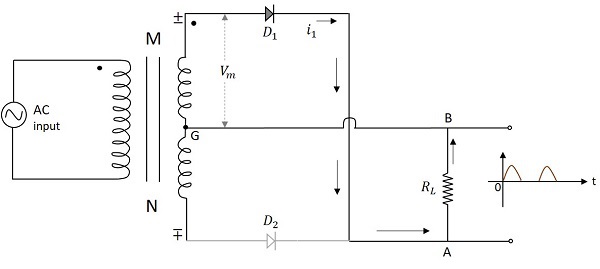
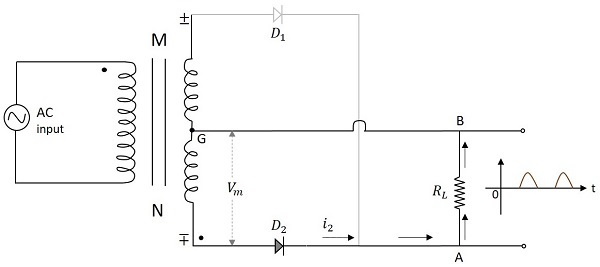
當輸入電壓的負半週期施加時,變壓器副繞組上的點M相對於點N變為負。這使得二極體$D_2$正向偏置。因此,電流$i_2$從A流向B透過負載電阻。現在我們在輸出端得到正半週期,即使在輸入的負半週期期間也是如此。
中心抽頭全波整流器的波形
中心抽頭全波整流器的輸入和輸出波形如下所示。
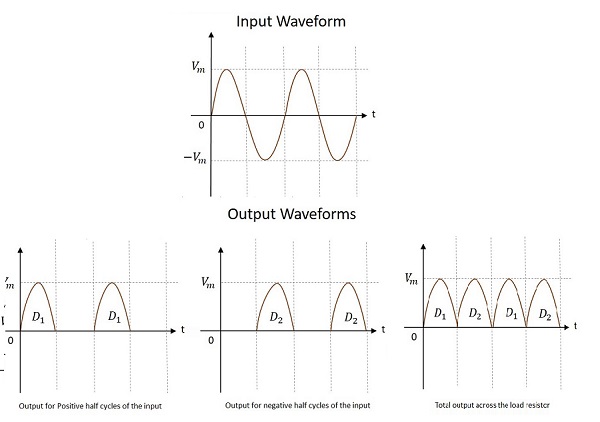
從上圖可以看出,在正負半週期都獲得了輸出。還可以觀察到,負載電阻上的輸出在兩個半週期中方向相同。
峰值反向電壓
由於半個副繞組上的最大電壓為$V_m$,因此整個副繞組電壓出現在不導通的二極體上。因此,反向峰值電壓是半個副繞組最大電壓的兩倍,即
$$PIV=2V_m$$
缺點
中心抽頭全波整流器有一些缺點,例如:
- 中心抽頭的位置難以確定
- 直流輸出電壓小
- 二極體的PIV應較高
下一種全波整流電路是橋式全波整流電路。
橋式全波整流器
這是一種全波整流電路,它利用四個以橋式連線的二極體,不僅可以在輸入的整個週期內產生輸出,還可以消除中心抽頭全波整流電路的缺點。
此電路不需要變壓器的中心抽頭。四個稱為$D_1$、$D_2$、$D_3$和$D_4$的二極體用於構建橋式網路,以便兩個二極體在一個半週期內導通,另外兩個二極體在輸入電源的另一個半週期內導通。橋式全波整流器的電路圖如下所示。
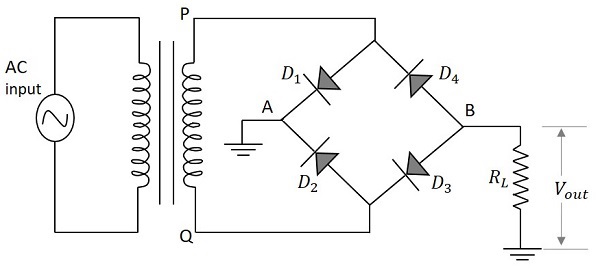
橋式全波整流器的工作原理
採用四個二極體連線在橋式電路中的全波整流器來獲得更好的全波輸出響應。當施加輸入電源的正半週期時,點P相對於點Q變為正。這使得二極體$D_1$和$D_3$正向偏置,而$D_2$和$D_4$反向偏置。這兩個二極體現在將與負載電阻串聯。
下圖顯示了這一點以及電路中的常規電流方向。

因此,二極體$D_1$和$D_3$在輸入電源的正半週期內導通,以在負載電阻上產生輸出。由於兩個二極體協同工作以產生輸出,因此電壓將是中心抽頭全波整流器輸出電壓的兩倍。
當施加輸入電源的負半週期時,點P相對於點Q變為負。這使得二極體$D_1$和$D_3$反向偏置,而$D_2$和$D_4$正向偏置。這兩個二極體現在將與負載電阻串聯。
下圖顯示了這一點以及電路中的常規電流方向。
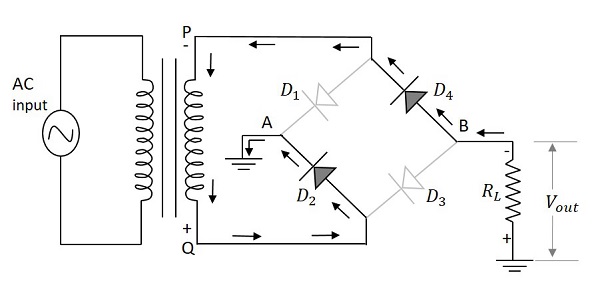
因此,二極體$D_{2}$和$D_{4}$在輸入電源的負半週期內導通,以在負載電阻上產生輸出。這裡也有兩個二極體工作以產生輸出電壓。電流方向與輸入正半週期時相同。
橋式全波整流器的波形
中心抽頭全波整流器的輸入和輸出波形如下所示。
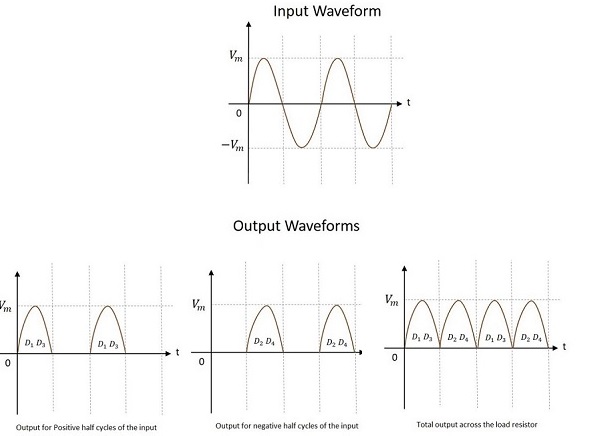
從上圖可以看出,在正負半週期都獲得了輸出。還可以觀察到,負載電阻上的輸出在兩個半週期中方向相同。
峰值反向電壓
當兩個二極體與變壓器的副繞組並聯時,變壓器上的最大副繞組電壓出現在不導通的二極體上,從而形成了整流電路的PIV。因此,反向峰值電壓是副繞組上的最大電壓,即
$$PIV=V_m$$
優點
橋式全波整流器有很多優點,例如:
- 不需要中心抽頭。
- 直流輸出電壓是中心抽頭全波整流器輸出電壓的兩倍。
- 二極體的PIV是中心抽頭全波整流器的一半。
- 電路設計更容易,輸出效果更好。
現在讓我們分析一下全波整流器的特性。
全波整流器的分析
為了分析全波整流電路,讓我們假設輸入電壓$V_{i}$為:
$$V_{i}=V_m \sin \omega t$$
流過負載電阻$R_L$的電流$i_1$由下式給出
$$i_1=I_m \sin \omega t \quad for \quad0 \leq \omega t \leq \pi$$
$$i_1=\quad0 \quad\quad\quad for \quad \pi \leq \omega t \leq 2\pi$$
其中
$$I_m=\frac{V_m}{R_f+R_L}$$
$R_f$為二極體導通時的電阻。
類似地,流過二極體$D_2$和負載電阻RL的電流$i_2$由下式給出:
$$i_2=\quad\:0 \quad\quad\quad for \quad 0 \leq \omega t \leq \pi$$
$$i_2=I_m \sin \omega t \quad for \quad\pi \leq \omega t \leq 2\pi$$
流過$R_L$的總電流是兩個電流$i_1$和$i_2$的和,即
$$i=i_1+i_2$$
直流或平均電流
直流電流表指示的輸出電流的平均值由下式給出
$$I_{dc}=\frac{1}{2\pi} \int_{0}^{2\pi} i_1 \:d\left ( \omega t \right )+\frac{1}{2\pi}\int_{0}^{2\pi}i_2 \:d\left ( \omega t \right )$$
$$=\frac{1}{2\pi\int_{0}^{\pi}}I_m \sin \omega t \:d\left ( \omega t \right )+0+0+$$
$$\frac{1}{2\pi} \int_{0}^{2\pi}I_m \sin \omega t\:d\left ( \omega t \right ) $$
$$=\frac{I_m}{\pi}+ \frac{I_m}{\pi} =\frac{2I_m}{\pi}=0.636I_m$$
這是半波整流器值的二倍。
直流輸出電壓
負載上的直流輸出電壓由下式給出
$$V_{dc}=I_{dc}\times R_L = \frac{2I_mR_L}{\pi}=0.636I_mR_L$$
因此,直流輸出電壓是半波整流器的兩倍。
RMS電流
電流的RMS值由下式給出
$$I_{rms}=\left [ \frac{1}{\pi}\int_{0}^{\pi} t^2 \:d\left ( \omega t \right )\right ]^{\frac{1}{2}}$$
由於電流在兩個半週期中形式相同
$$=\left [ \frac{I_{m}^{2}}{\pi} \int_{0}^{\pi }\sin^2 \omega t\:d\left ( \omega t \right )\right ]^{\frac{1}{2}}$$
$$=\frac{I_m}{\sqrt{2}}$$
整流效率
整流效率定義為
$$\eta=\frac{P_{dc}}{P_{ac}}$$
現在,
$$P_{dc}=\left (V_{dc} \right )^2/R_L=\left ( 2V_m/\pi \right )^2$$
並且,
$$P_{ac}=\left (V_{rms} \right )^2/R_L=\left (V_m/\sqrt{2} \right )^2$$
所以,
$$\eta =\frac{P_{dc}}{P_{ac}}=\frac{\left (2V_m/\pi \right )^2}{\left ( V_m/\sqrt{2} \right )^2}=\frac{8}{\pi^2}$$
$$=0.812=81.2\%$$
整流器的效率可以計算如下:
直流輸出功率,
$$P_{dc}=I_{dc}^{2}R_L=\frac{4I_{m}^{2}}{\pi^2}\times R_L$$
交流輸入功率,
$$P_{ac}=I_{rms}^{2}\left (R_f+R_L \right )=\frac{I_{m}^{2}}{2}\left ( R_f+R_L \right )$$
所以,
$$\eta=\frac{4I_{m}^{2}R_L/\pi^2}{I_{m}^{2}\left ( R_f+R_L \right )/2}=\frac{8}{\pi^2}\frac{R_L}{\left ( R_f+R_L \right )}$$
$$=\frac{0.812}{\left \{ 1+\left ( R_f/R_L \right ) \right \}}$$
因此,百分比效率為
$$=\frac{0.812}{ 1+\left ( R_f+R_L \right )}$$
$$=81.2\% \quad if\: R_f=0$$
因此,全波整流器的效率是半波整流器的兩倍。
紋波係數
全波整流器整流輸出電壓的波形因數由下式給出
$$F=\frac{I_{rms}}{I_{dc}}=\frac{I_m/\sqrt{2}}{2I_m/\pi}=1.11$$
紋波係數$\gamma$定義為(使用交流電路理論)
$$\gamma =\left [ \left ( \frac{I_{rms}}{I_{dc}} \right )-1 \right ]^{\frac{1}{2}}=\left ( F^2 -1\right )^{\frac{1}{2}}$$
$$=\left [ \left ( 1.11 \right )^2 -1\right ]^\frac{1}{2}=0.48$$
這比半波整流器的紋波係數1.21有了很大的改進。
調節
直流輸出電壓由下式給出
$$V_{dc}=\frac{2I_mR_L}{\pi}=\frac{2V_mR_L}{\pi\left ( R_f+R_L \right )}$$
$$=\frac{2V_m}{\pi}\left [ 1-\frac{R_f}{R_f+R_L} \right ]=\frac{2V_m}{\pi}-I_{dc}R_f$$
變壓器利用率
半波整流器的利用率為0.287
中心抽頭整流器有兩個副繞組,因此中心抽頭全波整流器的利用率為
$$\left ( TUF \right )_{avg}=\frac{P_{dc}}{V-A\:rating\:of\:a\:transformer}$$
$$=\frac{\left ( TUF \right )_p+\left ( TUF \right )_s+\left ( TUF \right )_s}{3}$$
$$=\frac{0.812+0.287+0.287}{3}=0.693$$
半波整流器與全波整流器的比較
在瞭解了全波整流器各種引數的所有值之後,讓我們嘗試比較和對比半波整流器和全波整流器的特性。
| 術語 | 半波整流器 | 中心抽頭全波整流器 | 橋式全波整流器 |
|---|---|---|---|
| 二極體數量 | $1$ | $2$ | $4$ |
| 變壓器抽頭 | $否$ | $是$ | $否$ |
| 峰值反向電壓 | $是$ | $V_m$ | $是$ |
| $2V_m$ | $40.6\%$ | $81.2\%$ | $81.2\%$ |
| 最大效率 | 40.6% | 81.2% | 81.2% |
| 81.2% | 平均/直流電流 | $I_m/\pi$ | $I_m/\pi$ |
| $2I_m/\pi$ | $2I_m/\pi$ | 直流電壓 | 直流電壓 |
| 紋波係數 | $1.21$ | $0.48$ | $0.48$ |
| $V_m/\pi$ | $2V_m/\pi$ | $2V_m/\pi$ | $2V_m/\pi$ |
電子電路 - 濾波器
RMS電流
$I_m/2$
$I_m/\sqrt{2}$
$I_m/\sqrt{2}$
輸出頻率
$f_{in}$

$2f_{in}$
電感器允許直流電透過並阻隔交流電。
電容器允許交流電透過並阻隔直流電。
讓我們嘗試使用這兩個元件構建一些濾波器。
串聯電感濾波器
由於電感器允許直流電透過並阻隔交流電,因此可以透過將電感器串聯連線在整流器和負載之間來構建一個稱為串聯電感濾波器的濾波器。下圖顯示了串聯電感濾波器的電路圖。
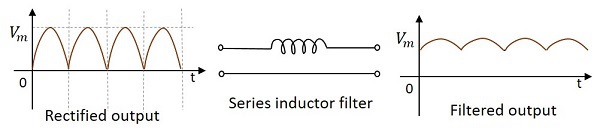
當經過此濾波器時,整流輸出中的交流分量會被電感器阻隔,從而提供純直流電。這是一個簡單的初級濾波器。
並聯電容濾波器
由於電容器允許交流電透過並阻隔直流電,因此可以使用一個並聯連線的電容器來構建一個稱為並聯電容濾波器的濾波器,如下圖所示。
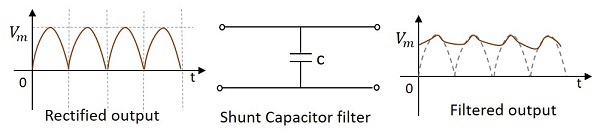
當經過此濾波器時,訊號中的交流分量透過允許交流分量的電容器接地。訊號中剩餘的直流分量則被收集到輸出端。
以上討論的濾波器型別都是使用電感器或電容器構建的。現在,讓我們嘗試同時使用它們來構建一個更好的濾波器。這些是組合濾波器。
LC濾波器
可以使用電感器和電容器來構建濾波器電路,以獲得更好的輸出,其中可以利用電感器和電容器的效率。下圖顯示了LC濾波器的電路圖。

當整流輸出訊號輸入到該電路時,電感器允許直流分量透過,並阻隔訊號中的交流分量。現在,如果訊號中還有任何剩餘的交流分量,它們會被接地,以便我們獲得純直流輸出。
此濾波器也稱為扼流輸入濾波器,因為輸入訊號首先進入電感器。此濾波器的輸出比之前的濾波器更好。
π型濾波器(Pi濾波器)
這是另一種非常常用的濾波器電路型別。它在輸入端有一個電容器,因此也稱為電容輸入濾波器。這裡,兩個電容器和一個電感器以π形網路連線。一個並聯電容器,然後是一個串聯電感器,再然後是另一個並聯電容器構成了此電路。
如果需要,可以根據要求新增幾個相同的節段。下圖顯示了一個π型濾波器(Pi濾波器)的電路圖。

π型濾波器的工作原理
在此電路中,我們有一個並聯電容器,然後是一個串聯電感器,再然後是另一個並聯電容器。
電容器C1 - 此濾波電容器對直流電具有高電抗,對交流電具有低電抗。在將訊號中的交流分量接地後,訊號傳遞到電感器進行進一步濾波。
電感器L - 此電感器對直流分量具有低電抗,同時阻隔任何可能透過電容器C1的交流分量。
電容器C2 - 現在,使用此電容器進一步平滑訊號,以便允許訊號中存在的任何交流分量,這些分量是電感器未能阻隔的。
因此,我們在負載端獲得了所需的純直流輸出。
電子電路 - 穩壓器
電源系統中負載之前的下一個也是最後一個階段是穩壓器部分。現在讓我們嘗試瞭解什麼是穩壓器以及它做什麼。
處理電力控制和轉換的電子學部分可以稱為電力電子學。穩壓器是電力電子學中一個重要的器件,因為它控制著電力輸出。
穩壓器的必要性
為了使電源產生恆定的輸出電壓,而不管輸入電壓變化或負載電流變化如何,都需要一個電壓穩壓器。
電壓穩壓器是一種能夠維持恆定輸出電壓的器件,即使輸入電壓發生波動或負載電流發生變化也不會影響輸出電壓。下圖展示了一個實際穩壓器的外觀。

穩壓器的型別
穩壓器可以根據其工作方式和連線型別分為不同的類別。
根據調節型別,穩壓器主要分為兩種型別:線路穩壓器和負載穩壓器。
線路穩壓器 - 即使輸入線路發生變化,也能使輸出電壓保持恆定的穩壓器稱為線路穩壓器。
負載穩壓器 - 即使輸出端的負載發生變化,也能使輸出電壓保持恆定的穩壓器稱為負載穩壓器。
根據連線型別,電壓穩壓器有兩種型別,它們是
- 串聯電壓穩壓器
- 並聯電壓穩壓器
它們在電路中的佈置方式如下面的圖形所示。
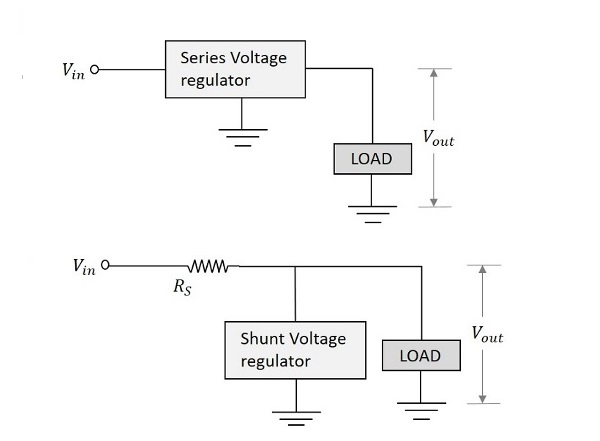
讓我們看看其他重要的穩壓器型別。
穩壓二極體穩壓器
穩壓二極體穩壓器是一種使用穩壓二極體來調節輸出電壓的穩壓器。我們已經在基本電子學教程中討論了有關穩壓二極體的詳細資訊。
當穩壓二極體工作在擊穿或穩壓區時,其兩端的電壓對於電流的大幅變化基本上是恆定的。這種特性使穩壓二極體成為良好的電壓穩壓器。
下圖顯示了一個簡單的穩壓二極體穩壓器的示意圖。

當施加的輸入電壓$V_i$超過穩壓電壓$V_z$時,穩壓二極體開始工作在擊穿區域,並保持負載兩端的電壓恆定。串聯限流電阻$R_s$限制輸入電流。
穩壓二極體穩壓器的工作原理
穩壓二極體能夠保持其兩端的電壓恆定,即使負載變化和輸入電壓波動也如此。因此,我們可以考慮四種情況來理解穩壓二極體穩壓器的工作原理。
情況1 - 如果負載電流$I_L$增加,則穩壓二極體中的電流$I_Z$減小,以保持串聯電阻$R_S$中的電流恆定。輸出電壓Vo取決於輸入電壓Vi和串聯電阻$R_S$兩端的電壓。
這可以寫成
$$V_o=V_{in}-IR_{s}$$
其中$I$是恆定的。因此,$V_o$也保持恆定。
情況2 - 如果負載電流$I_L$減小,則穩壓二極體中的電流$I_Z$增加,因為RS串聯電阻中的電流$I_S$保持恆定。儘管穩壓二極體中的電流$I_Z$增加,但它保持恆定的輸出電壓$V_Z$,從而使負載電壓保持恆定。
情況3 - 如果輸入電壓$V_i$增加,則串聯電阻RS中的電流$I_S$增加。這會增加電阻兩端的電壓降,即$V_S$增加。儘管穩壓二極體中的電流$I_Z$隨著此增加而增加,但穩壓二極體兩端的電壓$V_Z$保持恆定,從而使輸出負載電壓保持恆定。
情況4 - 如果輸入電壓降低,則串聯電阻中的電流降低,這使得穩壓二極體中的電流$I_Z$降低。但由於穩壓二極體的特性,它保持輸出電壓恆定。
穩壓二極體穩壓器的侷限性
穩壓二極體穩壓器有一些侷限性。它們是 -
- 對於大負載電流,效率較低。
- 穩壓二極體的阻抗會稍微影響輸出電壓。
因此,穩壓二極體穩壓器被認為適用於低電壓應用。現在,讓我們瞭解其他使用晶體管制造的電壓穩壓器型別。
電晶體串聯電壓穩壓器
此穩壓器有一個電晶體串聯連線到穩壓二極體穩壓器,兩者並聯連線到負載。電晶體充當可變電阻,調節其集電極發射極電壓以保持輸出電壓恆定。下圖顯示了電晶體串聯電壓穩壓器。

在輸入工作條件下,電晶體基極的電流發生變化。這會影響電晶體基極發射極結電壓$V_{BE}$。輸出電壓由穩壓電壓$V_Z$維持,該電壓是恆定的。由於兩者保持相等,因此輸入電源的任何變化都會透過發射極基極電壓$V_{BE}$的變化來體現。
因此,輸出電壓Vo可以理解為
$$V_O=V_Z+V_{BE}$$
電晶體串聯電壓穩壓器的工作原理
應針對輸入和負載變化考慮串聯電壓穩壓器的工作原理。如果輸入電壓增加,輸出電壓也會增加。但這反過來會導致集電極基極結電壓$V_{BE}$降低,因為穩壓電壓$V_Z$保持恆定。由於發射極集電極區域的電阻增加,因此導通降低。這進一步增加了集電極發射極結電壓VCE,從而降低了輸出電壓$V_O$。當輸入電壓降低時,情況類似。
當負載發生變化時,這意味著如果負載電阻降低,負載電流$I_L$增加,則輸出電壓$V_O$降低,發射極基極電壓$V_{BE}$增加。
隨著發射極基極電壓$V_{BE}$的增加,導通增加,從而降低了發射極集電極電阻。這反過來增加了輸入電流,從而補償了負載電阻的降低。當負載電流增加時,情況類似。
電晶體串聯電壓穩壓器的侷限性
電晶體串聯電壓穩壓器具有以下侷限性 -
- 電壓$V_{BE}$和$V_Z$受溫度升高的影響。
- 無法很好地調節大電流。
- 功耗高。
- 功耗高。
- 效率低。
為了最大限度地減少這些侷限性,可以使用電晶體並聯穩壓器。
電晶體並聯電壓穩壓器
電晶體並聯穩壓器電路是透過將一個電阻串聯連線到輸入端,以及一個電晶體(其基極和集電極透過一個穩壓二極體連線,該穩壓二極體與負載並聯)來形成的。下圖顯示了電晶體並聯穩壓器的電路圖。

電晶體並聯電壓穩壓器的工作原理
如果輸入電壓增加,則$V_{BE}$和$V_O$也會增加。但這只是最初的情況。實際上,當$V_{in}$增加時,電流$I_{in}$也會增加。當此電流流過RS時,會在串聯電阻上產生電壓降$V_S$,該電壓降也會隨著$V_{in}$的增加而增加。但這會導致$V_o$降低。現在,$V_o$的這種降低補償了最初的增加,使其保持恆定。因此,$V_o$保持恆定。如果輸出電壓反而降低,則會發生相反的情況。
如果負載電阻降低,則輸出電壓$V_o$應該降低。流過負載的電流增加。這使得電晶體的基極電流和集電極電流減小。由於電流大量流過,因此串聯電阻兩端的電壓變低。輸入電流將保持恆定。
出現的輸出電壓將是施加電壓$V_i$和串聯電壓降$V_s$之間的差值。因此,輸出電壓將增加以補償最初的下降,並因此保持恆定。如果負載電阻增加,則會發生相反的情況。
積體電路穩壓器
如今,電壓穩壓器以積體電路(IC)的形式出現。這些簡稱為IC穩壓器。
除了像普通穩壓器一樣的功能外,IC穩壓器還具有諸如熱補償、短路保護和浪湧保護等特性,這些特性內置於器件中。
IC穩壓器的型別
IC穩壓器可以是以下型別 -
- 固定正電壓穩壓器
- 固定負電壓穩壓器
- 可調電壓穩壓器
- 雙軌電壓穩壓器
現在讓我們詳細討論它們。
固定正電壓穩壓器
這些穩壓器的輸出固定為特定值,並且這些值是正值,這意味著提供的輸出電壓是正電壓。
最常用的系列是 7800 系列,其積體電路如 IC 7806、IC 7812 和 IC 7815 等,分別提供 +6V、+12V 和 +15V 的輸出電壓。下圖顯示了連線 IC 7810 以提供固定 10V 正穩壓輸出電壓。
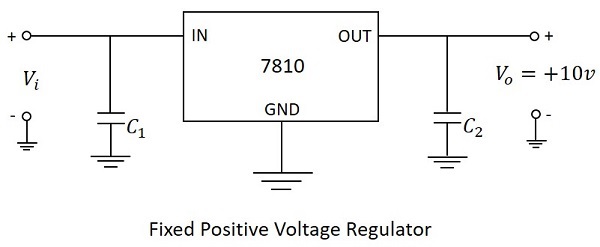
在上圖中,輸入電容 $C_1$ 用於防止不希望的振盪,輸出電容 $C_2$ 充當線路濾波器,以改善瞬態響應。
固定負電壓穩壓器
這些穩壓器的輸出固定為特定值,並且這些值是負的,這意味著提供的輸出電壓為負電壓。
最常用的系列是 7900 系列,其積體電路如 IC 7906、IC 7912 和 IC 7915 等,分別提供 -6V、-12V 和 -15V 的輸出電壓。下圖顯示了連線 IC 7910 以提供固定 10V 負穩壓輸出電壓。
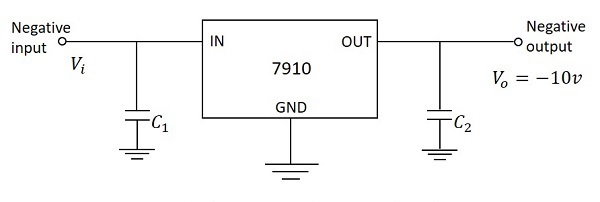
在上圖中,輸入電容 $C_1$ 用於防止不希望的振盪,輸出電容 $C_2$ 充當線路濾波器,以改善瞬態響應。
可調電壓穩壓器
可調電壓穩壓器具有三個端子:IN、OUT 和 ADJ。輸入和輸出端子是共用的,而可調端子配備了一個可變電阻器,使輸出可以在一個較寬的範圍內變化。

上圖顯示了一個非穩壓電源驅動一個常用的 LM 317 可調積體電路穩壓器。LM 317 是一款三端正可調電壓穩壓器,可以在 1.25V 到 37V 的可調輸出範圍內提供 1.5A 的負載電流。
雙軌電壓穩壓器
當需要分壓電源時,使用雙軌穩壓器。它們提供相等正負輸出電壓。例如,RC4195 積體電路提供 +15V 和 -15V 的直流輸出。這需要兩個非穩壓輸入電壓,例如正輸入可能在 +18V 到 +30V 之間變化,負輸入可能在 -18V 到 -30V 之間變化。
上圖顯示了一個雙軌 RC4195 積體電路穩壓器。也可提供輸出在兩個額定限值之間變化的可調雙軌穩壓器。
電子電路 - 開關電源
到目前為止討論的主題代表了電源單元的不同部分。所有這些部分共同構成了**線性電源**。這是從輸入交流電源獲得直流輸出的傳統方法。
線性電源
線性電源 (LPS) 是一種穩壓電源,它在串聯電阻器中耗散大量熱量以調節輸出電壓,輸出電壓具有低紋波和低噪聲。這種 LPS 有許多應用。
線性電源需要更大的半導體器件來調節輸出電壓,併產生更多的熱量,導致能量效率降低。線性電源的瞬態響應時間比其他電源快 100 倍,這在某些專業領域非常重要。
LPS 的優點
- 電源是連續的。
- 電路簡單。
- 這些是可靠的系統。
- 該系統動態響應負載變化。
- 電路電阻發生變化以調節輸出電壓。
- 由於元件工作線上性區域,因此噪聲低。
- 輸出電壓的紋波非常低。
LPS 的缺點
- 使用的變壓器更重且體積更大。
- 散熱更多。
- 線性電源的效率為 40% 到 50%。
- 功率在 LPS 電路中以熱量的形式浪費。
- 獲得單一輸出電壓。
我們已經瞭解了線性電源的不同部分。線性電源的框圖如下所示。

儘管存在上述缺點,但線性電源仍廣泛用於低噪聲放大器、測試裝置、控制電路中。此外,它們還用於資料採集和訊號處理。
所有需要簡單調節且效率不是問題的電源系統都使用 LPS 電路。由於電噪聲較低,因此 LPS 用於為敏感的類比電路供電。但是,為了克服線性電源系統的缺點,使用了開關電源 (SMPS)。
開關電源 (SMPS)
透過實施**開關電源**,克服了 LPS 的缺點,例如效率低、需要大容量電容器來降低紋波以及變壓器笨重且成本高等。
SMPS 的工作原理很簡單,只需瞭解 LPS 中使用的電晶體用於控制壓降,而 SMPS 中的電晶體用作**受控開關**。
工作原理
可以透過下圖瞭解 SMPS 的工作原理。
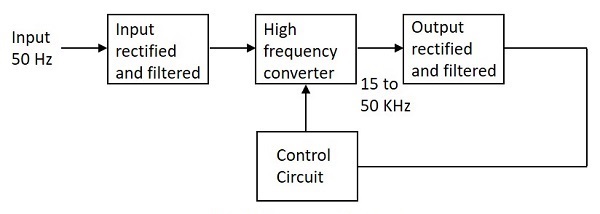
讓我們嘗試瞭解 SMPS 電路的每個階段發生了什麼。
輸入級
將 50Hz 的交流輸入電源訊號直接提供給整流器和濾波器電路組合,無需使用任何變壓器。此輸出將具有許多變化,電容值應更高以處理輸入波動。此非穩壓直流電提供給 SMPS 的中央開關部分。
開關部分
此部分採用快速開關器件(例如功率電晶體或 MOSFET),根據變化情況進行通斷切換,並將此輸出提供給此部分中存在的變壓器的初級繞組。此處使用的變壓器比用於 60Hz 供電的變壓器小得多且輕得多。它們效率更高,因此功率轉換率更高。
輸出級
來自開關部分的輸出訊號再次進行整流和濾波,以獲得所需的直流電壓。這是一個穩壓輸出電壓,然後將其提供給控制電路,該控制電路是一個反饋電路。在考慮反饋訊號後獲得最終輸出。
控制單元
此單元是反饋電路,它包含許多部分。讓我們從下圖中清楚地瞭解這一點。
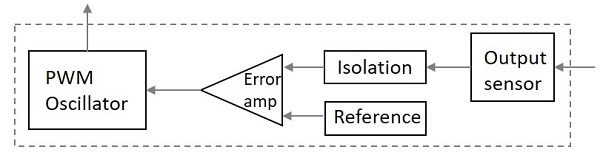
上圖解釋了控制單元的內部部件。輸出感測器感測訊號並將其連線到控制單元。該訊號與其他部分隔離,以便任何突然的尖峰都不會影響電路。參考電壓作為輸入之一以及訊號一起提供給誤差放大器,誤差放大器是一個比較器,它將訊號與所需的訊號電平進行比較。
透過控制斬波頻率來維持最終電壓電平。這是透過比較提供給誤差放大器的輸入來控制的,其輸出有助於確定是否增加或減少斬波頻率。PWM 振盪器產生一個標準的 PWM 波固定頻率。
透過檢視下圖,我們可以更好地瞭解 SMPS 的完整功能。

SMPS 主要用於電壓切換根本不成問題且系統效率確實至關重要的場合。關於 SMPS,需要注意幾點。它們是
SMPS 電路由開關操作,因此電壓持續變化。
開關器件工作在飽和或截止模式。
輸出電壓由反饋電路的開關時間控制。
透過調整佔空比來調整開關時間。
SMPS 的效率很高,因為與其將多餘的功率作為熱量耗散,它會不斷切換其輸入以控制輸出。
缺點
SMPS 存在一些缺點,例如
- 由於高頻切換,存在噪聲。
- 電路複雜。
- 它會產生電磁干擾。
優點
SMPS 的優點包括:
- 效率高達 80% 到 90%。
- 發熱量少;功率損耗少。
- 減少了對電源線的諧波反饋。
- 該裝置結構緊湊,體積小巧。
- 降低了製造成本。
- 提供所需數量電壓的規定。
應用
SMPS 有許多應用。它們用於計算機的主機板、手機充電器、HVDC 測量、電池充電器、中央配電、汽車、消費電子產品、筆記型電腦、安全系統、空間站等。
SMPS 的型別
SMPS 是開關電源電路,設計用於從非穩壓直流或交流電壓獲得穩壓直流輸出電壓。SMPS 主要有四種類型,例如
- 直流-直流轉換器
- 交流-直流轉換器
- 反激式轉換器
- 正激式轉換器
輸入部分中的交流-直流轉換部分使交流-直流轉換器與直流-直流轉換器有所不同。反激式轉換器用於低功率應用。SMPS 型別中還有降壓轉換器和升壓轉換器,它們根據需要降低或提高輸出電壓。其他型別的 SMPS 包括自激反激式轉換器、降壓-升壓轉換器、Cuk、Sepic 等。