電子電路 - 整流器

無論何時需要將交流電轉換為直流電，整流電路都能派上用場。一個簡單的 PN 結二極體就可以充當整流器。二極體的正向偏置和反向偏置條件實現了整流。

整流

交流電具有持續改變其狀態的特性。這可以透過觀察正弦波來理解，正弦波表示交流電。它在正方向上升，達到正峰值，然後從那裡下降到正常值，然後再次進入負方向，達到負峰值，然後再次回到正常值，如此迴圈。

在其波形形成過程中，我們可以觀察到波形在正負方向變化。實際上它完全交替變化，因此得名交流電。

但在整流過程中，這種交流電被轉換成直流電 DC。在此之前，在正負方向流動的波形，在轉換為直流電時，其方向將被限制在正方向。因此，電流只允許在正方向流動，而在負方向被阻擋，如下圖所示。

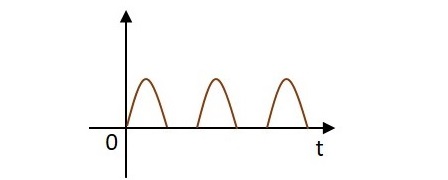
進行整流的電路稱為整流電路。二極體用作整流器，以構建整流電路。

整流電路的型別

根據其輸出，整流電路主要分為兩種型別：

半波整流器
全波整流器

半波整流電路只整流輸入電源的正半周，而全波整流電路則整流輸入電源的正負半周。

半波整流器

半波整流器的名稱本身就表明整流只針對半個週期進行。交流訊號透過輸入變壓器，根據使用情況進行升壓或降壓。在整流電路中，大多使用降壓變壓器，以降低輸入電壓。

輸入到變壓器的訊號透過充當整流器的 PN 結二極體。該二極體僅將交流電壓轉換為輸入正半周的脈動直流電。負載電阻連線在電路的末端。下圖顯示了半波整流器的電路圖。

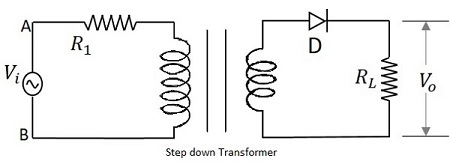
半波整流器的執行原理

輸入訊號輸入到變壓器，降低電壓電平。來自變壓器的輸出輸入到充當整流器的二極體。該二極體在輸入訊號的正半周導通（導電）。因此，電流流過電路，負載電阻兩端將存在電壓降。二極體在負半周截止（不導電），因此負半周的輸出為，$i_{D} = 0$ 和 $V_{o}=0$。

因此，輸出僅存在於輸入電壓的正半周（忽略反向漏電流）。該輸出將是跨負載電阻的脈動輸出。

半波整流器的波形

輸入和輸出波形如下圖所示。

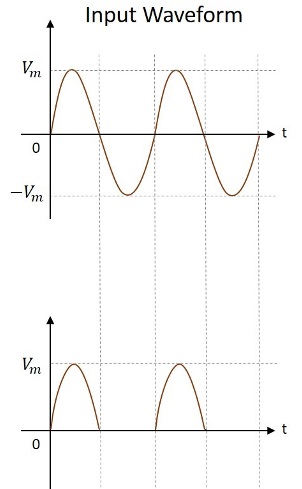
因此，半波整流器的輸出是脈動直流電。讓我們嘗試通過了解從半波整流器輸出獲得的一些值來分析上述電路。

半波整流器的分析

為了分析半波整流電路，讓我們考慮輸入電壓方程。

$$v_{i}=V_{m} \sin \omega t$$

$V_{m}$ 是電源電壓的最大值。

讓我們假設二極體是理想的。

正向電阻，即導通狀態下的電阻為 $R_f$。
反向電阻，即截止狀態下的電阻為 $R_r$。

二極體或負載電阻 $R_L$ 中的電流 i 為

$i=I_m \sin \omega t \quad for\quad 0\leq \omega t\leq \pi$

$ i=0 \quad\quad\quad\quad for \quad \pi\leq \omega t\leq 2 \pi$

其中

$$I_m= \frac{V_m}{R_f+R_L}$$

直流輸出電流

平均電流 $I_{dc}$ 為

$$I_{dc}=\frac{1}{2 \pi}\int_{0}^{2 \pi} i \:d\left ( \omega t \right )$$

$$=\frac{1}{2 \pi}\left [ \int_{0}^{\pi}I_m \sin \omega t \:d\left ( \omega t \right )+\int_{\pi}^{2 \pi}0\: d\left ( \omega t \right )\right ]$$

$$=\frac{1}{2 \pi}\left [ I_m\left \{-\cos \omega t \right \}_{0}^{\pi} \right ]$$

$$=\frac{1}{2 \pi}\left [ I_m\left \{ +1-\left ( -1 \right ) \right \} \right ]=\frac{I_m}{\pi}=0.318 I_m$$

代入 $I_m$ 的值，我們得到

$$I_{dc}=\frac{V_m}{\pi\left ( R_f+R_L \right )}$$

如果 $R_L >> R_f$，則

$$I_{dc}=\frac{V_m}{\pi R_L}=0.318 \frac{V_m}{R_L}$$

直流輸出電壓

直流輸出電壓為

$$ V_{dc}=I_{dc}\times R_L=\frac{I_m}{\pi}\times R_L$$

$$=\frac{V_m\times R_L}{\pi\left (R_f+R_L \right )}=\frac{V_m}{\pi\left \{ 1+\left ( R_f/R_L \right ) \right \}}$$

如果 $R_L>>R_f$，則

$$V_{dc}=\frac{V_m}{\pi}=0.318 V_m$$

有效值電流和電壓

有效值電流為

$$I_{rms}=\left [ \frac{1}{2 \pi}\int_{0}^{2\pi} i^{2} d\left ( \omega t \right )\right ]^{\frac{1}{2}}$$

$$I_{rms}=\left [ \frac{1}{2 \pi}\int_{0}^{\pi}I_{m}^{2} \sin^{2}\omega t \:d\left (\omega t \right ) +\frac{1}{2\pi}\int_{\pi}^{2\pi} 0 \:d\left ( \omega t \right )\right ]^{\frac{1}{2}}$$

$$=\left [ \frac{I_{m}^{2}}{2 \pi}\int_{0}^{\pi}\left ( \frac{1-\cos 2 \omega t}{2} \right )d\left ( \omega t \right ) \right ]^{\frac{1}{2}}$$

$$=\left [ \frac{I_{m}^{2}}{4 \pi}\left \{ \left ( \omega t \right )-\frac{\sin 2 \omega t}{2} \right \}_{0}^{\pi}\right ]^{\frac{1}{2}}$$

$$=\left [ \frac{I_{m}^{2}}{4 \pi}\left \{ \pi - 0 - \frac{\sin 2 \pi}{2}+ \sin 0 \right \} \right ]^{\frac{1}{2}}$$

$$=\left [ \frac{I_{m}^{2}}{4} \right ]^{\frac{1}{2}}=\frac{I_m}{2}$$

$$=\frac{V_m}{2\left ( R_f+R_L \right )}$$

負載上的有效值電壓為

$$V_{rms}=I_{rms} \times R_L= \frac{V_m \times R_L}{2\left ( R_f+R_L \right )}$$

$$=\frac{V_m}{2\left \{ 1+\left ( R_f/R_L \right ) \right \}}$$

如果 $R_L>>R_f$，則

$$V_{rms}=\frac{V_m}{2}$$

整流效率

任何電路都需要在工作中高效才能獲得更好的輸出。要計算半波整流器的效率，必須考慮輸出功率與輸入功率的比率。

整流效率定義為

$$\eta =\frac{直流功率輸送到負載}{交流輸入功率來自變壓器次級}=\frac{P_{dc}}{P_{ac}}$$

現在

$$P_{dc}=\left ( {I_{dc}} \right )^2 \times R_L=\frac{I_m^2 R_L}{\pi^2}$$

此外

其中

$$P_{ac}=P_a+P_r$$

$P_a = 二極體結點上的功耗$

$$=I_{rms}^{2}\times R_f=\frac{I_{m}^{2}}{4}\times R_f$$

和

$$P_r = 負載電阻中的功耗$$

$$=I_{rms}^{2}\times R_L=\frac{I_{m}^{2}}{4}\times R_L$$

$$P_{ac}=\frac{I_{m}^{2}}{4}\times R_f+\frac{I_{m}^{2}}{4}\times R_L =\frac{I_{m}^{2}}{4}\left ( R_f+R_L \right )$$

從 $P_{ac}$ 和 $P_{dc}$ 的兩個表示式，我們可以寫出

$$\eta =\frac{I_{m}^{2}R_L/\pi^2}{I_{m}^{2}\left ( R_f+R_L \right )/4}=\frac{4}{\pi^2}\frac{R_L}{\left ( R_f+R_L \right )}$$

$$=\frac{4}{\pi^2}\frac{1}{\left \{ 1+\left ( R_f/R_L \right ) \right \}}=\frac{0.406}{\left \{ 1+\left ( R_f/R_L \right ) \right \}}$$

整流效率百分比

$$\eta =\frac{40.6}{\lbrace1+\lgroup\: R_{f}/R_{L}\rgroup\rbrace}$$

理論上，當 $R_{f}/R_{L} = 0$ 時，半波整流器的最大整流效率為 40.6%。

此外，效率可以按如下方式計算：

$$\eta =\frac{P_{dc}}{P_{ac}}=\frac{\left (I_{dc} \right )^2R_L}{\left ( I_{rms} \right )^2R_L}=\frac{\left ( V_{dc}/R_L \right )^2R_L}{\left (V_{rms}/R_L \right )^2R_L} =\frac{\left ( V_{dc} \right )^2}{\left ( V_{rms} \right )^2}$$

$$=40.6\%$$

$$=\frac{\left ( V_m/ \pi \right )^2}{\left ( V_m/2 \right )^2}=\frac{4}{\pi^2}=0.406$$

紋波係數

整流輸出包含一定量的交流分量，以紋波的形式存在。這可以透過觀察半波整流器的輸出波形來理解。為了獲得純直流電，我們需要了解這個分量。

紋波係數表示整流輸出的波動程度。用γ表示。這可以定義為電壓或電流的交流分量的有效值與直流值或平均值的比率。

$$\gamma =\frac{紋波電壓}{直流電壓} =\frac{交流分量的有效值}{波形的直流值}=\frac{\left ( V_r \right )_{rms}}{v_{dc}}$$

這裡，

$$\left ( V_r \right )_{rms}=\sqrt{V_{rms}^{2}-V_{dc}^{2}}$$

因此，

$$\gamma =\frac{\sqrt{V_{rms}^{2}-V_{dc}^{2}}}{V_{dc}}=\sqrt{\left (\frac{V_{rms}}{V_{dc}} \right )^2-1}$$

現在，

$$V_{rms}=\left [ \frac{1}{2\pi}\int_{0}^{2\pi} V_{m}^{2} \sin^2\omega t\:d\left ( \omega t \right ) \right ]^{\frac{1}{2}}$$

$$=V_m\left [ \frac{1}{4\pi} \int_{0}^{\pi}\left ( 1- \cos2 \:\omega t \right )d\left ( \omega t \right )\right ]^{\frac{1}{2}}=\frac{V_m}{2}$$

$$V_{dc}=V_{av}=\frac{1}{2\pi}\left [ \int_{0}^{\pi}V_m \sin \omega t \:d\left ( \omega t \right )+\int_{\pi}^{2\pi} 0.d\left ( \omega t \right )\right ]$$

$$=\frac{V_m}{2 \pi}\left [ -\cos \omega t \right ]_{0}^{\pi}=\frac{V_m}{\pi}$$

$$\gamma =\sqrt{\left [ \left \{ \frac{\left ( V_m/2 \right )}{\left ( V_m/\pi \right )} \right \}^2-1 \right ]}=\sqrt{\left \{ \left ( \frac{\pi}{2} \right )^2-1 \right \}}=1.21$$

紋波係數也定義為

$$\gamma =\frac{\left ( I_r \right )_{rms}}{I_{dc}}$$

由於半波整流器中存在的紋波係數為 1.21，這意味著輸出中存在的交流電量為直流電壓的 121%。

穩壓

負載電流可能根據負載電阻而變化。但即使在這種情況下，我們也希望跨負載電阻獲得的輸出電壓保持恆定。因此，即使在不同的負載條件下，我們的電壓也需要進行調節。

直流輸出電壓隨直流負載電流變化的變化定義為穩壓。穩壓百分比計算如下。

$$穩壓百分比=\frac{空載電壓-滿載電壓}{滿載電壓} \times 100\%$$

穩壓百分比越低，電源越好。理想電源的穩壓百分比為零。

變壓器利用率

在整流電路中，要輸送到負載的直流功率決定了電路中使用的變壓器的額定值。

因此，變壓器利用率定義為

$$TUF=\frac{要輸送到負載的直流功率}{變壓器次級的交流額定值}$$

$$=\frac{P_{d.c}}{P_{a.c\left ( rated \right )}}$$

根據變壓器理論，次級的額定電壓為

$$V_m/\sqrt{2}$$

實際流過它的有效值電壓為

$$I_m/2$$

因此

$$TUF=\frac{\left ( I_m/\pi \right )^2\times R_L}{\left ( V_m/\sqrt{2} \right )\times\left ( I_m/2 \right )}$$

但是

$$I_m/2$$

$$V_m=I_m\left ( R_f+R_L \right )$$

$$TUF=\frac{\left ( I_m/\pi \right )^2\times R_L}{\left \{ I_m\left ( R_f+R_L \right )/\sqrt{2} \right \}\times \left ( I_m/2 \right )}$$

$$=\frac{2\sqrt{2}}{\pi^2}\times \frac{R_L}{\left ( R_f+R_L \right )}$$

如果 $R_L>>R_f$，則

反向偏置連線的二極體，應在受控的電壓水平下工作。如果超過安全電壓，二極體將會損壞。因此，瞭解該最大電壓非常重要。

二極體在不被破壞的情況下所能承受的最大反向電壓稱為峰值反向電壓，簡稱PIV。

這裡的PIV就是Vm。

波形因子

這可以理解為波形上所有點的絕對值的數學平均值。波形因子定義為有效值與平均值的比率。用F表示。

$$F=\frac{有效值}{平均值}=\frac{I_m/2}{I_m/\pi}=\frac{0.5I_m}{0.318I_m}=1.57$$

峰值因子

必須考慮波紋中的峰值，才能知道整流的效果如何。峰值因子的值也是一個重要的考慮因素。峰值因子定義為峰值與有效值的比率。

$$I_m/2$$

$$峰值因子=\frac{峰值}{有效值}=\frac{V_m}{V_m/2}=2$$

所有這些都是研究整流器時需要考慮的重要引數。

列印頁面