
- 電子電路資源
- 電子電路 - 快速指南
- 電子電路 - 資源
- 電子電路 - 討論
電子電路 - 訊號
訊號可以理解為“表示從產生它的源頭存在的資料資訊的表示”。這通常是隨時間變化的。因此,訊號可以是傳輸資訊的能量源。這很容易用圖表表示。
示例
- 鬧鐘發出訊號表示時間到了。
- 高壓鍋的哨聲確認食物已煮熟。
- 紅燈表示危險。
- 交通訊號燈指示你的行動。
- 電話鈴聲表示有你的來電。
訊號可以是任何型別的傳遞資訊的載體。從電子裝置產生的這種訊號稱為電子訊號或電訊號。這些通常是隨時間變化的。
訊號型別
根據其特性,訊號可以分為模擬訊號和數字訊號。模擬訊號和數字訊號可以進一步分類,如下面的影像所示。

模擬訊號
表示隨時間變化的量的連續時間變化訊號,可以稱為模擬訊號。該訊號會根據表示它的量的瞬時值隨時間不斷變化。
數字訊號
本質上是離散的或形式上非連續的訊號可以稱為數字訊號。該訊號具有單獨表示的各個值,這些值不基於先前的值,就好像它們是在該特定時刻匯出的。
週期訊號和非週期訊號
任何在一段時間內重複其模式的模擬或數字訊號,都稱為週期訊號。該訊號的模式重複出現,很容易假設或計算。
任何在一段時間內不重複其模式的模擬或數字訊號,都稱為非週期訊號。該訊號的模式持續存在,但模式不重複,因此不容易假設或計算。
訊號和符號
在週期訊號中,最常用的訊號是正弦波、餘弦波、三角波、方波、矩形波、鋸齒波、脈衝波或脈衝序列等。讓我們來看看這些波形。
單位階躍訊號
單位階躍訊號從其原點到X軸上的一個單位的值為一個單位。這主要用作測試訊號。單位階躍訊號的影像如下所示。

單位階躍函式用$u\left ( t \right )$表示。其定義為:
$$u\left ( t \right )=\left\{\begin{matrix}1 & t\geq 0\\ 0 & t< 0\end{matrix}\right.$$
單位衝激訊號
單位衝激訊號在其原點處的值為一個單位。其面積為一個單位。單位衝激訊號的影像如下所示。

單位衝激函式用ẟ(t)表示。其定義為
$$\delta \left ( t \right )=\left\{\begin{matrix} \infty \:\:如果\:\:t=0\\0 \:\:如果\:\:t\neq 0\end{matrix}\right.$$
$$\int_{-\infty }^{\infty }\delta \left ( t \right )d\left ( t \right )=1$$
$$\int_{-\infty }^{t }\delta \left ( t \right )d\left ( t \right )=u\left ( t \right )$$
$$\delta \left ( t \right )=\frac{du\left ( t \right )}{d\left ( t \right )} $$
單位斜坡訊號
單位斜坡訊號的值從其原點開始呈指數增長。單位斜坡訊號的影像如下所示。
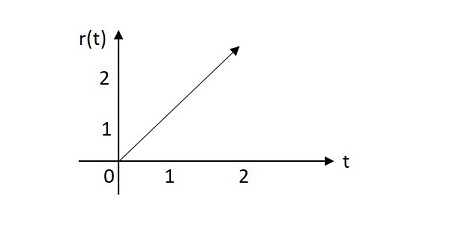
單位斜坡函式用u(t)表示。其定義為:
$$\int_{0}^{t}u\left ( t \right ) d\left ( t \right )=\int_{0}^{t} 1 dt =t=r\left ( t \right )$$
$$u\left ( t \right )=\frac{dr\left ( t \right )}{dt}$$
單位拋物線訊號
單位拋物線訊號的值在其原點處像拋物線一樣變化。單位拋物線訊號的影像如下所示。

單位拋物線函式用$u\left ( t \right )$表示。其定義為:
$$\int_{0}^{t}\int_{0}^{t}u\left ( t \right )dtdt=\int_{0}^{t}r\left ( t \right )dt=\int_{0}^{t} t.dt=\frac{t^{2}}{2}dt=x\left ( t \right )$$
$$r\left ( t \right )=\frac{dx\left ( t \right )}{dt}$$
$$u\left ( t \right )=\frac{d^{2}x\left ( t \right )}{dt^{2}}$$
符號函式
符號函式的值從其原點在正負平面均等分佈。符號函式的影像如下所示。
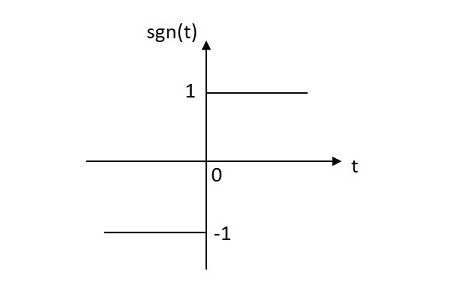
符號函式用sgn(t)表示。其定義為
$$sgn\left ( t \right )=\left\{\begin{matrix} 1 \:\: 對於 \:\: t\geq 0\\-1 \:\: 對於 \:\:t < 0\end{matrix}\right.$$
$$sgn\left ( t \right )=2u\left ( t \right ) -1$$
指數訊號
指數訊號的值從其原點呈指數變化。指數函式的形式為:
$$x\left ( t \right ) =e^{\alpha t}$$
指數的形狀由$\alpha$決定。此函式可以在三種情況下理解
情況1:
如果$\alpha = 0\rightarrow x\left ( t \right )=e^{0}=1$
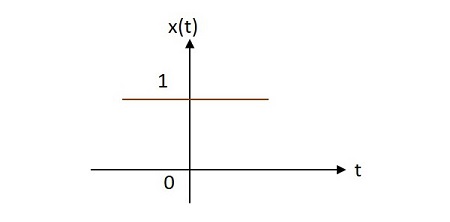
情況2:
如果$\alpha <0$,則$x\left ( t \right )=e^{\alpha t}$,其中$\alpha$為負數。此形狀稱為衰減指數。

情況3:
如果$\alpha > 0$,則$x\left ( t \right )=e^{\alpha t}$,其中$\alpha$為正數。此形狀稱為增長指數。
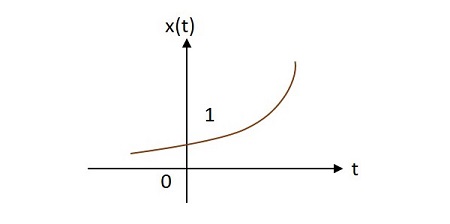
矩形訊號
矩形訊號的值在其原點處在正負平面呈矩形分佈。矩形訊號的影像如下所示。

矩形函式用$x\left ( t \right )$表示。其定義為
$$x\left ( t \right )=A \:rect\left [ \frac{t}{T} \right ]$$
三角訊號
矩形訊號的值在其原點處在正負平面呈三角形分佈。三角訊號的影像如下所示。

三角函式用$x\left ( t \right )$表示。其定義為
$$x\left ( t \right )=A \left [ 1-\frac{\left | t \right |}{T} \right ]$$
正弦訊號
正弦訊號的值從其原點呈正弦變化。正弦訊號的影像如下所示。
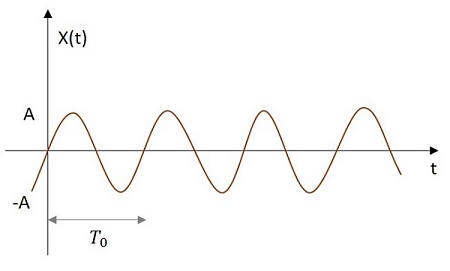
正弦函式用x(t)表示。其定義為:
$$x\left ( t \right )=A \cos \left ( w_{0} t\pm \phi \right )$$
或
$$x\left ( t \right )=A sin\left ( w_{0}t\pm \phi \right )$$
其中$T_{0}=\frac{2 \pi}{w_{0}}$
Sinc函式
Sinc訊號的值根據如下給出的特定關係變化。它在原點處具有最大值,並隨著遠離原點而逐漸減小。Sinc函式訊號的影像如下所示。
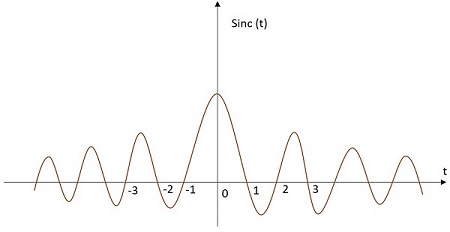
Sinc函式用sinc(t)表示。其定義為:
$$sinc\left ( t \right )=\frac{sin\left ( \pi t \right )}{\pi t}$$
因此,這些是我們經常在電子和通訊領域遇到的不同訊號。每個訊號都可以用數學方程來定義,以使訊號分析更容易。
每個訊號都有前面提到的特定波形。波形的整形可能會改變訊號中存在的內容。無論如何,由設計工程師決定是否要為任何特定電路改變波形。但是,要改變波形的形狀,有一些技術將在後續單元中討論。