資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法學電力牽引：驅動軸的功率輸出和能量輸出
驅動軸的功率輸出
設：
𝐹𝑡 = 牽引力 (牛頓)
𝑉 = 火車速度 (公里/小時)
由於功率輸出定義為單位時間內完成的功，即：
$$\mathrm{功率輸出,\mathit{P}\mathrm{\: =\: }單位時間內完成的功\mathrm{\: =\: }\frac{功}{時間}}$$
$$\mathrm{\Rightarrow \mathit{P}\mathrm{\: =\: }\frac{牽引力\times 距離}{時間}\mathrm{\: =\: }牽引力\times 速度}$$
$$\mathrm{\therefore \mathit{P\mathrm{\: =\: }F_{t}\times V}\: Nm/s}$$
$$\mathrm{\Rightarrow \mathit{P\mathrm{\: =\: }F_{t}\times V}\times \frac{1000}{3600}\, 瓦特}$$
$$\mathrm{\therefore \mathit{P\mathrm{\: =\: }\frac{F_{t}\times V}{\mathrm{3600}}}\: 千瓦\: \cdot \cdot \cdot \left ( 1 \right )}$$
現在，如果𝜼是齒輪傳動的效率，則電動機的功率輸出（或驅動軸的功率輸入）由下式給出：
$$\mathrm{功率輸入,\mathit{P_{i}\mathrm{\: =\: }\frac{F_{t}\times V}{\eta }}\: 瓦特\: \cdot \cdot \cdot \left ( 2 \right )}$$
$$\mathrm{\Rightarrow \mathit{P_{i}\mathrm{\: =\: }\frac{F_{t}\times V}{\mathrm{3600\eta }}}\: 千瓦\: \cdot \cdot \cdot \left ( 3 \right )}$$
驅動軸的能量輸出
假設電力火車執行遵循簡化的梯形速度-時間曲線。
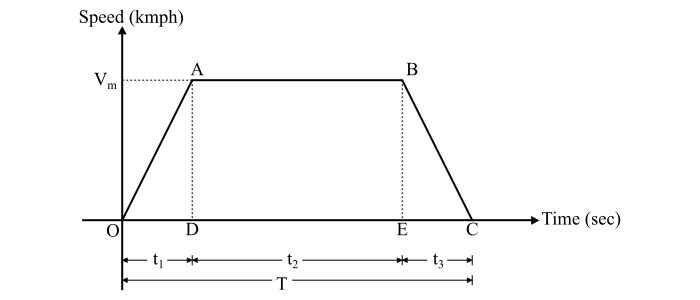
那麼，執行所需的總能量（或驅動軸的能量輸出）由下式給出：
$$\mathrm{總能量\mathrm{\: =\: }加速階段所需的能量\mathrm{\: +\: }勻速執行階段所需的能量}$$
$$\mathrm{\Rightarrow 總能量\mathrm{\: =\: }加速階段的平均功率\times 加速時間\mathrm{\: +\: }勻速執行階段的平均功率 \times 勻速執行時間}$$
從圖中，我們有：
$$\mathrm{總能量\mathrm{\: =\: }\frac{1}{2}\frac{\mathit{F_{t}\times V_{m}}}{\mathrm{3600}}\times \frac{\mathit{t_{\mathrm{1}}}}{3600}\mathrm{\: +\: }\frac{\mathit{F_{t}^{'}V_{m}}}{3600}\mathrm{\: +\: }\frac{\mathit{t_{\mathrm{2}}}}{3600}\: \: 千瓦時 …(4)}$$
其中：
𝑽𝒎 為火車的最大速度 (公里/小時)。
𝑭𝒕 為加速階段所需的牽引力 (牛頓)
𝑭𝒕′ 為勻速執行階段所需的牽引力 (牛頓)
𝒕1 為加速時間 (秒)
𝒕2 為勻速執行時間 (秒)
在實踐中，驅動軸的能量輸出或執行所需的總能量以瓦特小時/噸公里表示，而不是千瓦時。因此：
$$\mathrm{\mathrm{\: =\: }\frac{能量輸出（瓦特小時）}{火車重量（噸）\times 執行距離（公里）} \: \: \: \cdot \cdot \cdot \left ( 5 \right )}$$
公式 (5) 給出的量稱為驅動軸的比能量輸出。
數值例子 (1)
一輛重 100 噸的電力火車需要以 35 公里/小時的速度駛上 2% 的斜坡。如果此速度下的火車阻力為每噸 1 公斤，則求驅動軸的功率輸出。
解答
已知資料：
火車重量，𝑊 = 100 噸
坡度，𝐺 = 2%
火車的單位阻力，𝑟 = 每噸 1 公斤
速度，𝑉 = 35 公里/小時
因此，所需的牽引力為：
$$\mathrm{\mathit{F_{t}\mathrm{\: =\: }\mathrm{98.1}WG\mathrm{\: +\: }Wrg}} $$
$$\mathrm{\Rightarrow \mathit{F_{t}}\mathrm{\: =\: }98.1\times 100\times 2\mathrm{\: +\: }100\times 1\times 9.81\mathrm{\: =\: }20601\: 牛頓} $$
$$\mathrm{\therefore 驅動軸的功率輸出,\: \mathit{P\mathrm{\: =\: }\frac{F_{t}\times V}{\mathrm{3600}}}\mathrm{\: =\: }\frac{20601\times 35}{3600}} $$
$$\mathrm{\mathit{P}\mathrm{\: =\: }200.29 \: 千瓦} $$
數值例子 (2)
計算一輛重 100 噸的火車的比能量輸出，已知最大速度為 46 公里/小時，給定執行距離為 1.5 公里，加速階段的牽引力為 9810 牛頓，加速時間為 30 秒。勻速執行階段所需的牽引力為 981 牛頓，勻速執行時間為 73 秒。假設速度-時間曲線為梯形。
解答
已知資料：
最大速度，𝑉𝑚 = 46 公里/小時
行駛距離，𝑆 = 1.5 公里
加速階段的牽引力，𝐹𝑡 = 9810 牛頓
勻速執行階段的牽引力，𝐹𝑡′ = 981 牛頓
加速時間，𝑡1 = 30 秒
勻速執行時間，𝑡2 = 73 秒
現在，能量輸出（以瓦特小時表示）由下式給出：
$$\mathrm{\mathrm{\: =\: }\frac{1}{2}\frac{\mathit{F_{t}\times V_{m}}}{\mathrm{3600}}\times \frac{\mathit{t_{\mathrm{1}}}}{3600}\mathrm{\: +\: }\frac{\mathit{F_{t}^{'}V_{m}}}{3600}\mathrm{\: +\: }\frac{\mathit{t_{\mathrm{2}}}}{3600}}$$
$$\mathrm{\mathrm{\: =\: }\frac{1}{2}\times \frac{9810\times 46}{3600}\times \frac{30}{3600}\mathrm{\: +\: }\frac{981\times 46}{3600}\times \frac{73}{3600}\mathrm{\: =\: }0.5223\mathrm{\: +\: }0.2542\mathrm{\: =\: }0.7765 \: 千瓦時}$$
$$\mathrm{\therefore 能量輸出（瓦特小時）\mathrm{\: =\: }776.5 \, 瓦特小時}$$
因此，比能量輸出由下式給出：
$$\mathrm{\mathrm{\: =\: }\frac{能量輸出（瓦特小時）}{火車重量（噸）\times 執行距離（公里）}}$$
$$\mathrm{\mathrm{\: =\: }\frac{776.5}{100\times 1.5}\mathrm{\: =\: }5.17\: 瓦特/噸公里}$$
1K+ 次瀏覽
