資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝學
法學電力牽引：四邊形速度時間曲線
對於城市和郊區服務，電力牽引的簡化四邊形速度時間曲線如圖所示。
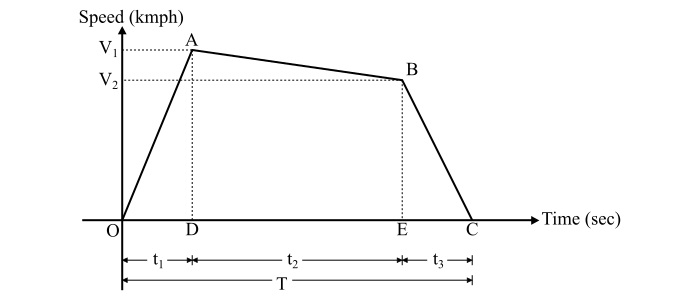
設：
$\alpha$ = 加速度 (km/h/s)
$\beta$ = 制動減速度 (km/h/s)
$\beta_{c}$ = 滑行減速度 (km/h/s)
V1 = 加速結束時的最大速度 (km/h)
V2 = 滑行結束時的速度 (km/h)
T = 總執行時間 (秒)
t1 = 加速時間 (秒)
t2 = 滑行時間 (秒)
t3 = 制動時間 (秒)
D = 總行駛距離 (km)
因此，加速時間由下式給出：
$$\mathrm{\mathit{t_{\mathrm{1}}}\:=\:\frac{\mathit{V_{\mathrm{1}}}}{\alpha } }$$
滑行時間由下式給出：
$$\mathrm{\mathit{t_{\mathrm{2}}}\:=\:\frac{\mathit{V_{\mathrm{1}}}-\mathit{V_{\mathrm{2}}}}{\beta_{c} } \:\:\:\cdot \cdot \cdot \mathrm{\left ( \mathrm{1} \right )}}$$
制動時間由下式給出：
$$\mathrm{\mathit{t_{\mathrm{3}}}\:=\:\frac{\mathit{V_{\mathrm{2}}}}{\beta }}$$
現在，總行駛距離 (km) 為：
$$\mathrm{\mathit{D}\:=\:\mathrm{加速行駛距離\:+\:滑行行駛距離\:+\:制動行駛距離}}$$
$$\mathrm{\Rightarrow \mathit{D}\:=\:\mathrm{△OAD面積\:+\:四邊形DABE面積\:+\:△CEB面積}}$$
$$\mathrm{\Rightarrow \mathit{D}\:=\:\mathrm{\left (\frac{1}{2}\times \mathit{V_{\mathrm{1}}}\times \frac{\mathit{t_{\mathrm{1}}}}{3600} \right )}\:+\:\mathrm{\left ( \frac{\mathit{V_{\mathrm{1}}}+\mathit{V_{\mathrm{2}}}}{2}\times \frac{\mathit{t_{\mathrm{2}}}}{3600} \right )}\:+\:\mathrm{\left (\frac{1}{2}\times \mathit{V_{\mathrm{2}}}\times \frac{\mathit{t_{\mathrm{3}}}}{3600} \right )}}$$
$$\mathrm{\Rightarrow \mathit{D}\:=\:\frac{\mathit{V_{\mathrm{1}}\mathit{t_{\mathrm{1}}}}}{7200}\:+\:\frac{\mathit{V_{\mathrm{1}}\mathit{t_{\mathrm{2}}}}}{7200}\:+\:\frac{\mathit{V_{\mathrm{2}}\mathit{t_{\mathrm{2}}}}}{7200}\:+\:\frac{\mathit{V_{\mathrm{2}}\mathit{t_{\mathrm{3}}}}}{7200}}$$
$$\mathrm{\Rightarrow \mathit{D}\:=\:\frac{\mathit{V_{\mathrm{1}}}}{7200}\mathrm{\left ( \mathit{t_{\mathrm{1}}+\mathit{t_{\mathrm{2}}}} \right )}\:+\:\frac{\mathit{V_{\mathrm{2}}}}{7200}\mathrm{\left ( \mathit{t_{\mathrm{2}}+\mathit{t_{\mathrm{3}}}} \right )}}$$
$$\mathrm{\because \mathit{T}\:=\:\mathit{t_{\mathrm{1}}}\:+\:\mathit{t_{\mathrm{2}}}\:+\:\mathit{t_{\mathrm{3}}}}$$
$$\mathrm{\Rightarrow \mathit{t_{\mathrm{1}}}\:+\:\mathit{t_{\mathrm{2}}}\:=\:\mathit{T-\mathit{t_{\mathrm{3}}}}\:\mathrm{and}\:\mathit{t_{\mathrm{2}}}\:+\:\mathit{t_{\mathrm{3}}}\:=\:\mathit{T-\mathit{t_{\mathrm{1}}}}}$$
$$\mathrm{\therefore \mathit{D}\:=\:\frac{\mathit{V_{\mathrm{1}}}}{7200}\mathrm{\left ( \mathit{T-\mathit{t_{\mathrm{3}}}} \right )}\:+\:\frac{\mathit{V_{\mathrm{2}}}}{7200}\mathrm{\left ( \mathit{T-\mathit{t_{\mathrm{1}}}} \right )}}$$
$$\mathrm{\Rightarrow \mathit{D}\:=\:\frac{\mathit{T}}{7200}\mathrm{\left ( \mathit{V_{\mathrm{1}}+\mathit{V_{\mathrm{2}}}} \right )}\:-\:\frac{\mathit{V_{\mathrm{1}}t_{\mathrm{3}}}}{7200}\:-\:\frac{\mathit{V_{\mathrm{2}}t_{\mathrm{1}}}}{7200}}$$
代入t1和t3的值，得到：
$$\mathrm{\Rightarrow \mathit{D}\:=\:\frac{\mathit{T}}{7200}\mathrm{\left ( \mathit{V_{\mathrm{1}}+\mathit{V_{\mathrm{2}}}} \right )}\:-\frac{\mathit{V_{\mathrm{1}}\mathit{V_{\mathrm{2}}}}}{7200\beta }\:-\:\frac{\mathit{V_{\mathrm{1}}\mathit{V_{\mathrm{2}}}}}{7200\alpha }}$$
$$\mathrm{\Rightarrow 7200\mathit{D}\:=\:\mathit{T}\mathrm{\left ( \mathit{V_{\mathrm{1}}+\mathit{V_{\mathrm{2}}}} \right )}-\mathit{V_{\mathrm{1}}\mathit{V_{\mathrm{2}}}}\mathrm{\left ( \frac{1}{\alpha }\:+\:\frac{1}{\beta } \right )}\:\:\:\cdot \cdot \cdot \mathrm{\left ( 2 \right )}}$$
現在，重新排列方程 (1)，得到：
$$\mathrm{\mathit{V_{\mathrm{2}}}\:=\:\mathit{V_{\mathrm{1}}}-\beta _{c}\mathit{t_{\mathrm{2}}}}$$
$$\mathrm{\Rightarrow \mathit{V_{\mathrm{2}}}\:=\:\mathit{V_{\mathrm{1}}}-\beta _{c}\mathrm{\left ( \mathit{T-\mathit{t_{\mathrm{1}}-t_{\mathrm{3}}}} \right )}\:=\:\mathit{V_{\mathrm{1}}}-\beta _{c}\mathrm{\left ( \mathit{T-\frac{\mathit{V_{\mathrm{1}}}}{\alpha }-\frac{\mathit{V_{\mathrm{2}}}}{\beta }} \right )}}$$
$$\mathrm{\Rightarrow \mathit{V_{\mathrm{2}}}-\frac{\beta _{c}\mathit{V_{\mathrm{2}}}}{\beta }\:=\:\mathit{V_{\mathrm{1}}}-\beta _{c}\mathrm{\left ( \mathit{T-\frac{\mathit{V_{\mathrm{1}}}}{\alpha }} \right )}}$$
$$\mathrm{\therefore \mathit{V_{\mathrm{2}}}\:=\:\frac{\mathit{V_{\mathrm{1}}}-\beta _{c}\mathit{T}+\frac{\beta _{c}}{\alpha }\mathit{V_{\mathrm{1}}}}{1-\frac{\beta _{c}}{\beta }}\:\:\:\cdot \cdot \cdot \mathrm{\left ( 3 \right )}}$$
因此，透過求解方程 (2) 和 (3)，可以確定D、V1、V2等的值。
數值例子
一輛火車需要在相距1.5公里的兩個車站之間執行，平均速度為50公里/小時。執行採用簡化的四邊形速度時間曲線。如果最大速度限制為60公里/小時，加速度為2公里/小時/秒，滑行和制動減速度分別為0.15公里/小時/秒和3公里/小時/秒，並且在施加制動器之前的火車速度為48公里/小時。確定加速、滑行和制動的持續時間。
解答
已知：
執行距離，D = 1.5 公里
平均速度，Vα = 50 公里/小時
最大速度，V1 = 60 公里/小時
滑行結束時的速度，V2 = 48 公里/小時
加速度，α = 2 公里/小時/秒
滑行減速度，βc = 0.15 公里/小時/秒
制動減速度，β = 3 公里/小時/秒
因此，加速持續時間為：
$$\mathrm{\mathit{t_{\mathrm{1}}}\:=\:\frac{\mathit{V_{\mathrm{1}}}}{\alpha }\:=\:\frac{60}{2}\:=\:30 \:\mathrm{秒}}$$
滑行持續時間為：
$$\mathrm{\mathit{t_{\mathrm{2}}}\:=\:\frac{\mathit{V_{\mathrm{1}}}-\mathit{V_{\mathrm{2}}}}{\beta_{c} }\:=\:\frac{60-48}{0.15}\:=\:80 \:\mathrm{秒}}$$
而制動持續時間為：
$$\mathrm{\mathit{t_{\mathrm{3}}}\:=\:\frac{\mathit{V_{\mathrm{3}}}}{\beta }\:=\:\frac{48}{3}\:=\:16 \:\mathrm{秒}}$$
5000+ 瀏覽量
