時間複雜度

---

---

本章我們將討論演算法的時間複雜度及其影響因素。

時間複雜度

一般來說，演算法的時間複雜度是指演算法執行程式碼中每條語句所需的時間。它不是演算法的執行時間。這個量會受到多種因素的影響，例如輸入大小、使用的方法和過程。當在儘可能短的時間內產生輸出時，演算法被認為是最有效的。

找到演算法時間複雜度的最常用方法是將演算法推導為遞推關係。讓我們進一步瞭解它。

求解遞推關係

遞推關係是由自身較小輸入定義的方程（或不等式）。這些關係是基於數學歸納法求解的。在這兩個過程中，一個條件允許問題被分解成較小的部分，這些部分使用較低值的輸入執行相同的方程。

這些遞推關係可以使用多種方法求解；它們是：

• 代換法

• 遞迴樹法

• 迭代法

• 主定理

代換法

代換法是一種試錯法；其中，我們可能認為可能是關係解的值被代入並檢查方程是否有效。如果有效，則找到解。否則，檢查另一個值。

步驟

使用代換法求解遞推關係的步驟如下：

• 基於試錯法猜測解的形式

• 使用數學歸納法證明該解對所有情況都正確。

示例

讓我們來看一個使用代換法求解遞推關係的例子：

T(n) = 2T(n/2) + n

這裡，我們假設該方程的時間複雜度為**O(nlogn)**。因此，根據數學歸納法，T(n/2) 的時間複雜度將為**O(n/2logn/2)**；將該值代入給定方程，我們需要證明T(n)必須大於或等於**nlogn**。

≤ 2n/2Log(n/2) + n
= nLogn - nLog2 + n
= nLogn - n + n
≤ nLogn

遞迴樹法

在遞迴樹方法中，我們繪製一個遞迴樹，直到程式無法進一步細分為更小的部分。然後，我們計算遞迴樹每一層所需的時間。

步驟

• 繪製程式的遞迴樹

• 計算每一層的時間複雜度，並將它們加起來以找到總的時間複雜度。

示例

考慮二分查詢演算法併為其構建遞迴樹：

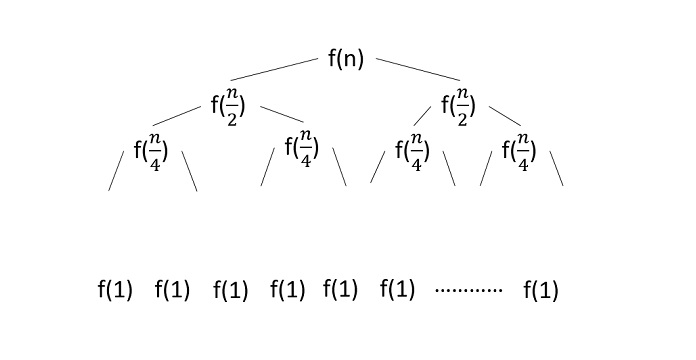
由於該演算法遵循分治策略，因此遞迴樹繪製到它達到最小輸入級別$\mathrm{T\left ( \frac{n}{2^{k}} \right )}$.

$$\mathrm{T\left ( \frac{n}{2^{k}} \right )=T\left ( 1 \right )}$$

$$\mathrm{n=2^{k}}$$

在方程的兩邊應用對數，

$$\mathrm{log\: n=log\: 2^{k}}$$

$$\mathrm{k=log_{2}\:n}$$

因此，二分查詢演算法的時間複雜度為**O(log n)**。

主方法

主方法或主定理應用於遞減或劃分遞推關係以查詢時間複雜度。它使用一組公式來推匯出演算法的時間複雜度。

要了解更多關於主定理的資訊，請點選這裡