最大團

Table of content
上一頁
下一頁

在一個無向圖中，團是一個給定圖的完全子圖。完全子圖意味著這個子圖的所有頂點都連線到這個子圖的所有其他頂點。

最大團問題是尋找圖的最大團的計算問題。最大團用於許多現實世界的問題。

讓我們考慮一個社交網路應用程式，其中頂點代表人們的個人資料，邊代表圖中的相互認識。在這個圖中，團代表一群彼此都認識的人。

為了找到最大團，可以系統地檢查所有子集，但是這種蠻力搜尋對於包含幾十個以上頂點的網路來說過於耗時。

最大團演算法

尋找圖的最大團的演算法相對簡單。該過程的步驟如下：

步驟1：將一個圖作為演算法的輸入，該圖具有非空的頂點集和邊集。

步驟2：建立一個輸出集，如果邊構成圖的團，則將它們新增到輸出集中。

步驟3：迭代地重複步驟2，直到檢查圖的所有頂點，並且列表不再形成團。

步驟4：然後回溯輸出集以檢查哪個團具有最大邊數。

虛擬碼

Algorithm: Max-Clique (G, n, k)
S := ф
for i = 1 to k do
   t := choice (1…n) 
   if t є S then
      return failure
   S := S U t 
for all pairs (i, j) such that i є S and j є S and i ≠ j do
   if (i, j) is not a edge of the graph then 
      return failure
return success

分析

最大團問題是一個非確定性演算法。在這個演算法中，我們首先嚐試確定一組k個不同的頂點，然後我們嘗試測試這些頂點是否構成一個完全圖。

沒有多項式時間確定性演算法可以解決這個問題。這個問題是NP完全的。

示例

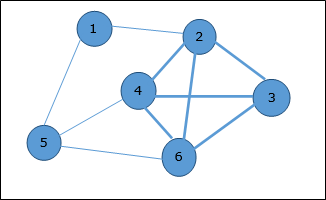
看下面的圖。這裡，包含頂點2、3、4和6的子圖構成一個完全圖。因此，這個子圖是一個團。由於這是所提供圖的最大完全子圖，因此它是一個4-團。

Max Cliques

實現

以下是上述方法在各種程式語言中的實現：

C C++ Java Python
#include <stdio.h>
#define MAX 100
int store[MAX], n;
int graph[MAX][MAX];
int d[MAX];
int max(int a, int b){
   if(a > b){
      return a;
   }
   else{
      return b;
   }
}
int is_clique(int b)
{
   for (int i = 1; i < b; i++) {
      for (int j = i + 1; j < b; j++) {
         if (graph[store[i]][store[j]] == 0) {
            return 0;
         }
      }
   }
   return 1;
}
int maxCliques(int i, int l)
{
   int max_ = 0;
   for (int j = i + 1; j <= n; j++) {
      store[l] = j;
      if (is_clique(l + 1)) {
         max_ = max(max_, l);
         max_ = max(max_, maxCliques(j, l + 1));
      }
   }
   return max_;
}
int main()
{
   int edges[][2] = { { 1, 4 }, { 4, 6 }, { 1, 6 },
                      { 3, 3 }, { 4, 2 }, { 8, 12 } };
   int size = sizeof(edges) / sizeof(edges[0]);
   n = 6;
   for (int i = 0; i < size; i++) {
      graph[edges[i][0]][edges[i][1]] = 1;
      graph[edges[i][1]][edges[i][0]] = 1;
      d[edges[i][0]]++;
      d[edges[i][1]]++;
   }
   printf("Max clique: %d\n", maxCliques(0, 1));
   return 0;
}

輸出

Max clique: 3

using namespace std;
#include<iostream>
const int MAX = 100;
// Storing the vertices
int store[MAX], n;
// Graph
int graph[MAX][MAX];
// Degree of the vertices
int d[MAX];
// Function to check if the given set of vertices in store array is a clique or not
bool is_clique(int b)
{
   // Run a loop for all set of edges
   for (int i = 1; i < b; i++) {
      for (int j = i + 1; j < b; j++)
   
      // If any edge is missing
      if (graph[store[i]][store[j]] == 0)
         return false;
   }
   return true;
}
// Function to find all the sizes of maximal cliques
int maxCliques(int i, int l)
{
   // Maximal clique size
   int max_ = 0;
   // Check if any vertices from i+1 can be inserted
   for (int j = i + 1; j <= n; j++) {
      // Add the vertex to store
      store[l] = j;
      // If the graph is not a clique of size k then
      // it cannot be a clique by adding another edge
      if (is_clique(l + 1)) {
   	     // Update max
   	     max_ = max(max_, l);
   	     // Check if another edge can be added
   	     max_ = max(max_, maxCliques(j, l + 1));
   	}
   }
   return max_;
}
// Driver code
int main()
{
   int edges[][2] = { { 1, 4 }, { 4, 6 }, { 1, 6 },
   				{ 3, 3 }, { 4, 2 }, { 8, 12 } };
   int size = sizeof(edges) / sizeof(edges[0]);
   n = 6;
   for (int i = 0; i < size; i++) {
      graph[edges[i][0]][edges[i][1]] = 1;
      graph[edges[i][1]][edges[i][0]] = 1;
      d[edges[i][0]]++;
      d[edges[i][1]]++;
   }
   cout <<"Max clique: "<<maxCliques(0, 1);
   return 0;
}

輸出

Max clique: 3

import java.util.ArrayList;
import java.util.List;
public class MaxCliques {
   static final int MAX = 100;
   static int[] store = new int[MAX];
   static int[][] graph = new int[MAX][MAX];
   static int[] d = new int[MAX];
   static int n;
   // Function to check if the given set of vertices in store array is a clique or not
   static boolean isClique(int b) {
      for (int i = 1; i < b; i++) {
         for (int j = i + 1; j < b; j++)
            if (graph[store[i]][store[j]] == 0)
               return false;
      }
      return true;
   }
   // Function to find all the sizes of maximal cliques
   static int maxCliques(int i, int l) {
      int max_ = 0;
      for (int j = i + 1; j <= n; j++) {
         store[l] = j;
         if (isClique(l + 1)) {
            max_ = Math.max(max_, l);
            max_ = Math.max(max_, maxCliques(j, l + 1));
         }
      }
      return max_;
   }
   // Driver code
public static void main(String[] args) {
   int[][] edges = { { 1, 4 }, { 4, 6 }, { 1, 6 },
           { 3, 3 }, { 4, 2 }, { 8, 12 } };
   int size = edges.length;
   n = 6;
   for (int i = 0; i < size; i++) {
      graph[edges[i][0]][edges[i][1]] = 1;
      graph[edges[i][1]][edges[i][0]] = 1;
      d[edges[i][0]]++;
      d[edges[i][1]]++;
   }
   System.out.println("Max cliques: " + maxCliques(0, 1));
   }
}

輸出

Max cliques: 3

MAX = 100
# Storing the vertices
store = [0] * MAX
n = 0
# Graph
graph = [[0] * MAX for _ in range(MAX)]
# Degree of the vertices
d = [0] * MAX
# Function to check if the given set of vertices in store array is a clique or not
def is_clique(b):
    # Run a loop for all set of edges
    for i in range(1, b):
        for j in range(i + 1, b):
            # If any edge is missing
            if graph[store[i]][store[j]] == 0:
                return False
    return True
# Function to find all the sizes of maximal cliques
def maxCliques(i, l):
    # Maximal clique size
    max_ = 0
    # Check if any vertices from i+1 can be inserted
    for j in range(i + 1, n + 1):
        # Add the vertex to store
        store[l] = j
        # If the graph is not a clique of size k then
        # it cannot be a clique by adding another edge
        if is_clique(l + 1):
            # Update max
            max_ = max(max_, l)
            # Check if another edge can be added
            max_ = max(max_, maxCliques(j, l + 1))
    return max_
# Driver code
def main():
    global n
    edges = [(1, 4), (4, 6), (1, 6),
             (3, 3), (4, 2), (8, 12)]
    size = len(edges)
    n = 6
    for i in range(size):
        graph[edges[i][0]][edges[i][1]] = 1
        graph[edges[i][1]][edges[i][0]] = 1
        d[edges[i][0]] += 1
        d[edges[i][1]] += 1
    print("Max cliques:" ,maxCliques(0, 1))
if __name__ == "__main__":
    main()

輸出

Max cliques: 3
列印頁面
上一頁
下一頁
廣告