堆排序中的插入操作

Table of content

分析
示例

為了將一個元素插入堆中，新的元素首先被新增到堆的末尾，作為陣列的最後一個元素。

插入此元素後，堆屬性可能被破壞，因此透過將新增的元素與其父元素進行比較並將新增的元素向上移動一級，與父元素交換位置來修復堆屬性。此過程稱為 **向上篩選**。

重複比較，直到父元素大於或等於正在篩選的元素。

Algorithm: Max-Heap-Insert (numbers[], key) 
heapsize = heapsize + 1 
numbers[heapsize] = -∞ 
i = heapsize 
numbers[i] = key 
while i > 1 and numbers[Parent(numbers[], i)] < numbers[i] 
   exchange(numbers[i], numbers[Parent(numbers[], i)]) 
   i = Parent (numbers[], i)

分析

最初，元素被新增到陣列的末尾。如果它違反了堆屬性，則元素將與其父元素交換。樹的高度為 **log n**。最多需要執行 **log n** 次操作。

因此，此函式的複雜度為 **O(log n)**。

示例

讓我們考慮一個最大堆，如下所示，其中需要新增一個新元素 5。

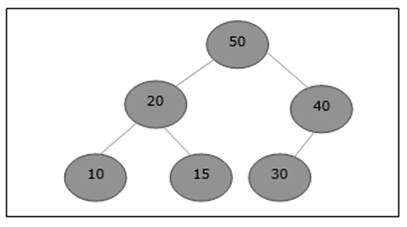
最初，55 將被新增到此陣列的末尾。

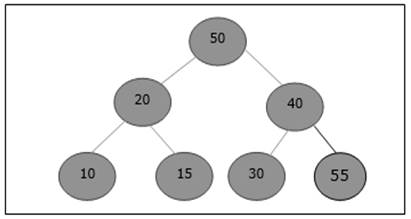
插入後，它違反了堆屬性。因此，需要將元素與其父元素交換。交換後，堆如下所示。

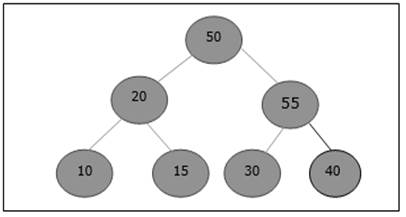
元素再次違反了堆屬性。因此，它與其父元素交換。

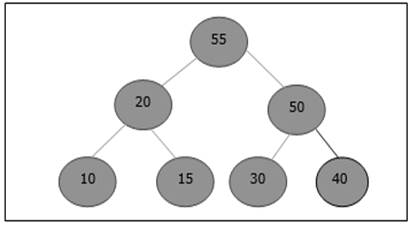
現在，我們必須停止。

示例

以下是此操作在各種程式語言中的實現：

C C++ Java Python

#include <stdio.h>
void swap(int* a, int* b) {
   int temp = *a;
   *a = *b;
   *b = temp;
}
int parent(int i) {
   if (i == 0)
      return -1;
   else
      return (i - 1) / 2;
}
void maxHeapInsert(int arr[], int* heapSize, int key) {
   (*heapSize)++;
   int i = *heapSize;
   arr[i] = key;
   while (i > 1 && arr[parent(i)] < arr[i]) {
      swap(&arr[i], &arr[parent(i)]);
      i = parent(i);
   }
}
int main() {
   int arr[100] = { 50, 30, 40, 20, 15, 10 }; // Initial Max-Heap
   int heapSize = 5; // Current heap size
   // New element to be inserted
   int newElement = 5;
   // Insert the new element into the Max-Heap
   maxHeapInsert(arr, &heapSize, newElement);
   // Print the updated Max-Heap
   printf("Updated Max-Heap: ");
   for (int i = 0; i <= heapSize; i++)
      printf("%d ", arr[i]);
   printf("\n");
   return 0;
}

輸出

Updated Max-Heap: 50 30 40 20 15 10 5

#include <iostream>
#include <vector>
using namespace std;
void swap(int& a, int& b) {
   int temp = a;
   a = b;
   b = temp;
}
int parent(int i) {
   if (i == 0)
      return -1;
   else
      return (i - 1) / 2;
}
void maxHeapInsert(vector<int>& arr, int& heapSize, int key) {
   heapSize++;
   int i = heapSize;   
   // Resize the vector to accommodate the new element
   arr.push_back(0);
   arr[i] = key;
   while (i > 1 && arr[parent(i)] < arr[i]) {
      swap(arr[i], arr[parent(i)]);
      i = parent(i);
   }
}
int main() {
   vector<int> arr = { 50, 30, 40, 20, 15, 10 }; // Initial Max-Heap
   int heapSize = 5; // Current heap size
   // New element to be inserted
   int newElement = 5;
   // Insert the new element into the Max-Heap
   maxHeapInsert(arr, heapSize, newElement);
   // Print the updated Max-Heap
   cout << "Updated Max-Heap: ";
   for (int i = 0; i <= heapSize; i++)
      cout << arr[i] << " ";
   cout << endl;
   return 0;
}

輸出

Updated Max-Heap: 50 30 40 20 15 10 5

import java.util.Arrays;
public class MaxHeap {
   public static void swap(int arr[], int i, int j) {
      int temp = arr[i];
      arr[i] = arr[j];
      arr[j] = temp;
   }
   public static int parent(int i) {
      if (i == 0)
         return -1;
      else
         return (i - 1) / 2;
   }
   public static void maxHeapInsert(int arr[], int heapSize, int key) {
      heapSize++;
      int i = heapSize - 1; // Adjust the index for array insertion
      arr[i] = key;
      while (i > 0 && arr[parent(i)] < arr[i]) {
         swap(arr, i, parent(i));
         i = parent(i);
      }
   }
   public static void main(String args[]) {
      int arr[] = { 50, 30, 40, 20, 15, 10 }; // Initial Max-Heap
      int heapSize = 5; // Current heap size
      // New element to be inserted
      int newElement = 5;
      // Insert the new element into the Max-Heap
      maxHeapInsert(arr, heapSize, newElement);
      // Print the updated Max-Heap
      System.out.print("Updated Max-Heap: ");
      for (int i = 0; i <= heapSize; i++)
         System.out.print(arr[i] + " ");
      System.out.println();
   }
}

輸出

Updated Max-Heap: 50 30 40 20 15 5

def swap(arr, i, j):
    arr[i], arr[j] = arr[j], arr[i]
def parent(i):
    if i == 0:
        return -1
    else:
        return (i - 1) // 2
def max_heap_insert(arr, heap_size, key):
    heap_size += 1
    i = heap_size
    arr.append(key)
    while i > 0 and arr[parent(i)] < arr[i]:
        swap(arr, i, parent(i))
        i = parent(i)
if __name__ == "__main__":
    arr = [50, 30, 40, 20, 15, 10] # Initial Max-Heap
    heap_size = 5 # Current heap size
    # New element to be inserted
    new_element = 5
    # Insert the new element into the Max-Heap
    max_heap_insert(arr, heap_size, new_element)
    # Print the updated Max-Heap
    print("Updated Max-Heap:", arr)

輸出

Updated Max-Heap: [50, 30, 40, 20, 15, 10, 5]

列印頁面