從堆中提取根元素

Table of content
上一頁
下一頁

extract方法用於提取堆的根元素。以下是演算法。

虛擬碼

Heap-Extract-Max (numbers[]) 
max = numbers[1] 
numbers[1] = numbers[heapsize] 
heapsize = heapsize – 1 
Max-Heapify (numbers[], 1) 
return max

示例

讓我們考慮前面討論的相同示例。現在我們要提取一個元素。此方法將返回堆的根元素。

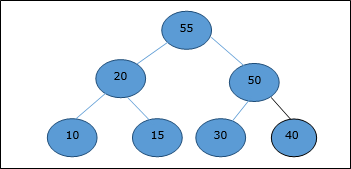
Method

刪除根元素後，最後一個元素將移動到根位置。

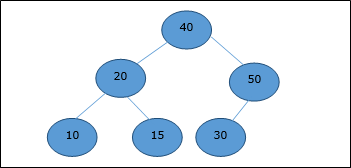
Root Element

現在，將呼叫Heapify函式。Heapify之後，將生成以下堆。

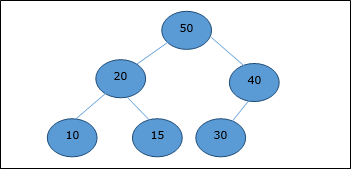
Heapify

實現

以下是此操作在各種程式語言中的實現：

C C++ Java Python
#include <stdio.h>
void swap(int arr[], int i, int j) {
   int temp = arr[i];
   arr[i] = arr[j];
   arr[j] = temp;
}
void maxHeapify(int arr[], int size, int i) {
   int leftChild = 2 * i + 1;
   int rightChild = 2 * i + 2;
   int largest = i;
   if (leftChild < size && arr[leftChild] > arr[largest])
      largest = leftChild;
   if (rightChild < size && arr[rightChild] > arr[largest])
      largest = rightChild;
   if (largest != i) {
      swap(arr, i, largest);
      maxHeapify(arr, size, largest); // Recursive call to continue heapifying
   }
}
int extractMax(int arr[], int *heapSize) {
   if (*heapSize < 1) {
      printf("Heap underflow!\n");
      return -1;
   }
   int max = arr[0];
   arr[0] = arr[*heapSize - 1];
   (*heapSize)--;
   maxHeapify(arr, *heapSize, 0); // Heapify the updated heap
   return max;
}
int main() {
   int arr[] = { 55, 50, 30, 40, 20, 15, 10 }; // Max-Heap
   int heapSize = sizeof(arr) / sizeof(arr[0]);
   int max = extractMax(arr, &heapSize); // Extract the max element from the heap
   printf("Extracted Max Element: %d\n", max);
   // Print the updated Max-Heap
   printf("Updated Max-Heap: ");
   for (int i = 0; i < heapSize; i++)
       printf("%d ", arr[i]);
   printf("\n");
   return 0;
}

輸出

Extracted Max Element: 55
Updated Max-Heap: 50 40 30 10 20 15 

#include <iostream>
#include <vector>
void swap(std::vector<int>& arr, int i, int j) {
   int temp = arr[i];
   arr[i] = arr[j];
   arr[j] = temp;
}
void maxHeapify(std::vector<int>& arr, int size, int i) {
   int leftChild = 2 * i + 1;
   int rightChild = 2 * i + 2;
   int largest = i;
   if (leftChild < size && arr[leftChild] > arr[largest])
      largest = leftChild;
   
   if (rightChild < size && arr[rightChild] > arr[largest])
      largest = rightChild;
   if (largest != i) {
      swap(arr, i, largest);
      maxHeapify(arr, size, largest); // Recursive call to continue heapifying
   }
}
int extractMax(std::vector<int>& arr, int& heapSize) {
   if (heapSize < 1) {
      std::cout << "Heap underflow!" << std::endl;
      return -1;
   }
   int max = arr[0];
   arr[0] = arr[heapSize - 1];
   heapSize--;
   maxHeapify(arr, heapSize, 0); // Heapify the updated heap
   return max;
}
int main() {
   std::vector<int> arr = { 55, 50, 30, 40, 20, 15, 10 }; // Max-Heap
   int heapSize = arr.size();
   int max = extractMax(arr, heapSize); // Extract the max element from the heap
   std::cout << "Extracted Max Element: " << max << std::endl;
   // Print the updated Max-Heap
   std::cout << "Updated Max-Heap: ";
   for (int i = 0; i < heapSize; i++)
       std::cout << arr[i] << " ";
   std::cout << std::endl;
   return 0;
}

輸出

Extracted Max Element: 55
Updated Max-Heap: 50 40 30 10 20 15 

import java.util.Arrays;
public class MaxHeap {
   public static void swap(int arr[], int i, int j) {
      int temp = arr[i];
      arr[i] = arr[j];
      arr[j] = temp;
   }
   public static void maxHeapify(int arr[], int size, int i) {
      int leftChild = 2 * i + 1;
      int rightChild = 2 * i + 2;
      int largest = i;
      if (leftChild < size && arr[leftChild] > arr[largest])
         largest = leftChild;
      if (rightChild < size && arr[rightChild] > arr[largest])
         largest = rightChild;
      if (largest != i) {
         swap(arr, i, largest);
         maxHeapify(arr, size, largest); // Recursive call to continue heapifying
      }
   }
   public static int extractMax(int arr[], int heapSize) {
      if (heapSize < 1) {
          System.out.println("Heap underflow!");
          return -1;
      }
      int max = arr[0];
      arr[0] = arr[heapSize - 1];
      heapSize--;
      maxHeapify(arr, heapSize, 0); // Heapify the updated heap
      return max;
      }
public static void main(String args[]) {
   int arr[] = { 55, 50, 30, 40, 20, 15, 10 }; // Max-Heap
   int heapSize = arr.length;
   int max = extractMax(arr, heapSize); // Extract the max element from the heap
   System.out.println("Extracted Max Element: " + max);
   // Print the updated Max-Heap
   System.out.print("Updated Max-Heap: ");
   for (int i = 0; i < heapSize; i++)
      System.out.print(arr[i] + " ");
   System.out.println();
   }
}

輸出

Extracted Max Element: 55
Updated Max-Heap: 50 40 30 10 20 15 10 

def swap(arr, i, j):
    arr[i], arr[j] = arr[j], arr[i]
def max_heapify(arr, size, i):
    left_child = 2 * i + 1
    right_child = 2 * i + 2
    largest = i
    if left_child < size and arr[left_child] > arr[largest]:
        largest = left_child
    if right_child < size and arr[right_child] > arr[largest]:
        largest = right_child
    if largest != i:
        swap(arr, i, largest)
        max_heapify(arr, size, largest) # Recursive call to continue heapifying
def extract_max(arr, heap_size):
    if heap_size < 1:
        print("Heap underflow!")
        return -1
    max_element = arr[0]
    arr[0] = arr[heap_size - 1]
    heap_size -= 1
    max_heapify(arr, heap_size, 0) # Heapify the updated heap
    return max_element
arr = [55, 50, 30, 40, 20, 15, 10] # Max-Heap
heap_size = len(arr)
max_element = extract_max(arr, heap_size) # Extract the max element from the heap
print("Extracted Max Element:", max_element)
# Print the updated Max-Heap
print("Updated Max-Heap:", arr)

輸出

Extracted Max Element: 55
Updated Max-Heap: [50, 40, 30, 10, 20, 15, 10]
列印頁面
上一頁
下一頁
廣告