空間複雜度

本章將討論計算問題在演算法所需空間量方面的複雜度。

空間複雜度與時間複雜度有很多共同特徵，並作為根據計算難度對問題進行分類的另一種方法。

什麼是空間複雜度？

空間複雜度是一個函式，它描述了演算法根據演算法的輸入量所佔用的記憶體（空間）量。

我們經常談論的是所需的**額外記憶體**，不包括儲存輸入本身所需的記憶體。同樣，我們使用自然（但固定長度）單位來測量它。

我們可以使用位元組，但更容易使用，例如，使用的整數個數，固定大小結構的個數等。

最終，我們得出的函式將與表示該單位所需的實際位元組數無關。

有時會忽略空間複雜度，因為使用的空間很少和/或很明顯，但是有時它變得和時間複雜度一樣重要。

定義

設**M**為一個在所有輸入上都停止的確定性**圖靈機(TM)**。**M**的空間複雜度是函式$f \colon N \rightarrow N$，其中**f(n)**是**M**掃描任何長度為**M**的輸入時使用的磁帶單元格的最大數量。如果**M**的空間複雜度為**f(n)**，我們可以說**M**在空間**f(n)**內執行。

我們使用漸近符號來估計圖靈機的空間複雜度。

設$f \colon N \rightarrow R^+$為一個函式。空間複雜度類可以定義如下：

SPACE = {L | L是由O(f(n))空間確定性TM決定的語言}

SPACE = {L | L是由O(f(n))空間非確定性TM決定的語言}

**PSPACE**是在確定性圖靈機上可以用多項式空間解決的語言的集合。

換句話說，**PSPACE = U_k SPACE (n^k)**

Savitch定理

與空間複雜度相關的最早定理之一是Savitch定理。根據該定理，確定性機器可以使用少量空間來模擬非確定性機器。

對於時間複雜度，這種模擬似乎需要時間呈指數增長。對於空間複雜度，該定理表明，任何使用**f(n)**空間的非確定性圖靈機都可以轉換為使用**f²(n)**空間的確定性TM。

因此，Savitch定理指出，對於任何函式$f \colon N \rightarrow R^+$，其中$f(n) \geqslant n$

NSPACE(f(n)) ⊆ SPACE(f(n))

複雜度類之間的關係

下圖描述了不同複雜度類之間的關係。

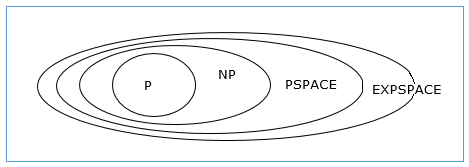
到目前為止，我們還沒有在本教程中討論P類和NP類。這些將在稍後討論。