二叉堆的設計與分析

堆有很多種型別，但在本章中，我們將討論二叉堆。二叉堆是一種資料結構，它看起來類似於一棵完全二叉樹。堆資料結構遵循下面討論的排序屬性。通常，堆用陣列表示。在本章中，我們用H表示堆。

由於堆的元素儲存在陣列中，假設起始索引為1，則第i個元素的父節點的位置可以在⌊ i/2 ⌋找到。第i個節點的左孩子和右孩子分別位於2i和2i + 1的位置。

根據排序屬性，二叉堆可以進一步分類為最大堆或最小堆。

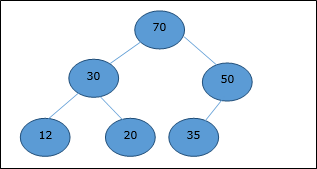
最大堆

在這種堆中，節點的鍵值大於或等於其最高子節點的鍵值。

因此，H[Parent(i)] ≥ H[i]

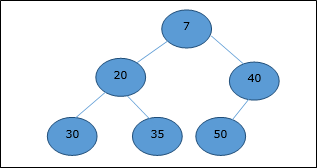
最小堆

在最小堆中，節點的鍵值小於或等於其最低子節點的鍵值。

因此，H[Parent(i)] ≤ H[i]

在本例中，基本操作如下所示，針對最大堆。在堆中插入和刪除元素需要重新排列元素。因此，需要呼叫堆化函式。

陣列表示

完全二叉樹可以用陣列表示，使用層序遍歷儲存其元素。

讓我們考慮一個堆（如下所示），它將由陣列H表示。

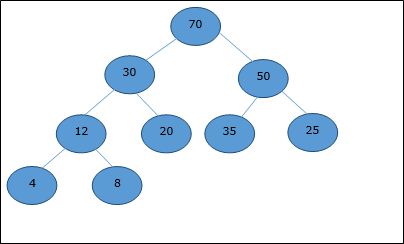
假設起始索引為0，使用層序遍歷，元素按如下方式儲存在陣列中。

在本例中，堆上的操作針對最大堆進行表示。

要查詢索引為i的元素的父節點的索引，使用以下演算法Parent (numbers[], i)。

Algorithm: Parent (numbers[], i) 
if i == 1 
   return NULL 
else 
   [i / 2]

可以使用以下演算法Left-Child (numbers[], i)查詢索引為i的元素的左孩子的索引。

Algorithm: Left-Child (numbers[], i) 
If 2 * i ≤ heapsize 
   return [2 * i] 
else 
   return NULL 

可以使用以下演算法Right-Child(numbers[], i)查詢索引為i的元素的右孩子的索引。

Algorithm: Right-Child (numbers[], i) 
if 2 * i < heapsize 
   return [2 * i + 1] 
else 
   return NULL