作圖：已知$BC = 7.5\ cm$，$AC = 5\ cm$，$\angle C = 60^{\circ}$，構造三角形$∆ABC$。
待辦事項：構造三角形$∆ABC$，其中$BC = 7.5\ cm$，$AC = 5\ cm$，$m \angle C = 60^{\circ}$。
作圖步驟
- 讓我們畫一條線段$BC$，長度為$7.5\ cm$。
- 從點$C$出發，畫一條射線$CX$，使它與$BC$的夾角為$60^{\circ}$，即$\angle ACB=60^{\circ}$。
- 以$C$為圓心，畫一個半徑為$5\ cm$的圓弧，該圓弧與$CX$相交於點$A$。
- 現在，連線$AB$，得到所需的三角形。
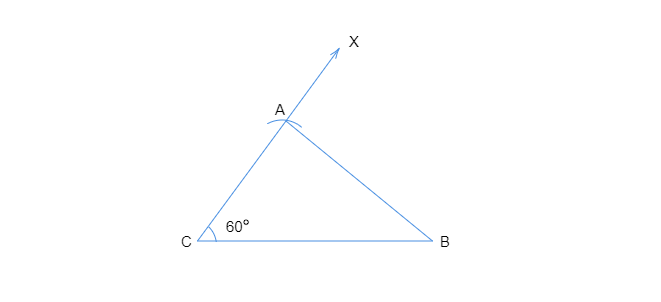
$\triangle ABC$ 是所求的三角形。
因此，構造完成！
- 相關文章
- 作圖：在$∆ABC$中，$BC = 3.6\ cm, AB + AC = 4.8\ cm$，且$\angle B = 60^o$。
- 僅使用直尺和圓規，作圖：已知$∆ABC$，底邊$BC = 7\ cm, \angle ABC = 60^o$，且$AB + AC = 12\ cm$。
- 作圖：構造$∆ABC$，使得$AB=2.5\ cm$，$BC=6\ cm$，$AC=6.5\ cm$。測量$\angle B$。
- 作圖：構造$∆ABC$，已知$m\angle A = 60^{\circ}$，$m\angle B = 30^{\circ}$，且$AB = 5.8\ cm$。
- 作圖：構造$∆ABC$，其中$AB + AC = 5.6\ cm, BC = 4.5\ cm$，且$\angle B = 45^o$。
- ∆ABC ~ ∆LMN。在∆ABC中，AB = 5.5 cm，BC = 6 cm，CA = 4.5 cm。構造∆ABC和∆LMN，使得$\frac{BC}{MN} \ =\ \frac{5}{4}$。
- 作圖：構造$∆DEF$，使得$DE = 5\ cm$，$DF = 3\ cm$，且$\angle EDF = 90^{\circ}$。
- 作圖：構造$\vartriangle ABC$，其中$BC=7\ cm,\ \angle B=75^{o}$，且$AB+AC=12\ cm$。
- 作圖：構造$\triangle ABC$，其中$BC = 3.4\ cm, AB - AC = 1.5\ cm$，且$\angle B = 45^o$。
- 作圖：構造一個三角形\( \mathrm{ABC} \)，其中\( \mathrm{BC}=7 \mathrm{~cm}, \angle \mathrm{B}=75^{\circ} \)，且\( \mathrm{AB}+\mathrm{AC}=13 \mathrm{~cm} \)。
- 作圖：構造一個三角形\( \mathrm{ABC} \)，其中\( \mathrm{BC}=8 \mathrm{~cm}, \angle \mathrm{B}=45^{\circ} \)，且\( \mathrm{AB}-\mathrm{AC}=3.5 \mathrm{~cm} \)。
- 作圖：構造一個等腰直角三角形$ABC$，其中$m\angle ACB = 90^{\circ}$，且$AC = 6\ cm$。
- 選擇正確的答案並說明理由：在$∆ABC$中，$AB = 6\sqrt3\ cm, AC = 12\ cm$，且$BC = 6\ cm$。角B為：（a）$120^o$（b）$60^o$（c）$90^o$（d）$45^o$
- 作圖：如果$PQ = 5\ cm$，$m\angle\ PQR = 105^{\circ}$，且$m\angle QRP = 40^{\circ}$，則構造$∆PQR$。[提示：回顧三角形內角和性質。]
- 作圖：構造一個與\( \triangle A B C \)相似的三角形，其中\( A B=4.6 \mathrm{~cm}, \mathrm{BC}=5.1 \mathrm{~cm}, \angle A=60^{\circ} \)，比例因子為\( 4: 5 \)。
資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究