計算機圖形學 - 直線生成演算法

一條直線連線兩點。它是圖形的基本元素。要繪製一條直線，需要兩點，在這兩點之間可以繪製直線。在以下三種演算法中，我們將直線的一點表示為$X_{0}, Y_{0}$，直線的另一點表示為$X_{1}, Y_{1}$。

DDA演算法

數字微分分析儀 (DDA) 演算法是一種簡單的直線生成演算法，這裡將逐步解釋。

步驟 1 − 獲取兩端點的輸入 $(X_{0}, Y_{0})$ 和 $(X_{1}, Y_{1})$。

步驟 2 − 計算兩端點之間的差值。

dx = X₁ - X₀
dy = Y₁ - Y₀

步驟 3 − 基於步驟 2 中計算出的差值，需要確定放置畫素的步數。如果 dx > dy，則需要在 x 座標上增加更多步數；否則在 y 座標上增加更多步數。

if (absolute(dx) > absolute(dy))
   Steps = absolute(dx);
else
   Steps = absolute(dy);

步驟 4 − 計算 x 座標和 y 座標的增量。

Xincrement = dx / (float) steps;
Yincrement = dy / (float) steps;

步驟 5 − 透過連續遞增 x 和 y 座標來放置畫素，完成直線的繪製。

for(int v=0; v < Steps; v++)
{
   x = x + Xincrement;
   y = y + Yincrement;
   putpixel(Round(x), Round(y));
}

Bresenham 直線生成演算法

Bresenham 演算法是另一種增量掃描轉換演算法。該演算法的一大優點是它只使用整數計算。沿 x 軸以單位間隔移動，並在每一步選擇兩個不同的 y 座標之間的一個。

例如，如下所示，從位置 (2, 3) 需要在 (3, 3) 和 (3, 4) 之間選擇。您希望選擇更靠近原始直線的點。

在取樣位置 $X_{k}+1$，從數學直線到垂直方向的距離分別標記為 $d_{upper}$ 和 $d_{lower}$。

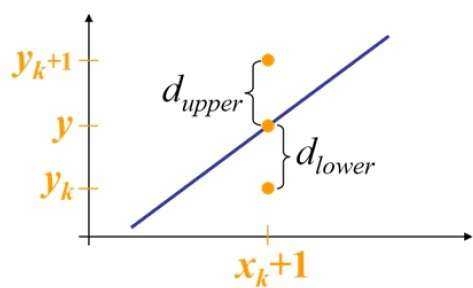
從上圖可以看出，在 $x_{k}+1$ 處數學直線上的 y 座標為：

Y = m($X_{k}$+1) + b

因此，$d_{upper}$ 和 $d_{lower}$ 給出如下：

$$d_{lower} = y-y_{k}$$

$$= m(X_{k} + 1) + b - Y_{k}$$

和

$$d_{upper} = (y_{k} + 1) - y$$

$= Y_{k} + 1 - m (X_{k} + 1) - b$

您可以使用這些來做出關於哪個畫素更靠近數學直線的簡單決定。這個簡單的決定是基於兩個畫素位置之間的差異。

$$d_{lower} - d_{upper} = 2m(x_{k} + 1) - 2y_{k} + 2b - 1$$

讓我們用 dy/dx 代替 m，其中 dx 和 dy 是端點之間的差值。

$$dx (d_{lower} - d_{upper}) =dx(2\frac{\mathrm{d} y}{\mathrm{d} x}(x_{k} + 1) - 2y_{k} + 2b - 1)$$

$$ = 2dy.x_{k} - 2dx.y_{k} + 2dy + 2dx(2b-1)$$

$$ = 2dy.x_{k} - 2dx.y_{k} + C$$

因此，沿直線的第 k 步的決策引數 $P_{k}$ 由下式給出：

$$p_{k} = dx(d_{lower} - d_{upper})$$

$$ = 2dy.x_{k} - 2dx.y_{k} + C$$

決策引數 $P_{k}$ 的符號與 $d_{lower} - d_{upper}$ 的符號相同。

如果 $p_{k}$ 為負，則選擇下畫素，否則選擇上畫素。

請記住，座標變化沿 x 軸以單位步長髮生，因此您可以使用整數計算完成所有操作。在步驟 k+1 處，決策引數給出為：

$$p_{k +1} = 2dy.x_{k + 1} - 2dx.y_{k + 1} + C$$

從中減去 $p_{k}$，我們得到：

$$p_{k + 1} - p_{k} = 2dy(x_{k + 1} - x_{k}) - 2dx(y_{k + 1} - y_{k})$$

但是，$x_{k+1}$ 與 $(xk)+1$ 相同。所以：

$$p_{k+1} = p_{k} + 2dy - 2dx(y_{k+1} - y_{k})$$

其中，$Y_{k+1} – Y_{k}$ 為 0 或 1，具體取決於 $P_{k}$ 的符號。

在 $(x_{0}, y_{0})$ 處計算的第一個決策引數 $p_{0}$ 為：

$$p_{0} = 2dy - dx$$

現在，記住以上所有要點和計算，以下是斜率 m < 1 的 Bresenham 演算法：

步驟 1 − 輸入直線的兩個端點，將左端點儲存在 $(x_{0}, y_{0})$ 中。

步驟 2 − 繪製點 $(x_{0}, y_{0})$。

步驟 3 − 計算常數 dx、dy、2dy 和 (2dy – 2dx)，並獲得決策引數的第一個值：

$$p_{0} = 2dy - dx$$

步驟 4 − 沿直線的每個 $X_{k}$（從 k = 0 開始），執行以下測試：

如果 $p_{k}$ < 0，則下一個要繪製的點是 $(x_{k}+1, y_{k})$，並且

$$p_{k+1} = p_{k} + 2dy$$ 否則，

$$(x_{k}, y_{k}+1)$$

$$p_{k+1} = p_{k} + 2dy - 2dx$$

步驟 5 − 重複步驟 4 (dx – 1) 次。

對於 m > 1，確定每次遞增 y 時是否需要遞增 x。

求解後，決策引數 $P_{k}$ 的方程將非常相似，只是方程中的 x 和 y 會互換。

中點演算法

中點演算法是由 Bresenham 提出的，後來由 Pitteway 和 Van Aken 修改。假設您已經將點 P 放置在 (x, y) 座標上，並且直線的斜率為 0 ≤ k ≤ 1，如下圖所示。

現在需要確定是將下一個點放在 E 還是 N。這可以透過識別最接近點 N 或 E 的交點 Q 來選擇。如果交點 Q 最接近點 N，則 N 被認為是下一個點；否則為 E。

為了確定這一點，首先計算中點 M(x+1, y + ½)。如果直線與連線 E 和 N 的垂直線的交點 Q 在 M 下方，則取 E 為下一個點；否則取 N 為下一個點。

為了檢查這一點，我們需要考慮隱式方程：

F(x,y) = mx + b - y

對於正 m 在任何給定的 X，

如果 y 在直線上，則 F(x, y) = 0
如果 y 在直線上方，則 F(x, y) < 0
如果 y 在直線下方，則 F(x, y) > 0

列印頁面