
計算機圖形學 - 3D 計算機圖形學
在二維繫統中,我們僅使用兩個座標 X 和 Y,但在三維中,會增加一個額外的座標 Z。3D 圖形技術及其應用是娛樂、遊戲和計算機輔助設計行業的基礎。它是科學視覺化領域持續的研究領域。
此外,3D 圖形元件現在已成為幾乎每臺個人電腦的一部分,雖然傳統上它們旨在用於圖形密集型軟體(如遊戲),但它們正越來越多地被其他應用程式使用。
平行投影
平行投影丟棄 z 座標,並擴充套件物件上每個頂點的平行線,直到它們與視平面相交。在平行投影中,我們指定投影方向而不是投影中心。
在平行投影中,投影中心到投影平面的距離是無限的。在這種型別的投影中,我們透過對應於原始物件上連線的線段連線投影頂點。
平行投影不太真實,但它們非常適合精確測量。在這種型別的投影中,平行線保持平行,角度不保留。各種型別的平行投影如下所示。
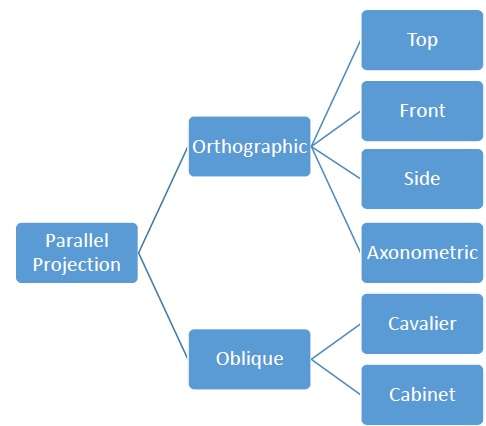
正投影
在正投影中,投影方向垂直於平面的投影。正投影有三種類型:
- 正面投影
- 頂面投影
- 側面投影

斜投影
在斜投影中,投影方向不垂直於平面的投影。在斜投影中,我們可以比正投影更好地觀察物件。
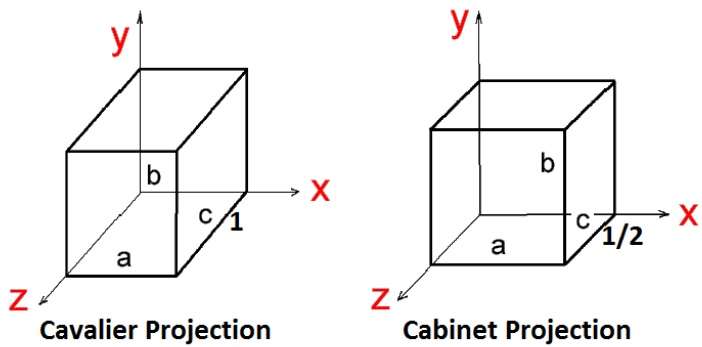
斜投影有兩種型別:**騎士**和**櫥櫃**。騎士投影與投影平面成 45° 角。在騎士投影中,垂直於視平面的線的投影與該線本身具有相同的長度。在騎士投影中,所有三個主要方向的縮短因子相等。
櫥櫃投影與投影平面成 63.4° 角。在櫥櫃投影中,垂直於觀察面的線以其實際長度的一半投影。這兩種投影如下圖所示:
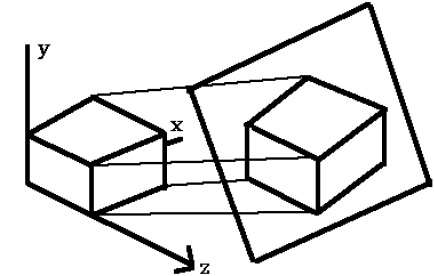
等軸測投影
顯示物件多於一側的正投影稱為**軸測正投影**。最常見的軸測投影是**等軸測投影**,其中投影平面在模型座標系中與每個座標軸相交於相等距離。在這種投影中,線的平行性得以保留,但角度未保留。下圖顯示了等軸測投影:
透視投影
在透視投影中,投影中心到投影平面的距離是有限的,並且物件的大小與距離成反比,這看起來更逼真。
距離和角度不保留,平行線不保持平行。相反,它們全部匯聚到一個點,稱為**投影中心**或**投影參考點**。透視投影有三種類型,如下表所示。
**一點**透視投影很容易繪製。
**兩點**透視投影可以更好地體現深度。
**三點**透視投影是最難繪製的。
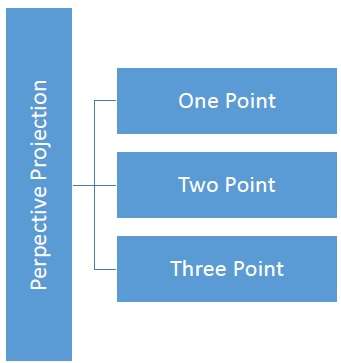
下圖顯示了這三種類型的透視投影:

平移
在 3D 平移中,我們除了 X 和 Y 座標外,還傳遞 Z 座標。3D 平移的過程類似於 2D 平移。平移將物件移動到螢幕上的不同位置。
下圖顯示了平移的效果:
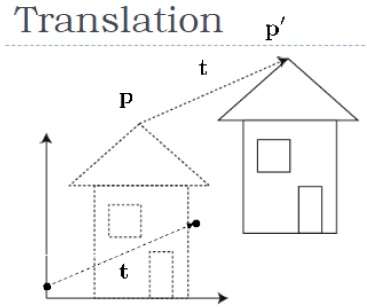
可以透過將平移座標 $(t_{x,} t_{y,} t_{z})$ 新增到原始座標 (X, Y, Z) 以獲得新座標 (X', Y', Z') 來在 3D 中平移一個點。
$T = \begin{bmatrix} 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ t_{x}& t_{y}& t_{z}& 1\\ \end{bmatrix}$
P’ = P∙T
$[X′ \:\: Y′ \:\: Z′ \:\: 1] \: = \: [X \:\: Y \:\: Z \:\: 1] \: \begin{bmatrix} 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ t_{x}& t_{y}& t_{z}& 1\\ \end{bmatrix}$
$= [X + t_{x} \:\:\: Y + t_{y} \:\:\: Z + t_{z} \:\:\: 1]$