計算機圖形學 - 二維變換

變換意味著透過應用規則將某些圖形更改為其他內容。我們可以進行各種型別的變換，例如平移、縮放（放大或縮小）、旋轉、剪下等。當變換髮生在二維平面上時，稱為二維變換。

變換在計算機圖形學中起著重要作用，用於重新定位螢幕上的圖形並更改其大小或方向。

齊次座標

為了執行一系列變換，例如先平移後旋轉再縮放，我們需要遵循一個順序過程：

平移座標；
旋轉平移後的座標；然後
縮放旋轉後的座標以完成複合變換。

為了縮短此過程，我們必須使用3×3變換矩陣而不是2×2變換矩陣。為了將2×2矩陣轉換為3×3矩陣，我們必須新增一個額外的虛擬座標W。

透過這種方式，我們可以用3個數而不是2個數來表示點，這稱為齊次座標系統。在這個系統中，我們可以用矩陣乘法表示所有變換方程。任何笛卡爾點P(X, Y)都可以透過P’ (X_h, Y_h, h)轉換為齊次座標。

平移

平移將物件移動到螢幕上的不同位置。可以透過將平移座標 (t_x, t_y) 新增到原始座標 (X, Y) 來平移二維點，從而得到新的座標 (X’, Y’)。

從上圖可以看出：

X’ = X + t_x

Y’ = Y + t_y

對 (t_x, t_y) 稱為平移向量或位移向量。上述方程也可以用列向量表示。

$P = \begin{bmatrix}X\\Y\end{bmatrix}$ p' = $\begin{bmatrix}X'\\Y'\end{bmatrix}$T = $\begin{bmatrix}t_{x}\\t_{y}\end{bmatrix}$

我們可以寫成：

P’ = P + T

旋轉

在旋轉中，我們圍繞其原點以特定角度 θ（theta）旋轉物件。從下圖可以看出，點 P(X, Y) 位於距原點距離為 r 的水平 X 座標的角度 φ 處。

假設您想將其旋轉角度 θ。旋轉到新的位置後，您將得到一個新的點 P’ (X’, Y’)。

使用標準三角函式，點 P(X, Y) 的原始座標可以表示為：

$X = r \, cos \, \phi ...... (1)$

$Y = r \, sin \, \phi ...... (2)$

同樣，我們可以表示點 P’ (X’, Y’) 為：

${x}'= r \: cos \: \left ( \phi \: + \: \theta \right ) = r\: cos \: \phi \: cos \: \theta \: − \: r \: sin \: \phi \: sin \: \theta ....... (3)$

${y}'= r \: sin \: \left ( \phi \: + \: \theta \right ) = r\: cos \: \phi \: sin \: \theta \: + \: r \: sin \: \phi \: cos \: \theta ....... (4)$

將公式 (1) 和 (2) 分別代入 (3) 和 (4)，我們將得到

${x}'= x \: cos \: \theta − \: y \: sin \: \theta $

${y}'= x \: sin \: \theta + \: y \: cos \: \theta $

將上述方程表示為矩陣形式：

$$[X' Y'] = [X Y] \begin{bmatrix} cos\theta & sin\theta \\ -sin\theta & cos\theta \end{bmatrix}OR $$

P’ = P . R

其中 R 是旋轉矩陣

$$R = \begin{bmatrix} cos\theta & sin\theta \\ -sin\theta & cos\theta \end{bmatrix}$$

旋轉角度可以為正也可以為負。

對於正旋轉角度，我們可以使用上述旋轉矩陣。但是，對於負角度旋轉，矩陣將如下所示更改：

$$R = \begin{bmatrix} cos(-\theta) & sin(-\theta) \\ -sin(-\theta) & cos(-\theta) \end{bmatrix}$$

$$=\begin{bmatrix} cos\theta & -sin\theta \\ sin\theta & cos\theta \end{bmatrix} \left (\because cos(-\theta ) = cos \theta \; and\; sin(-\theta ) = -sin \theta \right )$$

縮放

要更改物件的大小，可以使用縮放變換。在縮放過程中，您可以擴充套件或壓縮物件的大小。可以透過將物件的原始座標與縮放因子相乘來實現縮放，以獲得所需的結果。

讓我們假設原始座標為 (X, Y)，縮放因子為 (S_X, S_Y)，產生的座標為 (X’, Y’)。這可以用下面的數學公式表示：

X' = X . S_X 和 Y' = Y . S_Y

縮放因子 S_X、S_Y 分別沿 X 和 Y 方向縮放物件。上述方程也可以表示為以下矩陣形式：

$$ \begin{bmatrix} X' \\ Y' \end{bmatrix} = \begin{bmatrix} X \\ Y \end{bmatrix} \begin{bmatrix} S_{x} & 0 \\ 0 & S_{y} \end{bmatrix} $$

或

P’ = P . S

其中 S 是縮放矩陣。縮放過程如下圖所示。

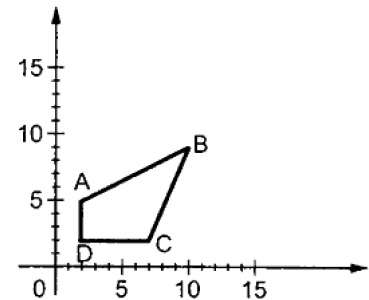
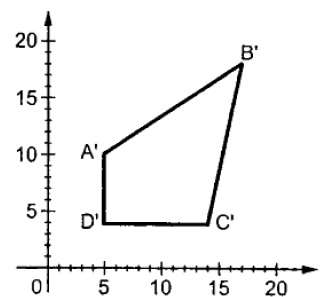
如果我們將小於 1 的值提供給縮放因子 S，則可以減小物件的大小。如果我們提供大於 1 的值，則可以增加物件的大小。

反射

反射是原始物件的映象。換句話說，我們可以說它是 180° 的旋轉操作。在反射變換中，物件的大小不會改變。

下圖分別顯示了關於 X 軸和 Y 軸以及關於原點的反射。

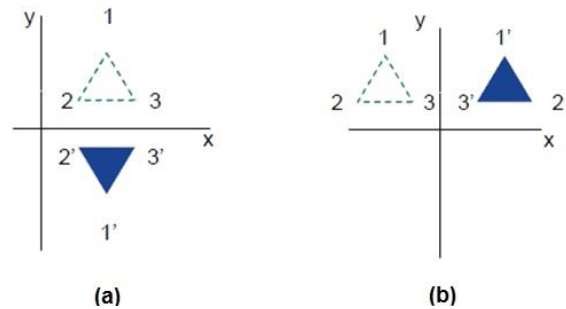
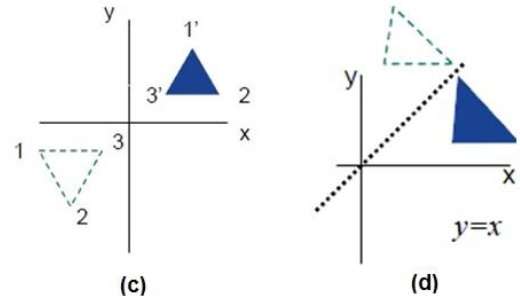
剪下

使物件形狀傾斜的變換稱為剪下變換。有兩種剪下變換：X 剪下和Y 剪下。一種會移動 X 座標值，另一種會移動 Y 座標值。但是，在這兩種情況下，只有一個座標會改變其座標，而另一個座標會保留其值。剪下也稱為傾斜。

X 剪下

X 剪下保留 Y 座標，並對 X 座標進行更改，這會導致垂直線向左或向右傾斜，如下圖所示。

X 剪下的變換矩陣可以表示為：

$$X_{sh} = \begin{bmatrix} 1& shx & 0\\ 0& 1 & 0\\ 0& 0 & 1 \end{bmatrix}$$

Y' = Y + Sh_y . X

X’ = X

Y 剪下

Y 剪下保留 X 座標並更改 Y 座標，這會導致水平線轉換為向上或向下傾斜的線，如下圖所示。

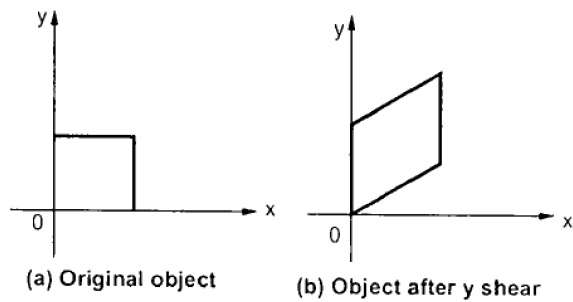
Y 剪下可以用矩陣表示為：

$$Y_{sh} \begin{bmatrix} 1& 0 & 0\\ shy& 1 & 0\\ 0& 0 & 1 \end{bmatrix}$$

X’ = X + Sh_x . Y

Y’ = Y

複合變換

如果平面 T1 的變換後接著是第二個平面變換 T2，則結果本身可以用單個變換 T 來表示，該變換是按該順序組合 T1 和 T2 的結果。這寫成 T = T1∙T2。

複合變換可以透過連線變換矩陣來實現，以獲得組合變換矩陣。

組合矩陣：

[T][X] = [X] [T1] [T2] [T3] [T4] …. [Tn]

其中 [Ti] 是任何組合

平移
縮放
剪下
旋轉
反射

變換順序的變化會導致不同的結果，因為通常矩陣乘法不是累積的，即 [A] . [B] ≠ [B] . [A]，以及乘法的順序。組合變換的基本目的是透過將單個組合變換應用於點來提高效率，而不是一個接一個地應用一系列變換。

例如，要圍繞任意點 (X_p, Y_p) 旋轉物件，我們必須執行三個步驟：

將點 (X_p, Y_p) 平移到原點。
圍繞原點旋轉它。
最後，將旋轉中心移回它所屬的位置。

列印頁面