計算機圖形學 - 快速指南

計算機圖形學 - 基礎

計算機圖形學是用程式設計在電腦螢幕上繪畫的藝術。它涉及資料的計算、建立和處理。換句話說，我們可以說計算機圖形學是用於影像生成和處理的渲染工具。

陰極射線管

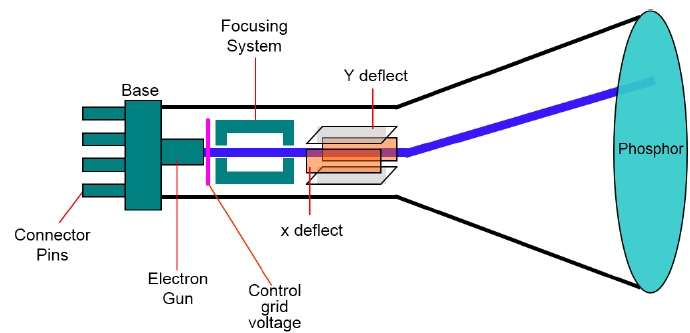
圖形系統中的主要輸出裝置是影片監視器。影片監視器的主要元件是陰極射線管 (CRT)，如下圖所示。

CRT 的工作原理很簡單：

電子槍發射電子束（陰極射線）。
電子束穿過聚焦和偏轉系統，將其引導到磷光塗層螢幕上的指定位置。
當電子束撞擊螢幕時，磷光體在電子束接觸的每個位置發出一個小光點。
它透過快速將電子束重新導回相同的螢幕點來重繪影像。

我們可以透過兩種方式（隨機掃描和光柵掃描）在螢幕上顯示物體。

光柵掃描

在光柵掃描系統中，電子束逐行從上到下掃描螢幕。當電子束移動到每一行時，光束強度會開啟和關閉以建立發光點的圖案。

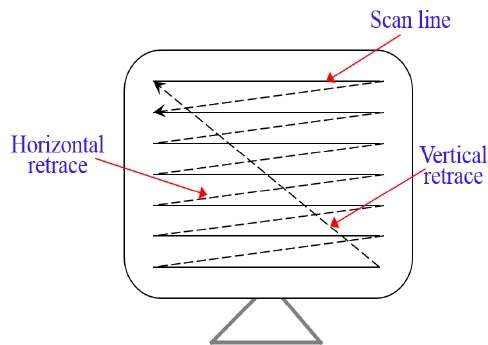
影像定義儲存在稱為重新整理緩衝區或幀緩衝區的記憶體區域中。該記憶體區域儲存所有螢幕點的強度值集。然後從重新整理緩衝區檢索儲存的強度值，並逐行（掃描線）“繪製”到螢幕上，如下圖所示。

每個螢幕點被稱為畫素 (picture element) 或pel。在每條掃描線結束時，電子束返回到螢幕的左側以開始顯示下一條掃描線。

隨機掃描（向量掃描）

在這種技術中，電子束僅指向螢幕上要繪製圖像的部分，而不是像光柵掃描那樣從左到右、從上到下掃描。它也稱為向量顯示、筆劃寫入顯示或書法顯示。

影像定義儲存為一組線描命令，位於稱為重新整理顯示檔案的記憶體區域中。要顯示指定的影像，系統會迴圈遍歷顯示檔案中的命令集，依次繪製每個元件線。處理完所有線描命令後，系統會迴圈回到列表中的第一條線命令。

隨機掃描顯示器設計為每秒繪製圖像的所有元件線 30 到 60 次。

計算機圖形學的應用

計算機圖形學有許多應用，其中一些列在下面：

計算機圖形使用者介面 (GUI) - 一種圖形化的、面向滑鼠的範例，允許使用者與計算機互動。
商務演示圖形 - “一圖勝千言”。
地圖繪製 - 繪製地圖。
天氣圖 - 即時地圖繪製，符號表示。
衛星成像 - 地球影像。
照片增強 - 銳化模糊照片。
醫學成像 - MRI、CAT 掃描等 - 非侵入性內部檢查。
工程圖紙 - 機械、電氣、土木等 - 取代過去的藍圖。
排版 - 在出版物中使用字元影像 - 取代過去的鉛字。
建築 - 施工圖紙、外觀草圖 - 取代過去的藍圖和手繪圖。
藝術 - 計算機為藝術家提供了一種新的媒介。
培訓 - 飛行模擬器、計算機輔助教學等。
娛樂 - 電影和遊戲。
模擬和建模 - 取代物理建模和模擬

直線生成演算法

一條線連線兩點。它是圖形中的基本元素。要繪製一條線，您需要兩點，您可以在這兩點之間繪製一條線。在以下三種演算法中，我們將線的其中一點表示為$X_{0}, Y_{0}$，線的另一點表示為$X_{1}, Y_{1}$。

DDA 演算法

數字微分分析儀 (DDA) 演算法是一種簡單的直線生成演算法，這裡將逐步解釋。

步驟 1 - 獲取兩端點的輸入 $(X_{0}, Y_{0})$ 和 $(X_{1}, Y_{1})$。

步驟 2 - 計算兩端點之間的差值。

dx = X₁ - X₀
dy = Y₁ - Y₀

步驟 3 - 基於步驟 2 中計算出的差值，您需要確定放置畫素的步數。如果 dx > dy，則需要在 x 座標上增加更多步數；否則在 y 座標上增加更多步數。

if (absolute(dx) > absolute(dy))
   Steps = absolute(dx);
else
   Steps = absolute(dy);

步驟 4 - 計算 x 座標和 y 座標的增量。

Xincrement = dx / (float) steps;
Yincrement = dy / (float) steps;

步驟 5 - 透過連續遞增 x 和 y 座標來放置畫素，並完成直線的繪製。

for(int v=0; v < Steps; v++)
{
   x = x + Xincrement;
   y = y + Yincrement;
   putpixel(Round(x), Round(y));
}

Bresenham 直線生成演算法

Bresenham 演算法是另一種增量掃描轉換演算法。該演算法的一大優點是它只使用整數計算。沿 x 軸以單位間隔移動，並在每一步中選擇兩個不同的 y 座標。

例如，如下圖所示，從位置 (2, 3) 您需要在 (3, 3) 和 (3, 4) 之間進行選擇。您希望選擇更靠近原始直線的點。

在樣本位置 $X_{k}+1$，與數學直線的垂直距離標記為 $d_{upper}$ 和 $d_{lower}$。

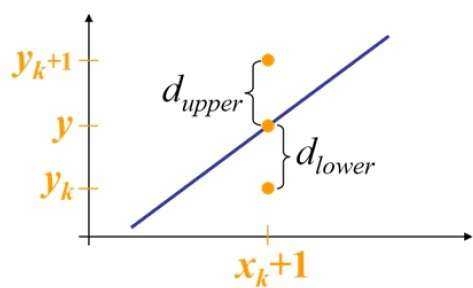
從上圖中，數學直線上 $x_{k}+1$ 處的 y 座標為：

Y = m($X_{k}$+1) + b

所以，$d_{upper}$ 和 $d_{lower}$ 給出如下：

$$d_{lower} = y-y_{k}$$

$$= m(X_{k} + 1) + b - Y_{k}$$

和

$$d_{upper} = (y_{k} + 1) - y$$

$= Y_{k} + 1 - m (X_{k} + 1) - b$

您可以使用這些資訊來做出關於哪個畫素更靠近數學直線的簡單決策。這個簡單的決策是基於兩個畫素位置之間的差異。

$$d_{lower} - d_{upper} = 2m(x_{k} + 1) - 2y_{k} + 2b - 1$$

讓我們用 dy/dx 代替 m，其中 dx 和 dy 是端點之間的差值。

$$dx (d_{lower} - d_{upper}) =dx(2\frac{\mathrm{d} y}{\mathrm{d} x}(x_{k} + 1) - 2y_{k} + 2b - 1)$$

$$ = 2dy.x_{k} - 2dx.y_{k} + 2dy + 2dx(2b-1)$$

$$ = 2dy.x_{k} - 2dx.y_{k} + C$$

所以，直線上第 k 步的決策引數 $P_{k}$ 由下式給出：

$$p_{k} = dx(d_{lower} - d_{upper})$$

$$ = 2dy.x_{k} - 2dx.y_{k} + C$$

決策引數 $P_{k}$ 的符號與 $d_{lower} - d_{upper}$ 的符號相同。

如果 $p_{k}$ 為負，則選擇下畫素，否則選擇上畫素。

記住，座標變化沿 x 軸以單位步長髮生，因此您可以使用整數計算完成所有操作。在步驟 k+1 處，決策引數給出如下：

$$p_{k +1} = 2dy.x_{k + 1} - 2dx.y_{k + 1} + C$$

從中減去 $p_{k}$，我們得到：

$$p_{k + 1} - p_{k} = 2dy(x_{k + 1} - x_{k}) - 2dx(y_{k + 1} - y_{k})$$

但是，$x_{k+1}$ 與 $x_{k+1}$ 相同。所以：

$$p_{k+1} = p_{k} + 2dy - 2dx(y_{k+1} - y_{k})$$

其中，$Y_{k+1} – Y_{k}$ 為 0 或 1，取決於 $P_{k}$ 的符號。

在 $(x_{0}, y_{0})$ 處計算的第一個決策引數 $p_{0}$ 給出如下：

$$p_{0} = 2dy - dx$$

現在，記住以上所有要點和計算，以下是斜率 m < 1 的 Bresenham 演算法：

步驟 1 - 輸入直線的兩個端點，將左端點儲存在 $(x_{0}, y_{0})$ 中。

步驟 2 - 繪製點 $(x_{0}, y_{0})$。

步驟 3 - 計算常數 dx、dy、2dy 和 (2dy – 2dx)，並獲得決策引數的第一個值：

$$p_{0} = 2dy - dx$$

步驟 4 - 沿著直線的每個 $X_{k}$（從 k = 0 開始），執行以下測試：

如果 $p_{k}$ < 0，則下一個要繪製的點是 $(x_{k}+1, y_{k})$，並且

$$p_{k+1} = p_{k} + 2dy$$ 否則，

$$(x_{k}, y_{k}+1)$$

$$p_{k+1} = p_{k} + 2dy - 2dx$$

步驟 5 - 重複步驟 4 (dx – 1) 次。

對於 m > 1，確定每次遞增 y 時是否需要遞增 x。

求解後，決策引數 $P_{k}$ 的方程非常相似，只是方程中的 x 和 y 會互換。

中點演算法

中點演算法是由 Bresenham 提出的，後來由 Pitteway 和 Van Aken 修改。假設您已經將點 P 放置在 (x, y) 座標處，並且直線的斜率為 0 ≤ k ≤ 1，如下圖所示。

現在您需要決定是否將下一個點放在 E 或 N。這可以透過識別最接近點 N 或 E 的交點 Q 來選擇。如果交點 Q 最接近點 N，則將 N 視為下一個點；否則為 E。

要確定這一點，首先計算中點 M(x+1, y + ½)。如果直線與連線 E 和 N 的垂直線的交點 Q 在 M 以下，則取 E 為下一個點；否則取 N 為下一個點。

為了檢查這一點，我們需要考慮隱式方程：

F(x,y) = mx + b - y

對於正 m，在任何給定的 X 處，

如果 y 在直線上，則 F(x, y) = 0
如果 y 在直線上方，則 F(x, y) < 0
如果 y 在直線下方，則 F(x, y) > 0

圓生成演算法

在螢幕上繪製圓圈比繪製直線複雜一些。有兩種流行的圓生成演算法：Bresenham 演算法和中點圓演算法。這些演算法基於確定繪製圓所需後續點的思想。讓我們詳細討論這些演算法：

圓的方程為 $X^{2} + Y^{2} = r^{2}$，其中 r 為半徑。

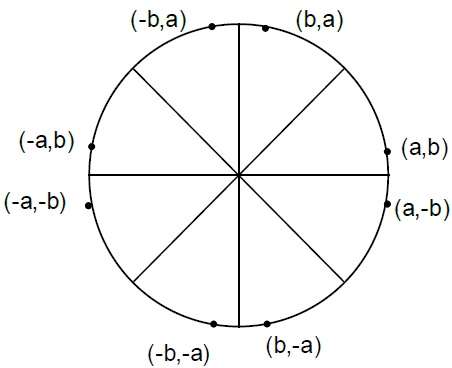
Bresenham 演算法

我們無法在光柵顯示器上顯示連續的弧線。相反，我們必須選擇最接近的畫素位置來完成弧線。

從下圖可以看出，我們已將畫素放在 (X, Y) 位置，現在需要決定將下一個畫素放在哪裡：N (X+1, Y) 或 S (X+1, Y-1)。

這可以透過決策引數 d 來決定。

如果 d <= 0，則選擇 N(X+1, Y) 作為下一個畫素。
如果 d > 0，則選擇 S(X+1, Y-1) 作為下一個畫素。

演算法

步驟 1 - 獲取圓心座標和半徑，並分別將其儲存在 x、y 和 R 中。設定 P=0 和 Q=R。

步驟 2 - 設定決策引數 D = 3 – 2R。

步驟 3 - 當 P ≤ Q 時，重複步驟 4 到步驟 8。

步驟 4 - 呼叫 Draw Circle (X, Y, P, Q)。

步驟 5 - 增加 P 的值。

步驟 6 - 如果 D < 0，則 D = D + 4P + 6。

步驟 7 - 否則設定 R = R - 1，D = D + 4(P-Q) + 10。

步驟 8 − 呼叫 Draw Circle (X, Y, P, Q) 函式。

Draw Circle Method(X, Y, P, Q).

Call Putpixel (X + P, Y + Q).
Call Putpixel (X - P, Y + Q).
Call Putpixel (X + P, Y - Q).
Call Putpixel (X - P, Y - Q).
Call Putpixel (X + Q, Y + P).
Call Putpixel (X - Q, Y + P).
Call Putpixel (X + Q, Y - P).
Call Putpixel (X - Q, Y - P).

中點演算法

步驟 1 − 輸入半徑 r 和圓心 $(x_{c,} y_{c})$，並得到以原點為中心的圓周上的第一個點，方法為：

(x₀, y₀) = (0, r)

步驟 2 − 計算決策引數的初始值：

$P_{0}$ = 5/4 – r (參見下面的描述以瞭解此公式的簡化方法。)

f(x, y) = x² + y² - r² = 0

f(x_i - 1/2 + e, y_i + 1)
        = (x_i - 1/2 + e)² + (y_i + 1)² - r² 
        = (x_i- 1/2)² + (y_i + 1)² - r² + 2(x_i - 1/2)e + e²
        = f(x_i - 1/2, y_i + 1) + 2(x_i - 1/2)e + e² = 0

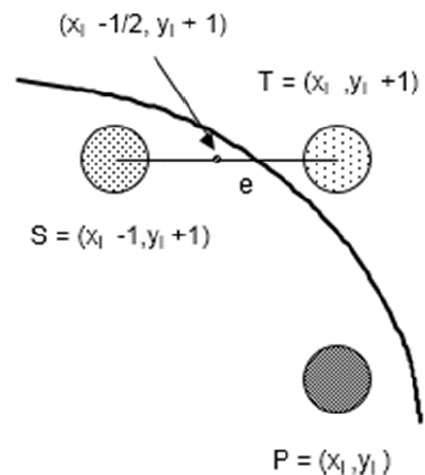
Let d_i = f(x_i - 1/2, y_i + 1) = -2(x_i - 1/2)e - e²
Thus,

If e < 0 then di > 0 so choose point S = (x_i - 1, y_i + 1).
d_i+1    = f(x_i - 1 - 1/2, y_i + 1 + 1) = ((x_i - 1/2) - 1)² + ((y_i + 1) + 1)² - r²
        = d_i - 2(x_i - 1) + 2(y_i + 1) + 1
        = d_i + 2(y_{i + 1} - x_{i + 1}) + 1
		  
If e >= 0 then di <= 0 so choose point T = (x_i, y_i + 1)
   d_i+1 = f(x_i - 1/2, y_i + 1 + 1)
       = d_i + 2y_i+1 + 1
		  
The initial value of di is
   d₀ = f(r - 1/2, 0 + 1) = (r - 1/2)² + 1² - r²
      = 5/4 - r {1-r can be used if r is an integer}
		
When point S = (x_i - 1, y_i + 1) is chosen then
   d_i+1 = d_i + -2x_i+1 + 2y_i+1 + 1
	
When point T = (x_i, y_i + 1) is chosen then
   d_i+1 = d_i + 2y_i+1 + 1

步驟 3 − 從 K=0 開始，在每個 $X_{K}$ 位置執行以下測試：

If P_K < 0 then next point on circle (0,0) is (X_K+1,Y_K) and
   P_K+1 = P_K + 2X_K+1 + 1
Else
   P_K+1 = P_K + 2X_K+1 + 1 – 2Y_K+1
	
Where, 2X_K+1 = 2X_K+2 and 2Y_K+1 = 2Y_K-2.

步驟 4 − 確定其他七個象限的對稱點。

步驟 5 − 將每個計算出的畫素位置 (X, Y) 移動到以 $(X_{C,} Y_{C})$ 為中心的圓周路徑上，並繪製座標值。

X = X + X_C,   Y = Y + Y_C

步驟 6 − 重複步驟 3 到 5，直到 X >= Y。

多邊形填充演算法

多邊形是由一系列頂點組成的有序列表，如下圖所示。為了用特定顏色填充多邊形，需要確定落在多邊形邊界上的畫素以及落在多邊形內部的畫素。本章將介紹如何使用不同的技術填充多邊形。

掃描線演算法

該演算法透過掃描線與多邊形邊的相交來工作，並填充相交點對之間的多邊形。以下步驟描述了該演算法的工作原理。

步驟 1 − 從給定的多邊形中找出 Ymin 和 Ymax。

步驟 2 − 掃描線與多邊形的每條邊從 Ymin 到 Ymax 相交。命名多邊形的每個交點。根據上圖，它們被命名為 p0、p1、p2、p3。

步驟 3 − 按 X 座標的遞增順序排序交點，即 (p0, p1)、(p1, p2) 和 (p2, p3)。

步驟 4 − 填充位於多邊形內部的所有座標對，並忽略交替的座標對。

泛洪填充演算法

有時我們會遇到一個物件，我們希望用不同的顏色填充它的區域及其邊界。我們可以用指定的內部顏色繪製此類物件，而不是像邊界填充演算法那樣搜尋特定的邊界顏色。

它不依賴於物件的邊界，而是依賴於填充顏色。換句話說，它用填充顏色替換物件的內部顏色。當不再存在原始內部顏色的畫素時，演算法完成。

同樣，該演算法依賴於四連通或八連通的畫素填充方法。但它不是尋找邊界顏色，而是尋找所有屬於內部的相鄰畫素。

邊界填充演算法

邊界填充演算法顧名思義。該演算法選擇物件內部的一個點，並開始填充，直到它到達物件的邊界。為了使該演算法工作，邊界顏色和我們填充的顏色應該不同。

在這個演算法中，我們假設整個物件的邊界顏色相同。邊界填充演算法可以透過 4 連通畫素或 8 連通畫素來實現。

4 連通多邊形

在這種技術中，使用 4 連通畫素，如下圖所示。我們在當前畫素的上方、下方、右側和左側放置畫素，這個過程將持續到我們找到具有不同顏色的邊界。

演算法

步驟 1 − 初始化種子點 (seedx, seedy)、填充顏色 fcolor 和預設顏色 dcol 的值。

步驟 2 − 定義多邊形的邊界值。

步驟 3 − 檢查當前種子點是否為預設顏色，如果是，則重複步驟 4 和 5，直到到達邊界畫素。

If getpixel(x, y) = dcol then repeat step 4 and 5

步驟 4 − 將種子點的預設顏色更改為填充顏色。

setPixel(seedx, seedy, fcol)

步驟 5 − 使用四個相鄰點遞迴地執行該過程。

FloodFill (seedx – 1, seedy, fcol, dcol)
FloodFill (seedx + 1, seedy, fcol, dcol)
FloodFill (seedx, seedy - 1, fcol, dcol)
FloodFill (seedx – 1, seedy + 1, fcol, dcol)

步驟 6 − 退出

這種技術存在一個問題。考慮如下所示的情況，我們試圖填充整個區域。這裡，影像只被部分填充。在這種情況下，不能使用 4 連通畫素技術。

8 連通多邊形

在這種技術中，使用 8 連通畫素，如下圖所示。我們像在 4 連通技術中那樣，在當前畫素的上方、下方、右側和左側放置畫素。

除此之外，我們還在對角線上放置畫素，以便覆蓋當前畫素的整個區域。這個過程將持續到我們找到具有不同顏色的邊界。

演算法

步驟 1 − 初始化種子點 (seedx, seedy)、填充顏色 fcolor 和預設顏色 dcol 的值。

步驟 2 − 定義多邊形的邊界值。

步驟 3 − 檢查當前種子點是否為預設顏色，如果是，則重複步驟 4 和 5，直到到達邊界畫素。

If getpixel(x,y) = dcol then repeat step 4 and 5

步驟 4 − 將種子點的預設顏色更改為填充顏色。

setPixel(seedx, seedy, fcol)

步驟 5 − 使用四個相鄰點遞迴地執行該過程。

FloodFill (seedx – 1, seedy, fcol, dcol)
FloodFill (seedx + 1, seedy, fcol, dcol)
FloodFill (seedx, seedy - 1, fcol, dcol)
FloodFill (seedx, seedy + 1, fcol, dcol)
FloodFill (seedx – 1, seedy + 1, fcol, dcol)
FloodFill (seedx + 1, seedy + 1, fcol, dcol)
FloodFill (seedx + 1, seedy - 1, fcol, dcol)
FloodFill (seedx – 1, seedy - 1, fcol, dcol)

步驟 6 − 退出

4 連通畫素技術未能填充下圖中標記的區域，而 8 連通技術則不會出現這種情況。

內外測試

此方法也稱為計數法。在填充物件時，我們經常需要識別特定點是在物件內部還是外部。可以透過兩種方法來識別特定點是在物件內部還是外部。

奇偶規則
非零環繞數規則

奇偶規則

在這種技術中，我們計算從任何點 (x, y) 到無窮大的直線與邊的相交次數。如果交點數為奇數，則點 (x, y) 為內部點。如果交點數為偶數，則點 (x, y) 為外部點。以下是一個示例，以便您更好地理解：

從上圖可以看出，從點 (x, y) 出發，左側的交點數為 5，右側的交點數為 3。因此，總交點數為 8，這是一個奇數。因此，該點被認為在物件內。

非零環繞數規則

此方法也用於簡單多邊形，以測試給定點是否為內部點。可以用大頭針和橡皮筋輕鬆理解。將大頭針固定在多邊形的一條邊上，並將橡皮筋系在上面，然後沿著多邊形的邊拉伸橡皮筋。

當多邊形的所有邊都被橡皮筋覆蓋時，檢查已固定在待測試點上的大頭針。如果我們在該點找到至少一個環繞，則認為該點在多邊形內，否則可以說該點不在多邊形內。

另一種替代方法是，為多邊形的所有邊指定方向。從待測試點畫一條掃描線到 X 方向的最左側。

向上方向的所有邊賦值為 1，其他方向的邊賦值為 -1。
檢查掃描線經過的邊的方向值，並將它們加起來。
如果這些方向值的總和非零，則待測試點為內部點，否則為外部點。
在上圖中，我們將掃描線經過的邊的方向值相加，總和為 1 – 1 + 1 = 1；這是一個非零值。因此，該點被稱為內部點。

觀察與裁剪

裁剪在計算機圖形學中的主要用途是移除位於視區之外的物件、線或線段。視變換對點相對於視景體的位置不敏感——特別是那些位於觀察者後面的點——因此在生成檢視之前必須移除這些點。

點裁剪

從給定視窗中裁剪點非常容易。考慮下圖，其中矩形表示視窗。點裁剪告訴我們給定點 (X, Y) 是否在給定視窗內；並決定我們是否將使用視窗的最小和最大座標。

如果 X 位於 Wx1 ≤ X ≤ Wx2 之間，則給定點的 X 座標在視窗內。同樣，如果 Y 位於 Wy1 ≤ Y ≤ Wy2 之間，則給定點的 Y 座標在視窗內。

線裁剪

線裁剪的概念與點裁剪相同。線上裁剪中，我們將裁剪視窗外部的線段部分，只保留視窗內部的部分。

Cohen-Sutherland 線裁剪演算法

該演算法使用如下圖所示的裁剪視窗。裁剪區域的最小座標為 $(XW_{min,} YW_{min})$，最大座標為 $(XW_{max,} YW_{max})$。

我們將使用 4 位來劃分整個區域。這 4 位分別表示區域的頂部、底部、右側和左側，如下圖所示。這裡，頂部和左側位設定為 1，因為它位於左上角。

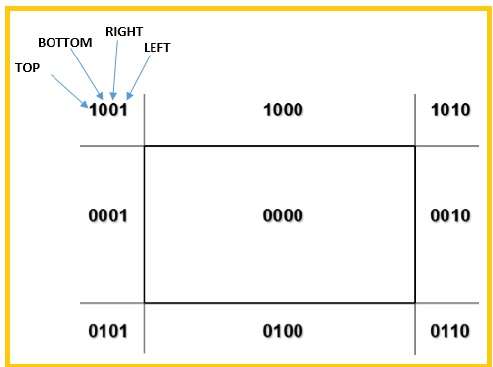
線段有 3 種可能性：

線段可能完全在視窗內（此線段應被接受）。
線段可能完全在視窗外（此線段將完全從區域中移除）。
線段可能部分在視窗內（我們將找到交點，只繪製區域內的線段部分）。

演算法

步驟 1 − 為每個端點分配區域程式碼。

步驟 2 − 如果兩個端點的區域程式碼均為 0000，則接受此線段。

步驟 3 − 否則，對兩個區域程式碼執行邏輯與運算。

步驟 3.1 − 如果結果不是 0000，則拒絕該線段。

步驟 3.2 − 否則需要裁剪。

步驟 3.2.1 − 選擇視窗外的線段端點。

步驟 3.2.2 − 找到視窗邊界上的交點（基於區域程式碼）。

步驟 3.2.3 − 用交點替換端點並更新區域程式碼。

步驟 3.2.4 − 重複步驟 2，直到找到一個被平凡接受或平凡拒絕的裁剪線段。

步驟 4 − 對其他線段重複步驟 1。

Cyrus-Beck 線裁剪演算法

該演算法比 Cohen-Sutherland 演算法更高效。它採用引數線表示和簡單的點積。

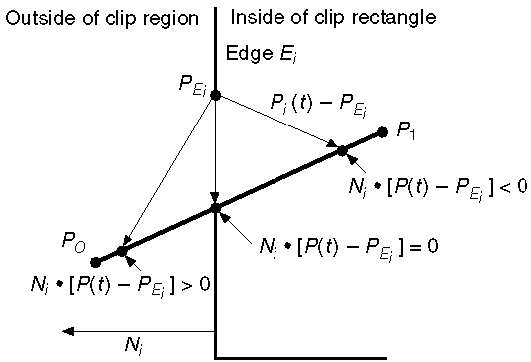
線的引數方程為：

P₀P₁:P(t) = P₀ + t(P₁-P₀)

設 N_i 為外法向量 E_i。現在在邊 E_i 上選擇任意點 P_Ei，則點積 N_i∙[P(t) – P_Ei] 確定點 P(t) 是否“在裁剪邊內”、“在裁剪邊外”或“在裁剪邊上”。

如果 N_i.[P(t) – P_Ei] < 0，則點 P(t) 在內部。

如果 N_i.[P(t) – P_Ei] > 0，則點 P(t) 在外部。

如果 N_i.[P(t) – P_Ei] = 0，則點 P(t) 在邊上（交點）。

N_i∙[P(t) – P_Ei] = 0

N_i∙[ P₀ + t(P₁-P₀) – P_Ei] = 0 (用 P₀ + t(P₁-P₀) 代替 P(t))

N_i∙[P₀ – P_Ei] + N_i∙t[P₁-P₀] = 0

N_i∙[P₀ – P_Ei] + N_i∙tD = 0 (用 D 代替 [P₁-P₀])

N_i∙[P₀ – P_Ei] = - N_i∙tD

t 的方程變為：

$$t = \tfrac{N_{i}.[P_{o} - P_{Ei}]}{{- N_{i}.D}}$$

它對以下條件有效：

N_i ≠ 0（不會發生錯誤）
D ≠ 0 (P₁ ≠ P₀)
N_i∙D ≠ 0 (P₀P₁與E_i不平行)

多邊形裁剪 (Sutherland-Hodgman演算法)

多邊形也可以透過指定裁剪視窗來裁剪。Sutherland-Hodgman多邊形裁剪演算法用於多邊形裁剪。在這個演算法中，多邊形的所有頂點都針對裁剪視窗的每條邊進行裁剪。

首先，多邊形針對多邊形視窗的左邊緣進行裁剪，以獲得多邊形的新頂點。然後使用這些新頂點，針對裁剪視窗的右邊緣、上邊緣和下邊緣裁剪多邊形，如下圖所示。

在處理多邊形邊與裁剪視窗的邊時，如果邊不完全在裁剪視窗內，則找到一個交點，並裁剪從交點到外部邊的部分邊。下圖顯示了左、右、上和下邊緣的裁剪：

文字裁剪

計算機圖形學中使用各種技術來進行文字裁剪。這取決於用於生成字元的方法和特定應用程式的要求。文字裁剪有三種方法，如下所示：

全部或無字串裁剪
全部或無字元裁剪
文字裁剪

下圖顯示了全部或無字串裁剪：

在全部或無字串裁剪方法中，根據裁剪視窗，我們要麼保留整個字串，要麼拒絕整個字串。如上圖所示，STRING2完全在裁剪視窗內，因此我們保留它；STRING1僅部分在視窗內，因此我們拒絕它。

下圖顯示了全部或無字元裁剪：

這種裁剪方法基於字元而不是整個字串。在這種方法中，如果字串完全在裁剪視窗內，則我們保留它。如果它部分在視窗外，則：

只拒絕字串中在視窗外的部分。
如果字元位於裁剪視窗的邊界上，則我們丟棄整個字元並保留其餘字串。

下圖顯示了文字裁剪：

這種裁剪方法基於字元而不是整個字串。在這種方法中，如果字串完全在裁剪視窗內，則我們保留它。如果它部分在視窗外，則：

只拒絕字串中在視窗外的部分。
如果字元位於裁剪視窗的邊界上，則我們只丟棄字元中在裁剪視窗外的部分。

點陣圖圖形

點陣圖是描述影像的畫素集合。它是一種計算機圖形，計算機使用它來儲存和顯示圖片。在這種型別的圖形中，影像逐位儲存，因此被稱為點陣圖圖形。為了更好地理解，讓我們考慮下面的例子，我們使用點陣圖圖形繪製一個笑臉。

現在我們將看到這個笑臉是如何在計算機圖形中逐位儲存的。

仔細觀察原始笑臉，我們可以看到有兩條藍線，在上圖中分別表示為B1、B2和E1、E2。

同樣，笑臉分別由A4、B5、C6、D6、E5和F4的組合位表示。

點陣圖圖形的主要缺點是：

我們無法調整點陣圖影像的大小。如果嘗試調整大小，畫素會變得模糊。
彩色點陣圖可能非常大。

二維變換

變換意味著透過應用規則將某些圖形更改為其他內容。我們可以進行各種型別的變換，例如平移、縮放、旋轉、錯切等。當變換髮生在二維平面上時，稱為二維變換。

變換在計算機圖形學中起著重要的作用，用於重新定位螢幕上的圖形並更改其大小或方向。

齊次座標

為了執行一系列變換，例如先平移後旋轉再縮放，我們需要遵循一個順序過程：

平移座標；
旋轉平移後的座標；然後
縮放旋轉後的座標以完成複合變換。

為了縮短這個過程，我們必須使用3×3變換矩陣而不是2×2變換矩陣。為了將2×2矩陣轉換為3×3矩陣，我們必須新增一個額外的虛擬座標W。

這樣，我們可以用3個數而不是2個數來表示點，這稱為**齊次座標**系統。在這個系統中，我們可以用矩陣乘法表示所有變換方程。任何笛卡爾點P(X, Y)都可以透過P’ (X_h, Y_h, h)轉換為齊次座標。

平移

平移將物件移動到螢幕上的不同位置。可以透過將平移座標(t_x, t_y)新增到原始座標(X, Y)來平移二維點，以獲得新的座標(X’, Y’)。

從上圖中，可以寫出：

X’ = X + t_x

Y’ = Y + t_y

對(t_x, t_y)稱為平移向量或位移向量。上述方程也可以用列向量表示。

$P = \frac{[X]}{[Y]}$ p' = $\frac{[X']}{[Y']}$T = $\frac{[t_{x}]}{[t_{y}]}$

我們可以寫成：

P’ = P + T

旋轉

在旋轉中，我們將物件圍繞其原點旋轉特定角度θ（theta）。從下圖中，我們可以看到點P(X, Y)位於距原點距離為r的水平X座標角度φ處。

假設您想將其旋轉角度θ。旋轉到新的位置後，您將得到一個新的點P’ (X’, Y’)。

使用標準三角函式，點P(X, Y)的原始座標可以表示為：

$X = r \, cos \, \phi ...... (1)$

$Y = r \, sin \, \phi ...... (2)$

同樣，我們可以表示點P’ (X’, Y’)為：

${x}'= r \: cos \: \left ( \phi \: + \: \theta \right ) = r\: cos \: \phi \: cos \: \theta \: − \: r \: sin \: \phi \: sin \: \theta ....... (3)$

${y}'= r \: sin \: \left ( \phi \: + \: \theta \right ) = r\: cos \: \phi \: sin \: \theta \: + \: r \: sin \: \phi \: cos \: \theta ....... (4)$

將公式(1)和(2)分別代入(3)和(4)，我們將得到

${x}'= x \: cos \: \theta − \: y \: sin \: \theta $

${y}'= x \: sin \: \theta + \: y \: cos \: \theta $

將上述方程用矩陣形式表示，

$$[X' Y'] = [X Y] \begin{bmatrix} cos\theta & sin\theta \\ −sin\theta & cos\theta \end{bmatrix}OR $$

P’ = P ∙ R

其中R是旋轉矩陣

$$R = \begin{bmatrix} cos\theta & sin\theta \\ −sin\theta & cos\theta \end{bmatrix}$$

旋轉角度可以是正的也可以是負的。

對於正旋轉角度，我們可以使用上述旋轉矩陣。但是，對於負角度旋轉，矩陣將發生變化，如下所示：

$$R = \begin{bmatrix} cos(−\theta) & sin(−\theta) \\ -sin(−\theta) & cos(−\theta) \end{bmatrix}$$

$$=\begin{bmatrix} cos\theta & −sin\theta \\ sin\theta & cos\theta \end{bmatrix} \left (\because cos(−\theta ) = cos \theta \; and\; sin(−\theta ) = −sin \theta \right )$$

縮放

要更改物件的大小，可以使用縮放變換。在縮放過程中，您會擴充套件或壓縮物件的大小。縮放可以透過將物件的原始座標與縮放因子相乘來實現，以獲得所需的結果。

讓我們假設原始座標是(X, Y)，縮放因子是(S_X, S_Y)，生成的座標是(X’, Y’)。這可以用下面的數學方法表示：

X' = X . S_X 和 Y' = Y . S_Y

縮放因子S_X、S_Y分別沿X和Y方向縮放物件。上述方程也可以用矩陣形式表示如下：

$$\binom{X'}{Y'} = \binom{X}{Y} \begin{bmatrix} S_{x} & 0\\ 0 & S_{y} \end{bmatrix}$$

或

P’ = P . S

其中S是縮放矩陣。縮放過程如下圖所示。

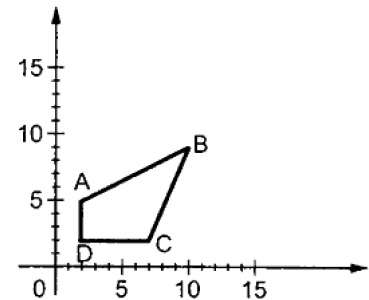
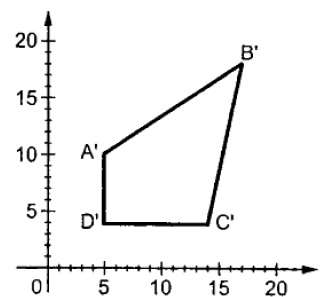
如果我們將小於1的值提供給縮放因子S，那麼我們可以減小物件的大小。如果我們提供大於1的值，那麼我們可以增加物件的大小。

反射

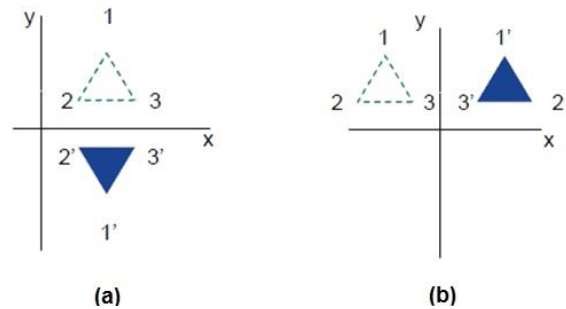
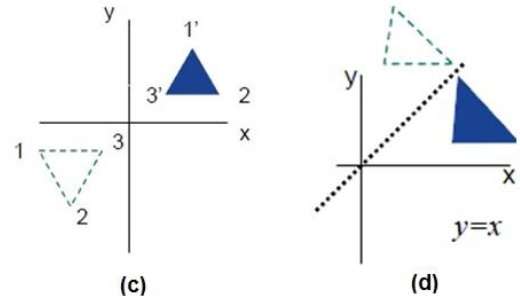
反射是原始物件的映象。換句話說，我們可以說它是一個180°的旋轉操作。在反射變換中，物件的大小不會改變。

下圖分別顯示了關於X軸和Y軸以及關於原點的反射。

錯切

使物體形狀傾斜的變換稱為錯切變換。有兩種錯切變換：**X錯切**和**Y錯切**。一種移動X座標值，另一種移動Y座標值。但是，在這兩種情況下，只有一個座標改變其座標，而另一個保留其值。錯切也稱為**傾斜**。

X錯切

X錯切保留Y座標，並對X座標進行更改，這會導致垂直線向右或向左傾斜，如下圖所示。

X錯切的變換矩陣可以表示為：

$$X_{sh} = \begin{bmatrix} 1& shx & 0\\ 0& 1 & 0\\ 0& 0 & 1 \end{bmatrix}$$

Y' = Y + Sh_y . X

X’ = X

Y錯切

Y錯切保留X座標，並更改Y座標，這會導致水平線變換成向上或向下傾斜的線，如下圖所示。

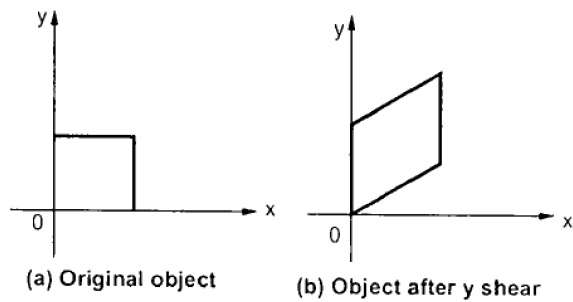
Y錯切可以用矩陣形式表示為：

$$Y_{sh} \begin{bmatrix} 1& 0 & 0\\ shy& 1 & 0\\ 0& 0 & 1 \end{bmatrix}$$

X’ = X + Sh_x . Y

Y’ = Y

複合變換

如果平面變換T1之後是第二個平面變換T2，則結果本身可以用單個變換T表示，它是按該順序取的T1和T2的組合。這寫成T = T1∙T2。

複合變換可以透過連線變換矩陣來實現，以獲得組合變換矩陣。

組合矩陣：

[T][X] = [X] [T1] [T2] [T3] [T4] …. [Tn]

其中[Ti]是任何組合的

平移
縮放
錯切
旋轉
反射

變換順序的改變會導致不同的結果，因為一般矩陣乘法不是可交換的，即[A] . [B] ≠ [B] . [A]，並且乘法的順序。組合變換的基本目的是透過對點應用單個組合變換來提高效率，而不是一個接一個地應用一系列變換。

例如，要圍繞任意點(X_p, Y_p)旋轉一個物件，我們必須執行三個步驟：

將點(X_p, Y_p)平移到原點。
繞原點旋轉。
最後，將旋轉中心移回它原本的位置。

三維計算機圖形學

在二維繫統中，我們只使用 X 和 Y 兩個座標，但在三維繫統中，會增加一個額外的 Z 座標。三維圖形技術及其應用是娛樂、遊戲和計算機輔助設計行業的基礎。它也是科學視覺化領域持續的研究方向。

此外，三維圖形元件現在幾乎成為每臺個人電腦的組成部分，雖然傳統上它們主要用於遊戲等圖形密集型軟體，但它們正越來越多地被其他應用程式使用。

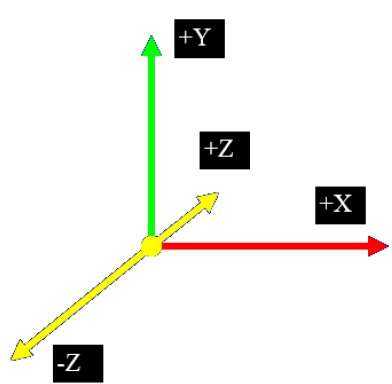
平行投影

平行投影丟棄 z 座標，並將物體上每個頂點的平行線延伸，直到它們與視平面相交。在平行投影中，我們指定投影方向而不是投影中心。

在平行投影中，投影中心到投影平面的距離是無限大的。在這種型別的投影中，我們用線段連線投影頂點，這些線段對應於原始物體上的連線。

平行投影不太逼真，但它們有利於精確測量。在這種型別的投影中，平行線保持平行，但角度不保持不變。各種型別的平行投影如下所示。

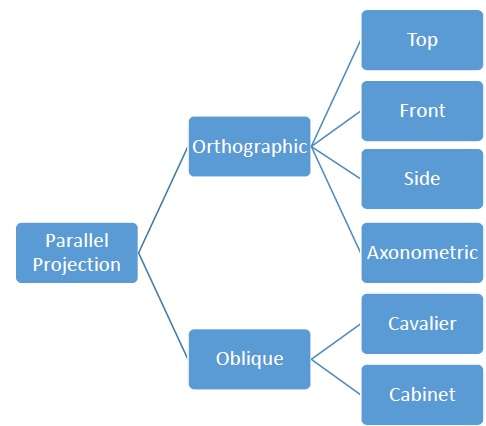
正投影

在正投影中，投影方向垂直於投影平面。正投影有三種類型：

正面投影
頂面投影
側面投影

斜投影

在斜投影中，投影方向不垂直於投影平面。在斜投影中，我們可以比正投影更好地觀察物體。

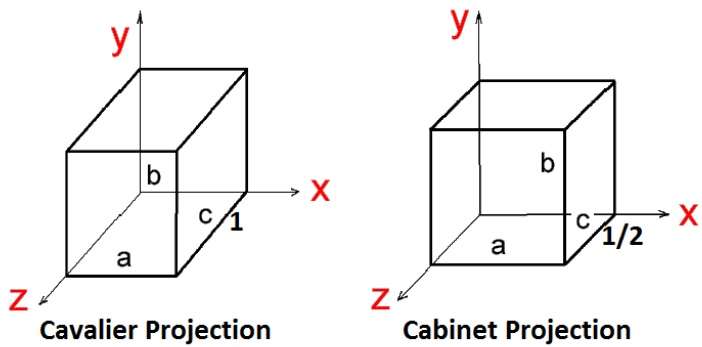
斜投影有兩種型別：**騎士投影**和**內閣投影**。騎士投影與投影平面成 45° 角。在騎士投影中，垂直於視平面的線的投影長度與其本身相同。在騎士投影中，所有三個主要方向的縮短因子都相等。

內閣投影與投影平面成 63.4° 角。在內閣投影中，垂直於觀察表面的線以其實際長度的一半投影。下圖顯示了這兩種投影：

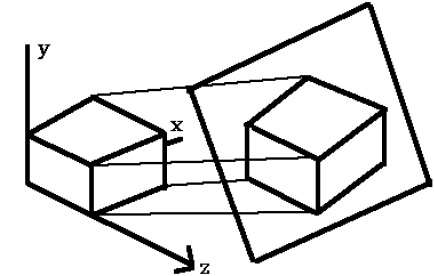
等軸測投影

顯示物體多個側面的正投影稱為**軸測正投影**。最常見的軸測投影是**等軸測投影**，其中投影平面在模型座標系中與每個座標軸相交於等距。在這種投影中，線的平行性保持不變，但角度不保持不變。下圖顯示了等軸測投影：

透視投影

在透視投影中，投影中心到投影平面的距離是有限的，物體的尺寸與距離成反比，看起來更逼真。

距離和角度不保持不變，平行線也不保持平行。相反，它們都匯聚在一個點上，這個點稱為**投影中心**或**投影參考點**。透視投影有三種類型，如下表所示。

**一點**透視投影易於繪製。
**兩點**透視投影能更好地展現深度感。
**三點**透視投影最難繪製。

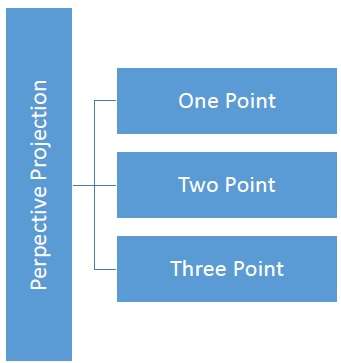
下圖顯示了三種透視投影：

平移

在三維平移中，我們除了 X 和 Y 座標外，還要平移 Z 座標。三維平移的過程與二維平移類似。平移將物體移動到螢幕上的不同位置。

下圖顯示了平移的效果：

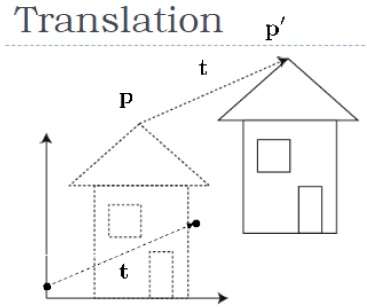
可以透過將平移座標 $(t_{x,} t_{y,} t_{z})$ 新增到原始座標 (X, Y, Z) 來平移三維空間中的點，從而得到新的座標 (X', Y', Z')。

$T = \begin{bmatrix} 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ t_{x}& t_{y}& t_{z}& 1\\ \end{bmatrix}$

P’ = P∙T

$[X′ \:\: Y′ \:\: Z′ \:\: 1] \: = \: [X \:\: Y \:\: Z \:\: 1] \: \begin{bmatrix} 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ t_{x}& t_{y}& t_{z}& 1\\ \end{bmatrix}$

$= [X + t_{x} \:\:\: Y + t_{y} \:\:\: Z + t_{z} \:\:\: 1]$

三維變換

旋轉

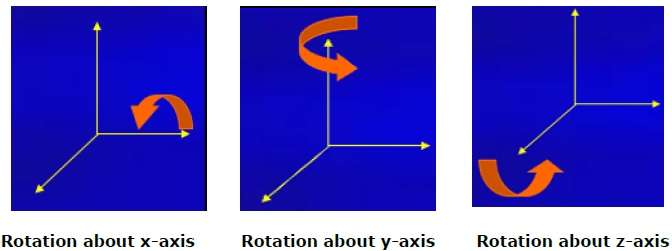
三維旋轉與二維旋轉不同。在三維旋轉中，我們必須指定旋轉角度以及旋轉軸。我們可以圍繞 X、Y 和 Z 軸進行三維旋轉。它們以矩陣形式表示如下：

$$R_{x}(\theta) = \begin{bmatrix} 1& 0& 0& 0\\ 0& \cos\theta & -\sin\theta& 0\\ 0& \sin\theta & \cos\theta& 0\\ 0& 0& 0& 1\\ \end{bmatrix} R_{y}(\theta) = \begin{bmatrix} \cos\theta& 0& \sin\theta& 0\\ 0& 1& 0& 0\\ -\sin\theta& 0& \cos\theta& 0\\ 0& 0& 0& 1\\ \end{bmatrix} R_{z}(\theta) =\begin{bmatrix} \cos\theta & -\sin\theta & 0& 0\\ \sin\theta & \cos\theta & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1 \end{bmatrix}$$

下圖解釋了圍繞各個軸的旋轉：

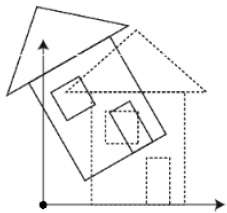
縮放

您可以使用縮放變換來更改物件的大小。在縮放過程中，您可以擴充套件或壓縮物件的尺寸。縮放可以透過將物件的原始座標乘以縮放因子來獲得所需的結果。下圖顯示了三維縮放的效果：

在三維縮放操作中，使用三個座標。假設原始座標為 (X, Y, Z)，縮放因子分別為 $(S_{X,} S_{Y,} S_{z})$，生成的座標為 (X', Y', Z')。這可以用下面的數學公式表示：

$S = \begin{bmatrix} S_{x}& 0& 0& 0\\ 0& S_{y}& 0& 0\\ 0& 0& S_{z}& 0\\ 0& 0& 0& 1 \end{bmatrix}$

P’ = P∙S

$[{X}' \:\:\: {Y}' \:\:\: {Z}' \:\:\: 1] = [X \:\:\:Y \:\:\: Z \:\:\: 1] \:\: \begin{bmatrix} S_{x}& 0& 0& 0\\ 0& S_{y}& 0& 0\\ 0& 0& S_{z}& 0\\ 0& 0& 0& 1 \end{bmatrix}$

$ = [X.S_{x} \:\:\: Y.S_{y} \:\:\: Z.S_{z} \:\:\: 1]$

錯切

使物體形狀傾斜的變換稱為**剪下變換**。與二維剪下一樣，我們可以在三維空間中沿 X 軸、Y 軸或 Z 軸剪下物體。

如上圖所示，有一個座標 P。您可以剪下它以獲得新的座標 P'，這可以用三維矩陣形式表示如下：

$Sh = \begin{bmatrix} 1 & sh_{x}^{y} & sh_{x}^{z} & 0 \\ sh_{y}^{x} & 1 & sh_{y}^{z} & 0 \\ sh_{z}^{x} & sh_{z}^{y} & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$

P’ = P ∙ Sh

X’ = X + Sh_{x}^{y} Y + Sh_{x}^{z} Z

Y' = Sh_{y}^{x}X + Y +sh_{y}^{z}Z

Z' = Sh_{z}^{x}X + Sh_{z}^{y}Y + Z

變換矩陣

變換矩陣是變換的基本工具。一個 n x m 維的矩陣與物體的座標相乘。通常使用 3 x 3 或 4 x 4 矩陣進行變換。例如，考慮以下用於各種操作的矩陣。

$T = \begin{bmatrix} 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ t_{x}& t_{y}& t_{z}& 1\\ \end{bmatrix}$	$S = \begin{bmatrix} S_{x}& 0& 0& 0\\ 0& S_{y}& 0& 0\\ 0& 0& S_{z}& 0\\ 0& 0& 0& 1 \end{bmatrix}$	$Sh = \begin{bmatrix} 1& sh_{x}^{y}& sh_{x}^{z}& 0\\ sh_{y}^{x}& 1 & sh_{y}^{z}& 0\\ sh_{z}^{x}& sh_{z}^{y}& 1& 0\\ 0& 0& 0& 1 \end{bmatrix}$
平移矩陣	縮放矩陣	剪下矩陣
$R_{x}(\theta) = \begin{bmatrix} 1& 0& 0& 0\\ 0& \cos\theta & -\sin\theta& 0\\ 0& \sin\theta & \cos\theta& 0\\ 0& 0& 0& 1\\ \end{bmatrix}$	$R_{y}(\theta) = \begin{bmatrix} \cos\theta& 0& \sin\theta& 0\\ 0& 1& 0& 0\\ -\sin\theta& 0& \cos\theta& 0\\ 0& 0& 0& 1\\ \end{bmatrix}$	$R_{z}(\theta) = \begin{bmatrix} \cos\theta & -\sin\theta & 0& 0\\ \sin\theta & \cos\theta & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1 \end{bmatrix}$
旋轉矩陣

計算機圖形學曲線

在計算機圖形學中，我們經常需要將不同型別的物體繪製到螢幕上。物體並非總是平面的，我們常常需要繪製曲線來繪製物體。

曲線型別

曲線是無限大的點集。每個點都有兩個鄰居，除了端點。曲線可以大致分為三類：**顯式曲線、隱式曲線**和**引數曲線**。

隱式曲線

隱式曲線表示透過使用可以測試點是否在曲線上的過程來定義曲線上的點集。通常，隱式曲線由以下形式的隱函式定義：

f(x, y) = 0

它可以表示多值曲線（對於一個 x 值有多個 y 值）。一個常見的例子是圓，其隱式表示為

x² + y² - R² = 0

顯式曲線

數學函式 y = f(x) 可以繪製成曲線。這樣的函式是曲線的顯式表示。顯式表示不是通用的，因為它不能表示垂直線，並且也是單值的。對於每個 x 值，函式通常只計算一個 y 值。

引數曲線

具有引數形式的曲線稱為引數曲線。顯式和隱式曲線表示只有在已知函式時才能使用。實際上使用的是引數曲線。二維引數曲線具有以下形式：

P(t) = f(t), g(t) 或 P(t) = x(t), y(t)

函式 f 和 g 成為曲線任意點的 (x, y) 座標，當引數 t 在某個區間 [a, b]（通常為 [0, 1]）內變化時，可以得到這些點。

貝塞爾曲線

貝塞爾曲線是由法國工程師**皮埃爾·貝塞爾**發現的。這些曲線可以在其他點的控制下生成。使用控制點逼近切線來生成曲線。貝塞爾曲線可以用數學方法表示為：

$$ \sum_{k=0}^{n} P_{i}{B_{i}^{n}}(t) $$

其中 $p_{i}$ 是點集，${B_{i}^{n}}(t)$ 表示伯恩斯坦多項式，其由下式給出：

$$ {B_{i}^{n}}(t) = \binom{n}{i} (1 - t)^{n-i}t^{i} $$

其中**n**是多項式的次數，**i**是索引，**t**是變數。

最簡單的貝塞爾曲線是從點 $P_{0}$ 到 $P_{1}$ 的直線。二次貝塞爾曲線由三個控制點確定。三次貝塞爾曲線由四個控制點確定。

貝塞爾曲線的性質

貝塞爾曲線具有以下性質：

它們通常遵循控制多邊形的形狀，控制多邊形由連線控制點的線段組成。
它們總是透過第一個和最後一個控制點。
它們包含在其定義控制點的凸包中。
定義曲線段的多項式的次數比定義多邊形的點數少 1。因此，對於 4 個控制點，多項式的次數為 3，即三次多項式。
貝塞爾曲線通常遵循定義多邊形的形狀。
端點處切向量的方向與由第一段和最後一段確定的向量方向相同。
貝塞爾曲線的凸包性質確保多項式平滑地跟隨控制點。
任何直線與貝塞爾曲線相交的次數不超過它與控制多邊形相交的次數。
它們在仿射變換下是不變的。
貝塞爾曲線具有全域性控制性，這意味著移動一個控制點會改變整個曲線形狀。
給定的貝塞爾曲線可以在點t=t0處細分為兩段貝塞爾曲線段，這兩段曲線段在對應於引數值t=t0的點處連線在一起。

B樣條曲線

由伯恩斯坦基函式生成的貝塞爾曲線靈活性有限。

首先，指定的polygon頂點數決定了定義曲線的最終多項式的階數。
第二個限制特性是，混合函式的值在整個曲線上的所有引數值上都不為零。

B樣條基包含伯恩斯坦基作為特例。B樣條基是非全域性的。

B樣條曲線定義為控制點Pi和B樣條基函式$N_{i,}$ k (t)的線性組合，如下所示：

$C(t) = \sum_{i=0}^{n}P_{i}N_{i,k}(t),$ $n\geq k-1,$ $t\: \epsilon \: [ tk-1,tn+1 ]$

其中，

{$p_{i}$: i=0, 1, 2….n} 為控制點
k是B樣條曲線的多分段多項式的階數。k階意味著曲線由k-1次的分段多項式段組成。
$N_{i,k}(t)$是“歸一化B樣條混合函式”。它們由階數k和一組非遞減的實數（通常稱為“節點序列”）描述。

$${t_{i}:i = 0, ... n + K}$$

N_i, k函式描述如下：

$$N_{i,1}(t) = \left\{\begin{matrix} 1,& if \:u \: \epsilon \: [t_{i,}t_{i+1}) \\ 0,& 其他 \end{matrix}\right.$$

如果k > 1，則

$$N_{i,k}(t) = \frac{t-t_{i}}{t_{i+k-1}-t_i} N_{i,k-1}(t) + \frac{t_{i+k}-t}{t_{i+k} - t_{i+1}} N_{i+1,k-1}(t)$$

和

$$t \: \epsilon \: [t_{k-1},t_{n+1})$$

B樣條曲線的性質

B樣條曲線具有以下性質：

對於任何引數值，B樣條基函式之和為1。
每個基函式對於所有引數值都為正或零。
除k=1外，每個基函式只有一個最大值。
曲線的最大階數等於定義多邊形的頂點數。
B樣條多項式的次數與定義多邊形的頂點數無關。
B樣條允許對曲線表面進行區域性控制，因為每個頂點隻影響其相關基函式非零的引數值範圍內的曲線形狀。
曲線表現出變化遞減特性。
曲線通常遵循定義多邊形的形狀。
可以透過將其應用於定義多邊形的頂點來將任何仿射變換應用於曲線。
曲線位於其定義多邊形的凸包內。

計算機圖形學曲面

多邊形曲面

物體表示為曲面的集合。3D物體表示分為兩類。

邊界表示法 (B-reps) − 它將3D物體描述為一組將物體內部與環境隔開的曲面。
空間劃分表示法 − 透過將包含物體的空間區域劃分為一組小的、不重疊的、連續的實體（通常是立方體）來描述內部屬性。

最常用的3D圖形物體的邊界表示法是一組封閉物體內部的表面多邊形。許多圖形系統都使用這種方法。儲存多邊形集合用於物體描述。這簡化並加快了物體的表面渲染和顯示，因為所有曲面都可以用線性方程描述。

多邊形曲面在設計和實體建模應用中很常見，因為它們的線框顯示可以快速完成，從而可以大致指示表面結構。然後透過在多邊形表面上插值陰影圖案來產生逼真的場景以進行照明。

多邊形表

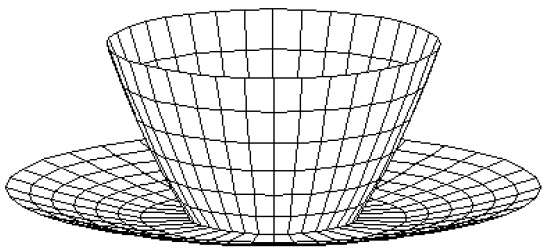
在這種方法中，曲面由頂點座標集和相關屬性指定。如下圖所示，有五個頂點，從v₁到v₅。

每個頂點儲存x、y和z座標資訊，在表中表示為v₁: x₁, y₁, z₁。
邊表用於儲存多邊形的邊資訊。在下圖中，邊E₁位於頂點v₁和v₂之間，在表中表示為E₁: v₁, v₂。
多邊形曲面表儲存多邊形中存在的曲面數量。從下圖可以看出，曲面S₁由邊E₁、E₂和E₃覆蓋，這可以在多邊形曲面表中表示為S₁: E₁, E₂和E₃。

平面方程

平面曲面的方程可以表示為：

Ax + By + Cz + D = 0

其中(x, y, z)是平面上的任意一點，係數A、B、C和D是描述平面空間屬性的常數。我們可以透過使用平面中三個非共線點的座標值求解一組三個平面方程來獲得A、B、C和D的值。讓我們假設平面的三個頂點是(x₁, y₁, z₁)、(x₂, y₂, z₂)和(x₃, y₃, z₃)。

讓我們求解以下聯立方程以求A/D、B/D和C/D的比率。你可以得到A、B、C和D的值。

(A/D) x₁ + (B/D) y₁ + (C/D) z₁ = -1

(A/D) x₂ + (B/D) y₂ + (C/D) z₂ = -1

(A/D) x₃ + (B/D) y₃ + (C/D) z₃ = -1

為了以行列式形式獲得上述方程，將克萊姆法則應用於上述方程。

$A = \begin{bmatrix} 1& y_{1}& z_{1}\\ 1& y_{2}& z_{2}\\ 1& y_{3}& z_{3} \end{bmatrix} B = \begin{bmatrix} x_{1}& 1& z_{1}\\ x_{2}& 1& z_{2}\\ x_{3}& 1& z_{3} \end{bmatrix} C = \begin{bmatrix} x_{1}& y_{1}& 1\\ x_{2}& y_{2}& 1\\ x_{3}& y_{3}& 1 \end{bmatrix} D = - \begin{bmatrix} x_{1}& y_{1}& z_{1}\\ x_{2}& y_{2}& z_{2}\\ x_{3}& y_{3}& z_{3} \end{bmatrix}$

對於具有引數A、B、C和D的任何點(x, y, z)，我們可以說：

Ax + By + Cz + D ≠ 0 表示該點不在平面上。
Ax + By + Cz + D < 0 表示該點在曲面內部。
Ax + By + Cz + D > 0 表示該點在曲面外部。

多邊形網格

3D曲面和實體可以用一組多邊形和線元素來近似。這種曲面稱為多邊形網格。在多邊形網格中，每條邊最多由兩個多邊形共享。多邊形或面的集合共同構成物體的“外殼”。

此方法可用於表示圖形中各種實體/曲面。可以使用隱藏曲面消除演算法渲染多邊形網格。多邊形網格可以用三種方式表示：

顯式表示
指向頂點列表的指標
指向邊列表的指標

優點

它可用於模擬幾乎任何物體。
它們很容易表示為頂點的集合。
它們很容易轉換。
它們很容易在電腦螢幕上繪製。

缺點

只能近似描述曲線曲面。
很難模擬某些型別的物體，例如頭髮或液體。

可見面檢測

當我們檢視包含非透明物體和曲面的圖片時，我們無法看到那些位於更靠近眼睛的物體後面的物體。我們必須去除這些隱藏曲面才能獲得逼真的螢幕影像。這些曲面的識別和去除稱為隱藏曲面問題。

去除隱藏曲面問題有兩種方法：物體空間方法和影像空間方法。物體空間方法在物理座標系中實現，影像空間方法在螢幕座標系中實現。

當我們想在二維螢幕上顯示三維物體時，我們需要識別從選擇的觀察位置可見的螢幕部分。

深度緩衝區 (Z-緩衝區) 方法

此方法由Cutmull開發。這是一種影像空間方法。其基本思想是測試每個曲面的Z深度以確定最接近（可見）的曲面。

在此方法中，每個曲面都單獨處理，一次一個畫素位置地跨越曲面。比較畫素的深度值，最接近（最小z）的曲面決定要在幀緩衝區中顯示的顏色。

它在多邊形的曲面上非常有效地應用。曲面可以以任何順序處理。為了覆蓋靠近的多邊形，使用名為幀緩衝區和深度緩衝區的兩個緩衝區。

深度緩衝區用於儲存曲面處理時(x, y)位置的深度值 (0 ≤ depth ≤ 1)。

幀緩衝區用於儲存每個位置(x, y)的顏色值的強度值。

z座標通常歸一化為[0, 1]範圍。z座標的0值表示後裁剪平面，z座標的1值表示前裁剪平面。

演算法

步驟1 − 設定緩衝區值：

Depthbuffer (x, y) = 0

Framebuffer (x, y) = 背景顏色

步驟2 − 處理每個多邊形（一次一個）

對於多邊形的每個投影的(x, y)畫素位置，計算深度z。

如果Z > depthbuffer (x, y)

計算曲面顏色，

設定depthbuffer (x, y) = z，

framebuffer (x, y) = surfacecolor (x, y)

優點

易於實現。
如果在硬體中實現，則可以減少速度問題。
它一次處理一個物件。

缺點

它需要大量的記憶體。
這是一個耗時的過程。

掃描線方法

這是一種識別可見曲面的影像空間方法。此方法僅對單個掃描線具有深度資訊。為了需要一條掃描線的深度值，我們必須在處理下一條掃描線之前，同時對相交於給定掃描線的全部多邊形進行分組和處理。為此，維護兩個重要的表：邊表和多邊形表。

邊表 − 它包含場景中每條線的座標端點、每條線的反斜率以及指向多邊形表的指標，以將邊連線到曲面。

多邊形表 − 它包含平面係數、表面材質屬性、其他表面資料，並且可能是指向邊表的指標。

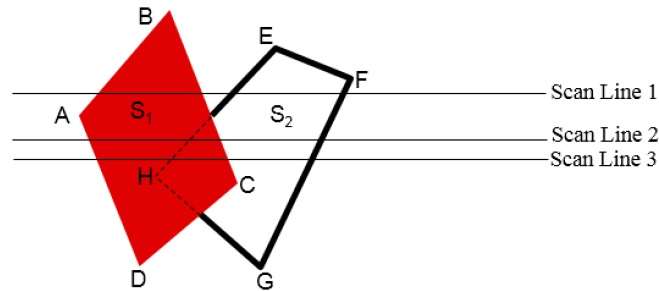
為了方便搜尋穿過給定掃描線的表面，會形成一個活動的邊列表。活動列表僅儲存按 x 值遞增順序排列的、與掃描線相交的那些邊。此外，還會為每個表面設定一個標誌，以指示掃描線上的某個位置是在表面內部還是外部。

每個掃描線上的畫素位置都是從左到右處理的。在與表面的左側交點處，表面標誌被開啟；在右側交點處，標誌被關閉。只有當多個表面的標誌在某個掃描線位置都被開啟時，才需要執行深度計算。

區域細分法

區域細分法透過定位代表單個表面一部分的那些視區來發揮優勢。將總視區細分為越來越小的矩形，直到每個小區都是單個可見表面的投影部分或根本沒有表面。

繼續此過程，直到細分很容易被分析為屬於單個表面，或者直到它們被縮小到單個畫素的大小。一個簡單的做法是在每一步都將區域連續地細分為四個相等的部分。表面可能與指定的區域邊界具有四種可能的關聯。

包圍表面 − 完全包圍該區域的表面。
重疊表面 − 部分在區域內，部分在區域外的表面。
內部表面 − 完全在區域內的表面。
外部表面 − 完全在區域外的表面。

確定區域內表面可見性的測試可以用這四種分類來表示。如果以下條件之一為真，則不需要對指定區域進行進一步細分 −

所有表面相對於該區域都是外部表面。
該區域內只有一個內部、重疊或包圍表面。
包圍表面遮擋了區域邊界內的所有其他表面。

背面檢測

一種快速簡單的物件空間方法，用於識別多面體的背面，基於“內外”測試。如果點 (x, y, z) 滿足平面引數 A、B、C 和 D 的多邊形表面“內部”條件，則當內部點位於視線與表面的連線上時，多邊形必須是背面（我們在這個面內，無法從我們的觀看位置看到它的正面）。

我們可以透過考慮多邊形表面的法向量N 來簡化此測試，該法向量具有笛卡爾分量 (A, B, C)。

一般來說，如果 V 是從眼睛（或“相機”）位置朝觀看方向的向量，則如果以下條件成立，則該多邊形為背面

V.N > 0

此外，如果物件描述被轉換為投影座標，並且您的觀看方向平行於觀看 z 軸，則 −

V = (0, 0, V_z) 並且 V.N = V_ZC

這樣我們只需要考慮法向量N的分量 C 的符號。

在右手系觀看系統中，觀看方向沿負 $Z_{V}$ 軸，如果 C < 0，則多邊形為背面。此外，我們無法看到法向量 z 分量 C = 0 的任何面，因為您的觀看方向朝向該多邊形。因此，一般來說，如果多邊形的法向量的 z 分量值為 −，我們可以將任何多邊形標記為背面

C <= 0

類似的方法可用於採用左手系觀看系統的包。在這些包中，平面引數 A、B、C 和 D 可以根據以順時針方向指定的（與右手系中使用的逆時針方向不同）多邊形頂點座標計算。

此外，背面法向量指向遠離觀看位置，當觀看方向沿正 $Z_{v}$ 軸時，由 C >= 0 標識。透過檢查定義物件的不同平面的引數 C，我們可以立即識別所有背面。

A 緩衝區方法

A 緩衝區方法是深度緩衝區方法的擴充套件。A 緩衝區方法是由盧卡斯影業為渲染系統 Renders Everything You Ever Saw (REYES) 開發的一種可見性檢測方法。

A 緩衝區擴充套件了深度緩衝區方法以允許透明度。A 緩衝區中的關鍵資料結構是累積緩衝區。

A 緩衝區中的每個位置都有兩個欄位 −

深度欄位 − 它儲存一個正數或負數。
強度欄位 − 它儲存表面強度資訊或指標值。

如果深度 >= 0，則該位置儲存的數字是與相應畫素區域重疊的單個表面的深度。然後，強度欄位儲存該點表面顏色的 RGB 分量和畫素覆蓋百分比。

如果深度 < 0，則表示對畫素強度有多個表面的貢獻。然後，強度欄位儲存指向表面資料的連結串列的指標。A 緩衝區中的表面緩衝區包括 −

RGB 強度分量
不透明度引數
深度
面積覆蓋百分比
表面識別符號

演算法的執行方式與深度緩衝區演算法相同。深度和不透明度值用於確定畫素的最終顏色。

深度排序法

深度排序法同時使用影像空間和物件空間操作。深度排序法執行兩個基本功能 −

首先，按深度遞減的順序對錶面進行排序。
其次，按順序掃描轉換表面，從深度最大的表面開始。

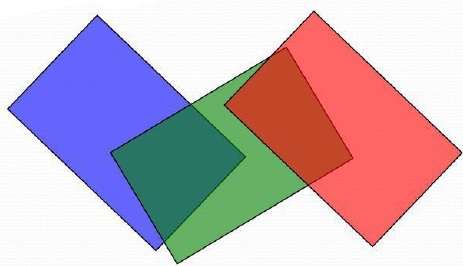
多邊形表面的掃描轉換在影像空間中執行。這種解決隱藏面問題的的方法通常被稱為畫家演算法。下圖顯示了深度排序的效果 −

演算法首先按深度排序。例如，多邊形的初始“深度”估計可以取為多邊形的任何頂點的最近 z 值。

讓我們取列表末尾的多邊形 P。考慮所有其 z 範圍與 P 重疊的多邊形 Q。在繪製 P 之前，我們進行以下測試。如果任何以下測試為正，則我們可以假設可以在 Q 之前繪製 P。

x 範圍是否不重疊？
y 範圍是否不重疊？
P 是否完全位於 Q 平面與視點相對的一側？
Q 是否完全位於 P 平面的與視點相同的一側？
多邊形的投影是否不重疊？

如果所有測試都失敗，則使用另一個平面對 P 或 Q 進行分割。將新的切割多邊形插入深度順序中，並繼續該過程。理論上，這種分割槽可能會生成 O(n²) 個單獨的多邊形，但在實踐中，多邊形的數量要少得多。

二元空間劃分 (BSP) 樹

二元空間劃分用於計算可見性。要構建 BSP 樹，應從多邊形開始並標記所有邊。一次只處理一條邊，擴充套件每條邊使其將平面分成兩部分。將第一條邊作為根節點放入樹中。根據後續邊是在內部還是外部新增後續邊。跨越已在樹中的邊的擴充套件的邊被分成兩部分，並且兩者都被新增到樹中。

從上圖來看，首先取A作為根。
列出圖 (a) 中的所有節點。
將所有位於根節點A前面的節點放在節點A的左側，並將所有位於根節點A後面的節點放在右側，如圖 (b) 所示。
首先處理所有前面的節點，然後處理後面的節點。
如圖 (c) 所示，我們將首先處理節點B。由於節點B前面沒有任何內容，因此我們已放置 NIL。但是，我們在節點B的後面有節點C，因此節點C將位於節點B的右側。
對節點D重複相同的過程。

計算機圖形學分形

法國/美國數學家 Benoit Mandelbrot 博士發現了分形。分形一詞源於拉丁詞fractus，意思是破碎的。

什麼是分形？

分形是由計算機根據單個公式生成的非常複雜的影像。它們是使用迭代建立的。這意味著一個公式會一遍又一遍地使用略微不同的值重複，同時考慮來自先前迭代的結果。

分形用於許多領域，例如 −

天文學 − 用於分析星系、土星環等。
生物學/化學 − 用於描繪細菌培養物、化學反應、人體解剖結構、分子、植物等。
其他 − 用於描繪雲、海岸線和邊界線、資料壓縮、擴散、經濟、分形藝術、分形音樂、景觀、特效等。

分形的生成

分形可以透過反覆重複相同的形狀來生成，如下圖所示。圖 (a) 顯示了一個等邊三角形。在圖 (b) 中，我們可以看到三角形被重複以建立星形。在圖 (c) 中，我們可以看到圖 (b) 中的星形被反覆重複以建立新的形狀。

我們可以進行無限次的迭代來建立所需的形狀。在程式設計方面，使用遞迴來建立此類形狀。

幾何分形

幾何分形處理自然界中具有非整數或分形維度的形狀。為了幾何地構造確定性（非隨機）自相似分形，我們從給定的幾何形狀（稱為起始體）開始。然後用稱為生成器的圖案替換起始體的子部分。

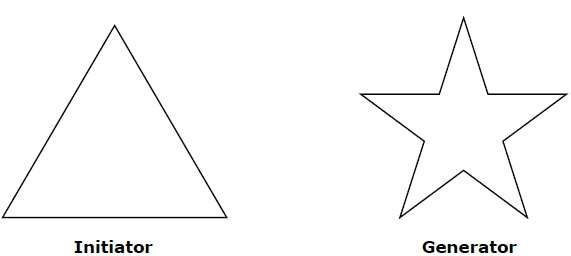
例如，如果我們使用上圖中所示的起始體和生成器，我們可以透過重複它來構造良好的圖案。起始體中的每一段直線段在每一步都由四段等長線段替換。比例因子為 1/3，因此分形維數為 D = ln 4/ln 3 ≈ 1.2619。

此外，起始體中每段線段的長度在每一步都增加 4/3 倍，因此隨著曲線中新增更多細節，分形曲線的長度趨於無窮大，如下圖所示 −

計算機動畫

動畫意味著在計算機圖形中賦予任何物件生命。它具有將能量和情感注入看似最無生命的物體中的能力。計算機輔助動畫和計算機生成的動畫是計算機動畫的兩個類別。它可以透過電影或影片呈現。

動畫背後的基本思想是以足夠快的速度播放錄製的影像，以欺騙人眼將其解釋為連續運動。動畫可以讓一系列靜態影像栩栩如生。動畫可用於許多領域，例如娛樂、計算機輔助設計、科學視覺化、培訓、教育、電子商務和計算機藝術。

動畫技術

動畫師發明並使用了各種不同的動畫技術。基本上有六種動畫技術，我們將在本節中逐一討論。

傳統動畫（逐幀）

傳統上，大部分動畫都是手工完成的。動畫中的所有幀都必須手工繪製。由於每秒動畫需要 24 幀（膠片），因此即使是最短的電影的創作也需要付出巨大的努力。

關鍵幀動畫

在這種技術中，會繪製出故事板，然後藝術家繪製動畫的主要幀。主要幀是發生突出變化的幀。它們是動畫的關鍵點。關鍵幀動畫要求動畫師指定物件的關鍵位置。然後計算機透過在這些位置之間平滑插值來自動填充缺失的幀。

過程動畫

在過程動畫中，物件是透過過程（一組規則）而不是關鍵幀動畫來動畫的。動畫師指定規則和初始條件並執行模擬。規則通常基於用數學方程式表達的現實世界的物理規則。

行為動畫

在行為動畫中，自主角色至少在某種程度上決定自己的動作。這賦予角色一定的即興發揮能力，並使動畫師無需指定每個角色動作的每一個細節。

基於表演（動作捕捉）

另一種技術是動作捕捉，其中基於磁力或視覺的感測器以三維方式記錄人和動物物件的動作。然後，計算機使用這些資料來為物件製作動畫。

這項技術使許多著名運動員能夠為體育影片遊戲中的人物提供動作。動作捕捉在動畫師中非常流行，主要是因為一些常見的 human actions 可以相對容易地捕捉到。然而，主體和圖形角色的形狀或尺寸之間可能存在嚴重差異，這可能導致精確執行方面的問題。

基於物理（動力學）

與關鍵幀動畫和電影不同，模擬使用物理定律來生成影像和其他物件的運動。模擬可以很容易地用於生成略微不同的序列，同時保持物理真實感。其次，即時模擬允許更高程度的互動性，真人可以操縱模擬角色的動作。

相比之下，基於關鍵幀和動作的應用程式從預先計算的動作庫中選擇和修改動作。模擬的一個缺點是需要專業知識和時間來手工製作合適的控制系統。

關鍵幀

關鍵幀是在我們定義動畫變化的幀。當我們建立逐幀動畫時，每一幀都是關鍵幀。當有人在計算機上建立 3D 動畫時，他們通常不會指定任何給定物件在每一幀上的精確位置。他們建立關鍵幀。

關鍵幀是物件改變其大小、方向、形狀或其他屬性的重要幀。然後，計算機計算出所有中間幀，從而為動畫師節省大量時間。下圖描繪了使用者繪製的幀和計算機生成的幀。

變形

物體形狀從一種形式轉變為另一種形式的過程稱為變形。這是最複雜的變換之一。

變形看起來像是兩幅影像以非常流暢的動作融為一體。從技術角度來看，兩幅影像會發生扭曲，並在它們之間發生淡入淡出。

列印頁面