計算機圖形學分形

法國/美國數學家Benoit Mandelbrot博士發現了分形。 “分形”一詞源於拉丁詞fractus，意思是破碎的。

什麼是計算機圖形學中的分形？

分形是由計算機根據單個公式生成的非常複雜的影像。它們是使用迭代建立的。這意味著一個公式會反覆使用略微不同的值重複，並考慮來自先前迭代的結果。

分形被用於許多領域，例如：

• 天文學 - 用於分析星系、土星環等。

• 生物學/化學 - 用於描繪細菌培養物、化學反應、人體解剖結構、分子、植物等。

• 其他 - 用於描繪雲、海岸線和邊界線、資料壓縮、擴散、經濟、分形藝術、分形音樂、景觀、特效等。

計算機圖形學分形的生成

分形可以透過反覆重複相同的形狀來生成，如下圖所示。圖(a)顯示了一個等邊三角形。在圖(b)中，我們可以看到三角形被重複以建立一個星形。在圖(c)中，我們可以看到圖(b)中的星形被反覆重複以建立一個新的形狀。

我們可以進行無限次的迭代來建立所需的形狀。在程式設計方面，遞迴用於建立此類形狀。

幾何分形

幾何分形處理的是自然界中具有非整數或分形維度的形狀。為了幾何地構造一個確定性（非隨機）自相似分形，我們從一個給定的幾何形狀開始，稱為起始圖形。然後用一個圖案替換起始圖形的子部分，該圖案稱為生成器。

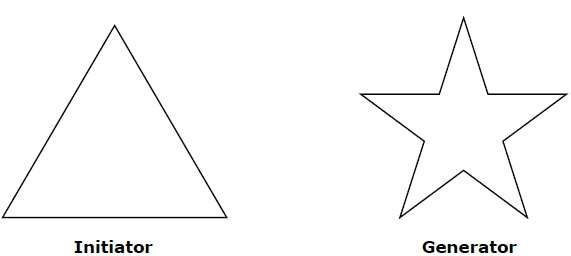
例如，如果我們使用上圖所示的起始圖形和生成器，我們可以透過重複它來構建良好的圖案。起始圖形中的每一段直線段在每一步都用四段等長的線段替換。縮放因子為1/3，因此分形維數為D = ln 4/ln 3 ≈ 1.2619。

此外，起始圖形中每條線段的長度在每一步都增加4/3倍，因此隨著向曲線新增更多細節，分形曲線的長度趨於無窮大，如下圖所示：