
計算機圖形學 - 圓生成演算法
在螢幕上繪製圓圈比繪製直線稍微複雜一些。有兩種流行的圓生成演算法:**Bresenham 演算法**和**中點圓演算法**。這些演算法基於確定繪製圓圈所需的後續點的思想。讓我們詳細討論這些演算法:
圓的方程為 $X^{2} + Y^{2} = r^{2}$,其中 r 是半徑。
Bresenham 演算法
我們無法在光柵顯示器上顯示連續的圓弧。相反,我們必須選擇最接近的畫素位置來完成圓弧。
從下圖中,您可以看到我們已將畫素置於 (X, Y) 位置,現在需要決定將下一個畫素置於何處:N (X+1, Y) 還是 S (X+1, Y-1)。

這可以透過決策引數 **d** 來決定。
- 如果 d <= 0,則選擇 N(X+1, Y) 作為下一個畫素。
- 如果 d > 0,則選擇 S(X+1, Y-1) 作為下一個畫素。
演算法
**步驟 1** - 獲取圓心和半徑的座標,並分別儲存在 x、y 和 R 中。設定 P=0 和 Q=R。
**步驟 2** - 設定決策引數 D = 3 – 2R。
**步驟 3** - 當 P ≤ Q 時,重複執行步驟 4 到步驟 8。
**步驟 4** - 呼叫 Draw Circle (X, Y, P, Q)。
**步驟 5** - 增加 P 的值。
**步驟 6** - 如果 D < 0,則 D = D + 4P + 6。
**步驟 7** - 否則,設定 R = R - 1,D = D + 4(P-Q) + 10。
**步驟 8** - 呼叫 Draw Circle (X, Y, P, Q)。
Draw Circle Method(X, Y, P, Q). Call Putpixel (X + P, Y + Q). Call Putpixel (X - P, Y + Q). Call Putpixel (X + P, Y - Q). Call Putpixel (X - P, Y - Q). Call Putpixel (X + Q, Y + P). Call Putpixel (X - Q, Y + P). Call Putpixel (X + Q, Y - P). Call Putpixel (X - Q, Y - P).
中點演算法
**步驟 1** - 輸入半徑 **r** 和圓心 $(x_{c,} y_{c})$,並獲得以原點為中心的圓周上的第一個點,如下所示:
(x0, y0) = (0, r)
**步驟 2** - 計算決策引數的初始值,如下所示:
$P_{0}$ = 5/4 – r(有關此方程式的簡化,請參見以下說明。)
f(x, y) = x2 + y2 - r2 = 0
f(xi - 1/2 + e, yi + 1)
= (xi - 1/2 + e)2 + (yi + 1)2 - r2
= (xi- 1/2)2 + (yi + 1)2 - r2 + 2(xi - 1/2)e + e2
= f(xi - 1/2, yi + 1) + 2(xi - 1/2)e + e2 = 0
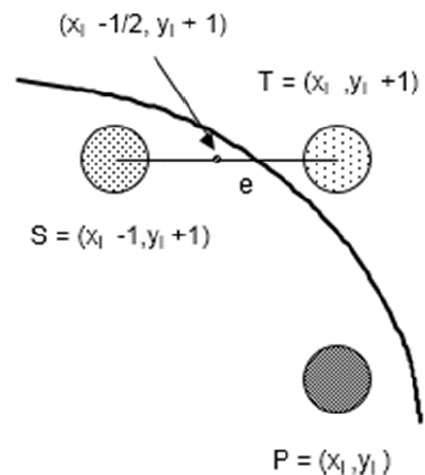
Let di = f(xi - 1/2, yi + 1) = -2(xi - 1/2)e - e2
Thus,
If e < 0 then di > 0 so choose point S = (xi - 1, yi + 1).
di+1 = f(xi - 1 - 1/2, yi + 1 + 1) = ((xi - 1/2) - 1)2 + ((yi + 1) + 1)2 - r2
= di - 2(xi - 1) + 2(yi + 1) + 1
= di + 2(yi + 1 - xi + 1) + 1
If e >= 0 then di <= 0 so choose point T = (xi, yi + 1)
di+1 = f(xi - 1/2, yi + 1 + 1)
= di + 2yi+1 + 1
The initial value of di is
d0 = f(r - 1/2, 0 + 1) = (r - 1/2)2 + 12 - r2
= 5/4 - r {1-r can be used if r is an integer}
When point S = (xi - 1, yi + 1) is chosen then
di+1 = di + -2xi+1 + 2yi+1 + 1
When point T = (xi, yi + 1) is chosen then
di+1 = di + 2yi+1 + 1
**步驟 3** - 從 K=0 開始,在每個 $X_{K}$ 位置執行以下測試:
If PK < 0 then next point on circle (0,0) is (XK+1,YK) and PK+1 = PK + 2XK+1 + 1 Else PK+1 = PK + 2XK+1 + 1 – 2YK+1 Where, 2XK+1 = 2XK+2 and 2YK+1 = 2YK-2.
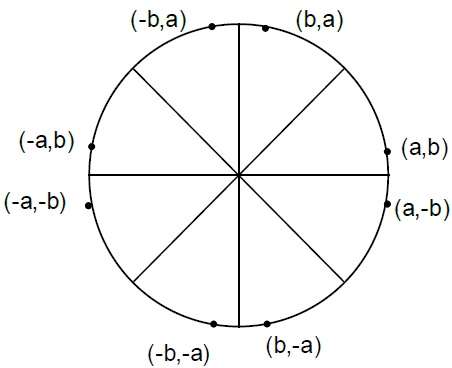
**步驟 4** - 確定其他七個象限中的對稱點。
**步驟 5** - 將每個計算出的畫素位置 (X, Y) 移動到以 $(X_{C,} Y_{C})$ 為中心的圓形路徑上,並繪製座標值。
X = X + XC, Y = Y + YC
**步驟 6** - 重複步驟 3 到步驟 5,直到 X >= Y。