規範分析 - 最佳化技術

規範分析是資料分析的一個子集，它利用預測模型來推薦行動以獲得最佳結果。規範分析演示瞭如何利用分析根據事實做出更好的決策。

例如，預測分析包括預測未來24小時內某個城市的暴雨，而規範分析則涉及回答如何用最佳資源來管理這種情況的問題。規範分析依賴於最佳化和基於規則的決策策略。

線性規劃、整數規劃和非線性規劃等最佳化技術在規範分析中非常重要，因為它們允許以最佳方式做出一系列決策。這些策略用於反映要做的決策、決策的限制以及比較決策的指標的模型。

規範分析利用最佳化和基於規則的策略來幫助做出更好的資料驅動決策。線性規劃和非線性規劃是規範分析中重要的技術，幫助組織做出資料驅動的決策。

1. 線性規劃

線性最佳化涉及用於最佳化線性目標函式的數學方法，受線性等式和不等式約束。它用於解決具有線性約束和目標的問題。該過程包括定義一個代表業務現實的模型，包括所有限制和約束。然後驗證模型以確保它反映業務現實。線性最佳化技術最廣泛地應用於供應鏈管理、生產計劃、運輸、金融和員工排班。

線性規劃的關鍵組成部分

目標函式 - 需要最大化或最小化的線性函式（例如，利潤、成本）。目標函式是一個線性方程，它描述了決策變數與要最佳化的結果之間的關係。例如 - 最大化 Z = c₁x₁+c₂x₂+...+c_nx_n 其中 Z 是要最大化的目標，x₁,x₂,...,x_n 是決策變數，c₁,c₂,...,c_n是係數。
決策變數 - 受控或被最佳化以達到最佳解決方案的變數。在規範分析中，這些決策變數可能表示要生成的產出數量、資源分配或產品分配。
約束條件 - 約束決策變數值的線性方程或不等式。這些約束表示為線性不等式或等式。例如：a₁x₁+a₂x₂+...+a_nx_n≤b 其中 b 是上限，a₁, a₂,..., a_n 是反映每個變數貢獻的係數。
可行域 - 可行域包含滿足約束條件的所有可行解。它通常是多維空間中的凸多面體。該區域中的任何點都可以用來解決最佳化問題。
最佳化解 - 目的是確定可行區域中最大化或最小化目標函式的位置。這是透過使用單純形法和內點法等技術來實現的。

線性最佳化

最佳化應用於公司的各個方面，包括運營、財務、人力資源和營銷。假設您管理一個小型造紙廠，需要確定所需的造紙量。當然，您可以根據您的產品需求做出選擇。為了提高銷售額和擴大產品規模，重要的是進行研究並評估需求和成本等方面。

如果一家公司每天生產數百種產品，那麼資料對於最佳化產品組合至關重要。這種最佳化並非旨在使生產過程更快或更便宜。我們感興趣的是我們需要生產多少。

線性最佳化的常見應用包括：

產品組合 - 選擇每種產品的適當數量進行生產和銷售。
計劃 - 根據供需預測選擇生產產品的時間，例如在節假日銷售旺季。
規劃投資組合 - 考慮投資選擇以最大化回報或最小化風險敞口，在指定的限制內。
最佳化勞動力分配 - 如何安排員工的輪班？
最佳化運輸和供應鏈 - 減少等待時間的路線。如何將產品從供應商轉移到倉庫再到分銷商，特別是對於易腐爛的商品。

線性最佳化的步驟

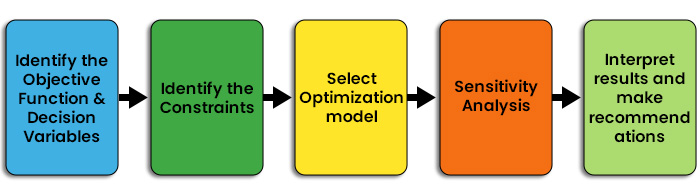
線性最佳化的應用

線性最佳化的關鍵應用領域如下：

供應鏈最佳化 - 透過使用最佳化模型，公司可以最佳化其供應鏈流程，包括但不限於庫存管理、運輸計劃和生產排程。
員工排班 - 醫院可以使用最佳化模型來找到護士和醫生的最佳排班方案，同時考慮輪班偏好、任務分配和工作量規定。
投資組合最佳化 - 金融機構利用最佳化模型來確定在多個投資機會中資金的最佳分配，同時考慮風險、回報和資產相關性。
車輛路徑規劃 - 可以使用最佳化模型來最佳化卡車路線和排程，同時考慮道路擁堵、送貨時間窗和車輛容量等因素。
生產計劃 - 可以使用最佳化模型來計算理想的生產計劃，同時考慮生產能力、原材料可用性和生產成本等因素。

2. 非線性規劃

非線性規劃包括在邊界約束、線性約束或非線性約束下最小化或最大化非線性目標函式，這些約束可以是不等式或等式。典型的工程挑戰包括檢查設計權衡、選擇最佳設計、計算最佳軌跡以及計算金融中的投資組合最佳化和模型校準。非線性最佳化關注目標函式或任何約束條件為非線性的問題。它用於解決具有非線性目標或約束的問題。例如，一家公司可以使用非線性最佳化技術來尋找在不同媒體上分配廣告費用的最佳方法；工程設計、投資組合最佳化、機器學習和其他科學領域。

非線性最佳化

規範分析中的非線性最佳化使用以下方法：

目標函式

非線性最佳化中的目標函式可以是一個非線性方程，您希望最大化（例如，利潤、效率）或最小化（例如，成本、誤差）。例如：

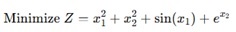
決策變數𝑥1, 𝑥2 和結果𝑍之間的關係不是直線。決策變數的小變化可能導致結果的複雜變化。

決策變數

受控或被最佳化以達到最佳解決方案的變數。在規範分析中，這些決策變數可能表示要生成的產出數量、資源分配或產品分配。

非線性約束

非線性約束是不等式或等式，它們與決策變數之間沒有線性關係。例如

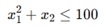
這些約束可能包括冪、指數、對數或其他非線性函式，使得可行域比線性問題更復雜。

可行域

可行域包含滿足約束條件的所有可行解。它通常是多維空間中的凸多面體。該區域中的任何點都可以用來解決最佳化問題。非線性最佳化中的可行區域可能具有複雜的邊界，而不是像線性最佳化中那樣是簡單的凸多面體。非凸區域可能具有多個區域性最優解（峰值和谷值），這意味著雖然許多位置在特定區域看起來是最優的，但只有一個才是真正的全域性最優解。

非凸問題

非凸問題在非線性最佳化中很常見。與凸問題相比，非凸問題可能有多個區域性最優解，因此需要使用專門的技術來找到全域性最優解。

最佳化解

目的是確定可行區域中最大化或最小化目標函式的位置。這是透過使用單純形法和內點法等技術來實現的。

非線性最佳化的應用

非線性最佳化的關鍵應用或用例如下：

價格最佳化 - NLO 幫助具有非線性需求曲線的組織確定最有效的價格策略以最大化收入。商品的需求並不總是隨著價格線性下降，因此需要非線性模型來準確反映這種趨勢。
供應鏈最佳化 - 物流中可能存在非線性成本結構（例如，規模經濟或運輸路線）。NLO 幫助確定最佳資源分配，同時考慮非線性成本函式。
投資組合最佳化 − 在金融領域，非線性最佳化 (NLO) 用於管理具有非線性關係的投資組合中的風險和收益。一個典型的例子是基於資產收益方差（二次函式）來最佳化投資組合。
醫療保健 − NLO 可用於根據各種治療方法、患者預後和成本之間的非線性關係來最佳化治療方案。例如，醫院可以使用它來降低運營成本，同時考慮與治療預後相關的非線性風險。
機器學習模型訓練 − 非線性最佳化廣泛用於機器學習中訓練模型，例如神經網路，其中成本函式通常是非線性的。

3. 整數規劃 (IP) 或整數最佳化 (IO)

整數最佳化 (IO)，有時也稱為整數規劃 (IP)，是一種最佳化型別，其中決策變數儲存整數值。整數規劃是一種用於規範性分析的最佳化技術，用於使用整數變數（通常稱為整數）來識別問題的最優解。其目標是在降低成本和資源的同時增加利潤。這使得它在決策基於“是/否”決策或數字不能是分數（例如，物品、人員和機器）的情況下特別有效。在規範性分析中，整數最佳化有助於在這種限制下做出最佳或接近最佳的決策。

整數最佳化是如何工作的？

整數最佳化的工作原理基於以下概念：

目標函式 − 此函式的主要目標是最大化或最小化特定函式（例如，利潤、成本、時間），但使用整數決策變數。例如 - 最大化 Z = c₁x₁+c₂x₂+...+c_nx_n 其中 Z 是要最大化的目標，x₁,x₂,...,x_n 是整數決策變數，c₁,c₂,...,c_n 是係數。
約束條件 − 約束條件是線性不等式或等式，但某些或所有決策變數必須是整數。例如：a₁x₁+a₂x₂+...+a_nx_n≤b 其中 x₁,x₂,...,x_n 是整數決策變數。

整數最佳化的應用

關於規範性分析，整數最佳化的一些關鍵應用如下：

供應鏈管理 − 最佳化生產、運輸和分銷，同時考慮卡車、工廠或倉庫數量等特定變數。
員工排班 − 最佳化員工分配或輪班安排，同時遵守法律要求、員工可用性和需求。
資本預算 − 將固定預算分配給多個專案，每個專案需要特定的投資金額（例如，固定成本）。
投資組合最佳化 − 選擇一個投資組合，在滿足某些投資金額必須離散的要求下，最佳化收益並最小化風險。
網路設計和最佳化 − 最佳化通訊、運輸或公用事業網路的架構，同時保持設施、連線或資源的數量離散。
生產和製造計劃 − 使用整數限制最佳化生產計劃、機器利用率或資源分配。
設施選址規劃 − 最佳化設施（例如倉庫、工廠、零售店）的數量和位置，其中決策需要離散的選擇。
運輸和物流最佳化 − 做出具體的決策以降低運輸成本或時間（例如，車輛、路線或交付的數量）。
醫療資源分配 − 最佳化醫生、護士和醫療裝置等資源的分配，其中決策必須以大量數字做出。

列印頁面