資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究在半圓內接正方形內接最大的萊洛三角形在C語言中？
萊洛三角形是由三個圓的交集形成的形狀，每個圓的圓心都在另外兩個圓的邊界上。它的邊界是等寬曲線，除了圓本身之外，最簡單和最著名的等寬曲線。等寬意味著每兩條平行支撐線的間距相同，與它們的方向無關。因為它的所有直徑都相同。
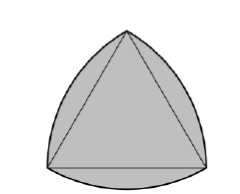
萊洛三角形的邊界是基於等邊三角形的等寬曲線。每條邊的所有點都與對面的頂點等距。
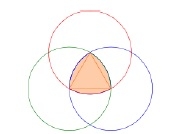
如何構造萊洛三角形
萊洛三角形的公式：
如果萊洛三角形的曲線基於等邊三角形，且三角形的邊長為h，則萊洛三角形的面積為：
A = (π * h2) / 2 – 2 * (等邊三角形的面積) = (π – √3) * h2 / 2 = 0.70477 * h2
半圓內接正方形內接最大的萊洛三角形
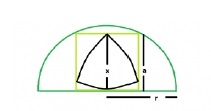
如果半圓內接正方形內接最大的萊洛三角形，則它看起來像上圖所示。
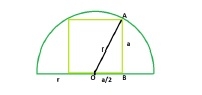
如果半圓內接最大的正方形，則它看起來像上圖所示
設r為半圓的半徑，a為正方形的邊長。
直角三角形AOB −
a2 + (a/2)2 = r2
5*(a2/4) = r2
a2 = 4*(r2/5) 即正方形的面積
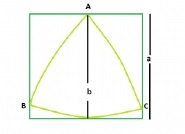
正方形內接最大的萊洛三角形
萊洛三角形的面積為0.70477 * b2，其中b是支撐萊洛三角形的平行線之間的距離。
支撐萊洛三角形的平行線之間的距離 = 正方形的邊長，即a
萊洛三角形的面積，A = 0.70477 * a2
Input:x = 5 Output: 14.0954
解釋
這裡給出一個半徑為r的半圓，它內接一個正方形，而正方形又內接一個萊洛三角形。求該萊洛三角形的最大可能面積。
內接於半圓的正方形的邊長為：a = 2r/√5
x = a。
x = 2*r/√5
萊洛三角形的面積 −
A = 0.70477*x^2 = 0.70477*(r^2/5)
示例
#include <stdio.h>
#include <math.h>
int main() {
float r = 5;
float x = (2 * r) / sqrt(5);
float A = 0.70477 * pow(x, 2);
printf("The area is %f",A);
return 0;
}輸出
The area is 14.095401
更新於： 2019年10月4日
85 次瀏覽
廣告