等腰三角形的面積

---

引言

等腰三角形的面積是指等腰三角形三條邊所包圍的平面區域的大小。它表示在二維空間中等腰三角形所包圍的面積。計算等腰三角形面積的常用公式是三角形底乘以高的一半。本教程將詳細解釋等腰三角形的面積、公式及其推導，並附帶一些例題，幫助你更好地理解這個主題。等腰三角形是根據邊長分類的一種三角形，它有兩條邊或兩個角相等。在本教程中，我們將學習等腰三角形的面積。

等腰三角形

在幾何學中，等腰三角形是指有兩條邊長度相等的三角形。可以定義為恰有兩條邊長度相等，或至少有兩條邊長度相等，後一種定義包含正三角形作為特例。等腰三角形的例子包括等腰直角三角形、黃金三角形、雙錐體的面以及一些卡塔蘭立體。

等腰三角形的面積

等腰三角形佔據的整個二維空間被稱為它的面積。等腰三角形的面積可以透過多種方法計算，具體取決於已知的等腰三角形的元素。以下是使用高計算等腰三角形面積的基本公式：

$$\mathrm{面積=\frac{1}{2}×底×高}$$

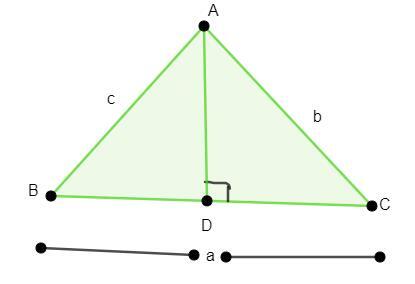
在上圖三角形ABC中，BC是底，AD是高。

在上圖三角形ABC中，BC是底，AD是高。

為了求出高，我們使用勾股定理如下：

$$\mathrm{DC^2+AD^2=AC^2}$$

$$\mathrm{\frac{a^2}{4}+AD^2=b^2}$$

$$\mathrm{AD^2=\frac{4b^2-a^2}{4}}$$

所以，

$$\mathrm{AD=\frac{1}{2} \sqrt{4b^2-a^2 }}$$

因此，三角形的面積由下式給出：

$$\mathrm{面積=\frac{1}{2}×底×高}$$

$$\mathrm{面積=\frac{1}{2}×a×\frac{1}{2} \sqrt{4b^2-a^2 }=\frac{1}{4} a\sqrt{4b^2-a^2 }}$$

例題

1)等腰三角形的周長為60釐米。如果其中一條等邊長為20釐米，則求不等邊的長度。

答案

設a,a & b為等腰三角形的三個邊長，則：

$$\mathrm{a+a+b=60}$$

$$\mathrm{2a+b=60}$$

$$\mathrm{2(20)+b=60}$$

$$\mathrm{b=60-40=20}$$

因此，不等邊的長度為20釐米。

2)一條等邊長為3釐米，底邊長為6釐米的等腰三角形的面積是多少？

答案

使用公式 $\mathrm{面積=\frac{1}{4} a\sqrt{4b^2-a^2}}$，我們得到：

$$\mathrm{面積=\frac{1}{4}×3×\sqrt{4(6)^2-3^2}=\frac{3×\sqrt{135}}{4}=\frac{9\sqrt{15}}{4} \:平方釐米}$$

3)等腰三角形的底邊為7，其中一條等邊為5。三角形的周長是多少？

答案

設a,a & b為等腰三角形的三個邊長，則：

$$\mathrm{a+a+b=P}$$

$$\mathrm{2a+b=P}$$

$$\mathrm{2(5)+7=P}$$

$$\mathrm{P=10+7=17}$$

因此，等腰三角形的周長為17釐米。

4)如果等腰三角形的底邊為18釐米，高為9釐米，則求其面積。

答案：等腰三角形的面積由下式給出：

$$\mathrm{面積=\frac{1}{2}×底×高}$$

$$\mathrm{面積=\frac{1}{2}×18×9=9×9=81\: 平方釐米}$$

5)求面積為100平方釐米，底邊為16釐米的等腰三角形的高。

答案：等腰三角形的面積由下式給出：

$$\mathrm{面積=\frac{1}{2}×底×高}$$

$$\mathrm{100=\frac{1}{2}×16×高}$$

$$\mathrm{高=\frac{100}{8}=\frac{25}{2}釐米}$$

因此，給定等腰三角形的高為12.5釐米

6)求面積為100平方釐米，高為16釐米的等腰三角形的底邊。

答案

等腰三角形的面積由下式給出：

$$\mathrm{面積=\frac{1}{2}×底×高}$$

$$\mathrm{100=\frac{1}{2}×底邊×16}$$

$$\mathrm{底邊=\frac{100}{8}=\frac{25}{2}釐米}$$

因此，等腰三角形的底邊為12.5釐米

7)一條等邊長為5釐米，底邊長為9釐米的等腰三角形的面積是多少？

答案：使用公式 $\mathrm{面積=\frac{1}{4} a\sqrt{4b^2-a^2}}$，我們得到

$$\mathrm{面積=\frac{1}{4}×5×\sqrt{4(9)^2-5^2}=\frac{5×\sqrt{315}}{4} \: 平方釐米}$$

8)等腰三角形的底邊為11，其中一條等邊為10。三角形的周長是多少？

答案：設a,a & b為等腰三角形的三個邊長，則：

$$\mathrm{a+a+b=P}$$

$$\mathrm{2a+b=P}$$

$$\mathrm{2(10)+11=P}$$

$$\mathrm{P=20+11=31}$$

因此，等腰三角形的周長為31釐米。

9)等腰三角形的底邊為20，其中一條等邊為17。三角形的周長是多少？

答案

設a,a & b為等腰三角形的三個邊長，則：

$$\mathrm{a+a+b=P}$$

$$\mathrm{2a+b=P}$$

$$\mathrm{2(17)+20=P}$$

$$\mathrm{P=34+20=54}$$

因此，等腰三角形的周長為54釐米。

結論

• 等腰三角形是具有兩條相等邊長的三角形。

• 等腰三角形的面積可以使用底乘以高的一半的常用公式計算。

• 如果給出等腰三角形的邊長，則我們使用以下公式：

  $$\mathrm{面積=\frac{1}{4} a\sqrt{4b^2-a^2}}$$

常見問題解答

1.是什麼使等腰三角形獨一無二？

等腰三角形有兩條相等的邊和兩個相等的角。名稱來源於希臘語iso（相同）和skelos（腿）。等邊三角形是所有邊都相等的三角形，而不等邊三角形是所有邊都不相等的三角形。

2.等腰三角形的三個特徵是什麼？

等腰三角形的特徵如下：有兩條邊相等。等腰三角形的底邊指的是三角形的第三條邊，它與其他兩條邊不相等。與相等邊相對的兩個角相等。

3.關於等腰三角形，哪些總是正確的？

當等腰三角形的兩條邊相等時，與這兩條邊相對的角也相等。

4.存在多少種不同的等腰三角形？

等腰三角形通常分為幾種型別，包括等腰銳角三角形、等腰直角三角形和等腰鈍角三角形。

5.所有等腰三角形看起來都一樣嗎？

由於幾個原因，所有等腰三角形彼此之間都是不同的。兩條相等邊可以有相同的長度，但底邊和底角以及兩條相等邊之間夾角的度數會發生變化。

6.等腰三角形的五個特徵是什麼？

等腰三角形的性質如下：

• 它有兩條長度相同的邊。

• 等邊相對角的度數相同。

• 從頂點A到底邊BC的高是底邊BC的垂直平分線。

• 頂角A的角平分線是從頂點A到底邊BC的高。

7.等腰三角形的邊可以相等嗎？

由於每個等邊三角形也是等腰三角形，因此任何兩條相等的邊都有相等的對應角。

8.什麼是銳角等腰三角形？

根據定義，銳角等腰三角形沒有角度大於90度，至少有兩條全等的邊和至少兩個對應的角。

9.等腰三角形結實嗎？

等邊三角形和等腰三角形是自然界中最堅固的三角形，因為它們都有相等的邊長。長度應該相等的是中間以90度角相遇的兩條邊。