座標幾何中三角形的面積

---

引言

座標幾何中三角形的面積用於利用座標查詢三角形的面積。在幾何學中，三角形是一個有三條邊和三個頂點的三邊形。三角形的面積是在二維平面內三角形所覆蓋的空間量。

在幾何學中，三角形是一個封閉的二維圖形，具有三條邊、三個角和三個頂點。三角形被認為是最少邊數的多邊形。三角形是我們世界中具有廣泛特性和應用的形狀之一。三角形是一個封閉的二維圖形。它們是一種多邊形，其中三個角的總和通常等於180°。

在本教程中，我們將討論座標幾何中的三角形。

三角形

在幾何學中，三角形是具有三條邊和三個頂點的多邊形。它是二維的，具有三條直邊。三角形的三個角之和等於180°。一個平面包含一個三角形。根據其邊和角，三角形分為六種形式。

三角形的性質

三角形的性質有助於理解三角形各個邊和角之間的關係。

• 角和性質

  根據角和性質，三角形的三個內角之和始終為180°。

• 三角形由它的三條邊、三個角和三個頂點定義。

• 三角形的兩條邊的長度之和大於其第三邊的長度。

• 三角形的面積等於其底和高乘積的一半。

• 三角形的周長是三角形三條邊的和。

• 全等性質

全等性質指出，如果兩個三角形的對應邊和角都相等，則這兩個三角形全等。

利用座標計算三角形的面積

座標幾何是利用座標點研究幾何學的方法。如果在座標平面上給出三角形的三個頂點，則可以確定三角形的面積。

考慮以下三個點：A(1,3)、B(4,1)和C(6,4)。當這三個點在平面上繪出時，它們是非共線的，這意味著它們可以作為三角形的頂點，如下所示：

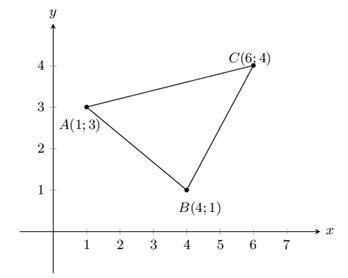
現在我們可以使用座標幾何來計算這個三角形的面積。讓我們在下面的部分中瞭解更多關於它的資訊。

在座標幾何中計算三角形面積的方法

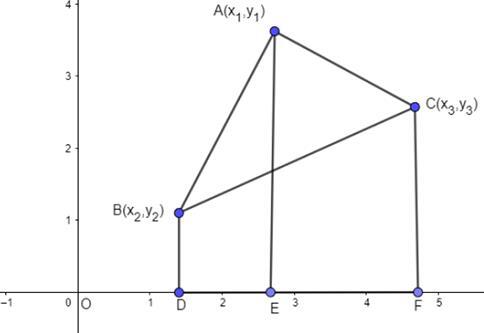
在座標幾何中，我們利用三個頂點的座標來計算三角形的面積。考慮三角形ABC，其頂點為A (x₁,y₁) B (x₂,y₂)和C (x₃,y₃)。

在此圖中，從三角形的頂點到水平軸繪製了垂線AE、CF和BD。形成了三個梯形：BAED、ACFE和BCFD。

三角形的面積可以用這三個梯形的面積來表示。

面積(ΔABC) = 面積(梯形BAED) + 面積(梯形ACFE) - 面積(梯形BCFD)

考慮任何一個梯形，例如BAED。它有兩個底，BD和AE，以及一個高DE。BD和AE分別是B和A的y座標，而DE是A和B的x座標之差。另外兩個梯形的底和高也很容易計算。因此，我們有

面積(ΔABC) = 面積(梯形BAED) + 面積(梯形ACFE) - 面積(梯形BCFD)

$$\mathrm{面積(\Delta ABC) =\frac{1}{2}×[(y_2+y_1)×(x_1-x_2)]+\frac{1}{2}×[(y_1+y_3)×(x_3-x_1)]+\frac{1}{2}×[(y_2+y_3)×(x_3-x_2)]}$$

$$\mathrm{面積(面積(\Delta ABC) =\frac{1}{2}×|x_1 (y_2-y_3)+x_2 (y_3-y_1)+x_3 (y_1-y_2)|}$$

此公式也可以寫成行列式形式：

$$\mathrm{面積 = \begin{bmatrix} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{bmatrix}}$$

三角形的面積不能為負。如果我們得到一個負結果，我們應該計算面積的數值，而不考慮負號。

利用三角形的面積判斷三點共線

• 共線點是指位於同一條直線或同一平面上的點。在歐幾里得幾何中，位於一條線上彼此靠近或遠離的兩點或多點被稱為共線。

• 如果由這三個點形成的三角形的面積等於零，則這三個點是共線的。

• 在三角形面積公式中，代入給定的三個點的座標。如果三角形的面積為0，則稱給定的點是共線的。

例題

1) 求座標為A (0,0) B (0,1)和C (1,0)的三角形的面積。

答案：已知座標為A (0,0) B (0,1)和C (1,0)。

我們知道行列式形式的公式為：

$$\mathrm{面積 = \begin{bmatrix} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{bmatrix}}$$

現在代入值：

$$\mathrm{面積 = \begin{bmatrix}0 & 0 & 1 \\0 & 1 & 1 \\1 & 0 & 1\end{bmatrix}}$$

現在沿第一行展開 $\mathrm{面積(\Delta ABC) =\frac{1}{2}× |0+0+1(0-1)|}$

$$\mathrm{\Rightarrow \frac{1}{2}}$$

2) 求給定三角形的面積。

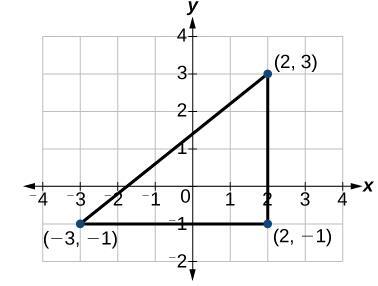
答案：已知座標為A (-3,-1) B (2,-1)和C (2,3)。

我們知道行列式形式的公式為：

$$\mathrm{面積 = \begin{bmatrix} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{bmatrix}}$$

現在代入值：

$$\mathrm{面積 = \begin{bmatrix}-3 & -1 & 1 \\2 & -1 & 1 \\2 & 3 & 1\end{bmatrix}}$$

現在沿第一行展開面積(ΔABC)

$$\mathrm{\Rightarrow \frac{1}{2} |[-3(-1-3)+1(2-2)+1(6+2)]|}$$

$$\mathrm{\Rightarrow 8}$$

3) 求給定三角形的面積。

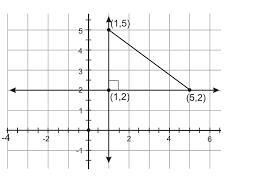
答案：已知座標為A (1,2) B (5,2)和C (1,5)。

我們知道行列式形式的公式為：

$$\mathrm{面積 = \begin{bmatrix} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{bmatrix}}$$

現在代入值：

$$\mathrm{面積 = \begin{bmatrix}1 & 2 & 1 \\5 & 2 & 1 \\1 & 5 & 1\end{bmatrix}}$$

現在沿第一行展開面積(ΔABC)

$$\mathrm{\Rightarrow \frac{1}{2} |[1(2-5)-2(5-1)+1(25-2)]|}$$

$$\mathrm{\Rightarrow 12}$$

結論

在幾何學中，三角形是一個有三條邊和三個頂點的三邊形。三角形的面積是它在二維平面中佔據的空間。如果由這三個點形成的三角形的面積等於零，則這三個點是共線的。

常見問題

1. 座標幾何是什麼意思？

座標幾何是數學的一個分支，它有助於在二維平面上呈現幾何圖形並學習這些圖形的特性。

2. 什麼是三角形？

在幾何學中，三角形是具有三條邊和三個頂點的多邊形。它是二維的，具有三條直邊。

3. 三角形的面積是多少？

三角形的面積是它在二維平面中佔據的空間。

4. 求三角形面積的公式是什麼？

求三角形面積的公式：

$$\mathrm{面積 = \begin{bmatrix} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{bmatrix}}$$

5. 如何判斷給定的三個點是否共線？

如果由這三個點形成的三角形的面積等於零，則這三個點是共線的。