資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究什麼是節點分析？
節點分析是一種確定電路中支路電流的方法。在這種方法中，一個節點被選為參考節點。電路中所有節點的電位都相對於此參考節點測量。
節點分析基於基爾霍夫電流定律，該定律指出“節點處所有進入電流和離開電流的代數和等於零”。
$$\mathrm{\sum\:\mathit{I}_{incoming}\:+\:\sum\:\mathit{I}_{outgoing}=0}$$
節點 – 節點是網路中兩個或多個電路元件連線的點。
結點 – 結點是三個或多個電路元件連線的點。
在節點分析中，我們必須找到結點處的電位而不是節點處的電位。所需的獨立節點對方程數比網路中結點數少一個。也就是說，如果“n”是獨立節點方程數，“j”是結點數，則：
$$\mathrm{n\:=\:\mathit{j}\:-\:1}$$
解釋
考慮以下所示的電路。在電路中，A、B、C 和 D 是四個節點，節點 B 和 D 是結點，其中節點 D 被選為參考節點。因此，
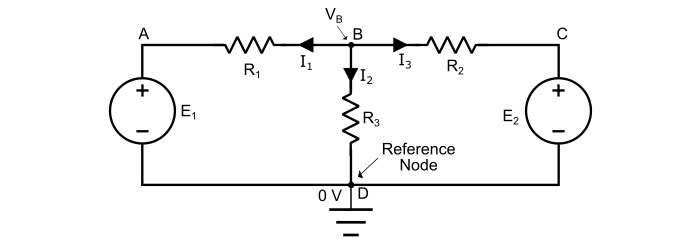
假設節點 B 處的電壓 VB 高於電路中所有其他節點。
在節點 B 處應用 KCL，我們得到：
$$\mathrm{\mathit{I}_{1}\:+\:\mathit{I}_{2}\:+\:\mathit{I}_{3}=0}\:\:\:…(1)$$
現在，根據歐姆定律，支路電流為：
$$\mathrm{\mathit{I}_{1}=\frac{\mathit{V}_{B}\:-\mathit{E}_{1}\:-0}{\mathit{R}_{1}}=\frac{\mathit{V}_{B}\:-\:E_{1}}{\mathit{R}_{1}}}$$
$$\mathrm{\mathit{I}_{2}=\frac{\mathit{V}_{B}\:-\mathit{E}_{2}\:-0}{\mathit{R}_{2}}=\frac{\mathit{V}_{B}\:-\:E_{2}}{\mathit{R}_{2}}}$$
並且，
$$\mathrm{\mathit{I}_{3}=\frac{\mathit{V}_{B}\:-0}{\mathit{R}_{3}}=\frac{\mathit{V}_{B}}{\mathit{R}_{3}}}$$
將 I1、I2 和 I3 的值代入方程 (1)，我們得到：
$$\mathrm{\frac{\mathit{V}_{B}\:-\mathit{E}_{1}}{\mathit{R}_{1}}+\frac{\mathit{V}_{B}\:-E_{2}}{\mathit{R}_{2}}+\frac{\mathit{V}_{B}}{\mathit{R}_{3}}=0}\:\:\:…(2)$$
可以透過求解方程 (2) 獲得節點 B 處的電壓 VB。由於電動勢 E1、E2 和電阻值是已知的。因此，我們可以確定支路電流的值。
數值示例
使用節點分析法求解下圖所示電路中各支路的電流。
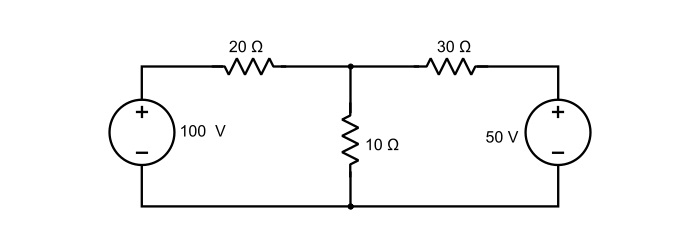
解答
在電路圖中標記各支路的電流。如果解出的任何電流值為負數，則表示電流的實際方向與假設方向相反。取點 B 作為參考節點。因此，
在節點 A 處應用 KCL，
$$\mathrm{\mathit{I}_{1}\:+\:\mathit{I}_{2}\:+\:\mathit{I}_{3}=0}\:\:\:…(3)$$
根據歐姆定律，
$$\mathrm{\mathit{I}_{1}=\frac{\mathit{V}_{A}-100}{20}}$$
$$\mathrm{\mathit{I}_{2}=\frac{\mathit{V}_{A}}{10}}$$
並且
$$\mathrm{\mathit{I}_{3}=\frac{\mathit{V}_{A}-50}{30}}$$
將 I1、I2 和 I3 的值代入方程 (3)，我們得到：
$$\mathrm{\frac{\mathit{V}_{A}-100}{20}+\frac{\mathit{V}_{A}}{10}+\frac{\mathit{V}_{A}-50}{30}=0}$$
$$\mathrm{\Rightarrow\frac{3(\mathit{V}_{A}-100)+6\mathit{V}_{A}+2(\mathit{V}_{A}-50)}{60}=0}$$
$$\mathrm{\Rightarrow\:3\mathit{V}_{A}-300+6\mathit{V}_{A}+2\mathit{V}_{A}-100=0}$$
$$\mathrm{\Rightarrow\:11\mathit{V}_{A}=400}$$
$$\mathrm{\mathit{V}_{A}=\frac{400}{11}=36.36\mathit{V}}$$
因此，節點 A 處的電壓等於 36.36 V，因此支路電流為：
$$\mathrm{電流\:\mathit{I}_{1}=\frac{\mathit{V}_{A}-100}{20}=\frac{36.36-100}{20}=-3.182\:A}$$
$$\mathrm{電流\:\mathit{I}_{2}=\frac{\mathit{V}_{A}}{20}=\frac{36.36}{20}=3.636\:A}$$
$$\mathrm{電流\:\mathit{I}_{3}=\frac{\mathit{V}_{A}-50}{30}=\frac{36.36-50}{30}=0.455\:A}$$
電流 I1 和 I3 的負號表示電流的實際方向與假設方向相反。
1K+ 瀏覽量
