資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝學
法學什麼是網孔電流分析法？
在這種方法中，將基爾霍夫電壓定律應用於網路，根據網孔電流編寫網孔方程。然後透過對該支路共有的網孔電流進行代數和來求出支路電流。
基爾霍夫電壓定律
基爾霍夫電壓定律（KVL）指出，在網孔中，所有電動勢和電壓降的代數和等於零，即：
$$\mathrm{\sum\:emfs\:+\:\sum\:Voltage\:Drops = 0}$$
網孔 - 網孔是最基本的迴路形式，它不能再細分為其他迴路，即網孔不包含任何內迴路。
解釋
每個網孔都分配一個單獨的網孔電流。為方便起見，假設所有網孔電流都沿一個方向流動（順時針或逆時針）。如果網孔電流的方向是任意的，也會得到相同的結果。
如果兩個網孔電流流過一個電路元件，則該元件中的實際電流是這兩個電流的代數和。
應用KVL根據網孔電流為每個網孔編寫方程。在編寫網孔方程時，電勢升高取正號，電勢降低取負號。
如果解的任何網孔電流值是負數，則意味著該網孔電流的真實方向與假設方向相反。
在下面的電路中應用KVL來編寫網孔方程，如下所示：
在ABDA網孔中應用KVL，
$$\mathrm{\mathit{E}_{1}-\mathit{I}_{1}\mathit{R}_{1}-(\mathit{I}_{1}-\mathit{I}_{2})\mathit{R}_{3}=0}$$
$$\mathrm{\Rightarrow\:\mathit{E}_{1}=\mathit{I}_{1}\mathit{R}_{1}-(\mathit{I}_{1}-\mathit{I}_{2})\mathit{R}_{3}}$$
$$\mathrm{\Rightarrow\:\mathit{E}_{1}=\mathit{I}_{1}(\mathit{R}_{1}\:+\:\mathit{R}_{3})-\mathit{I}_{2}\mathit{R}_{3}}\:\:\:… (1)$$
在BCDB網孔中應用KVL，
$$\mathrm{-\mathit{I}_{2}\mathit{R}_{2}-\mathit{E}_{2}(\mathit{I}_{2}-\mathit{I}_{1})\mathit{R}_{3}=0}$$
$$\mathrm{\Rightarrow\:\mathit{E}_{2}=\mathit{I}_{1}\mathit{R}_{3}-\mathit{I}_{2}(\mathit{R}_{2}\:+\:\mathit{R}_{3})}\:\:\:… (2)$$
透過同時求解方程（1）和（2），可以得到網孔電流I1和I2。一旦得到網孔電流，就可以很容易地求出電路各支路的電流。
注意 – 網孔電流是虛構的量，無法測量。而支路電流是實際電流，因為它們實際上流過支路，可以測量。
數值例子
計算下面電路中每個支路的電流。
解答
分別為ABDA和BCDB網孔分配網孔電流I1和I2，如下圖所示。
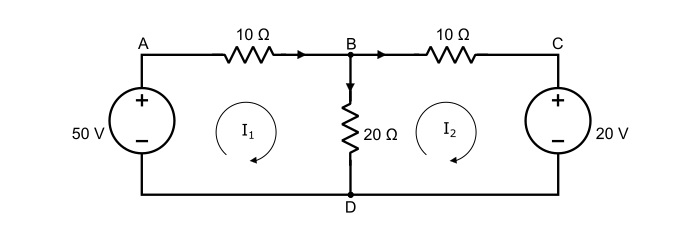
將KVL應用於ABDA網孔，
$$\mathrm{50-10\mathit{I}_{1}-20(\mathit{I}_{1}-\mathit{I}_{2})=0}$$
$$\mathrm{\Rightarrow\:50=30\mathit{I}_{1}-20\mathit{I}_{2}}$$
$$\mathrm{3\mathit{I}_{1}-2\mathit{I}_{2}=5\:\:\:… (3)}$$
將KVL應用於BCDB網孔，
$$\mathrm{-10\mathit{I}_{2}-20-20(\mathit{I}_{2}-\mathit{I}_{1})=0}$$
$$\mathrm{\Rightarrow\:-30\mathit{I}_{2}+20\mathit{I}_{1}=20}$$
$$\mathrm{2\mathit{I}_{1}-3\mathit{I}_{2}=2\:\:\:… (4)}$$
同時求解方程（3）和（4），網孔電流I1和I2為：
$$\mathrm{\mathit{I}_{1}=2.2\:A\:and\:\mathit{I}_{2}=0.8\:A}$$
因此，支路電流將為：
$$\mathrm{DAB支路的電流=\mathit{I}_{1}=2.2\:A\:\:\:(從A流向B)}$$
$$\mathrm{BCD支路的電流=\mathit{I}_{2}=0.8\:A\:\:\:(從B流向C)}$$
$$\mathrm{BD支路的電流=(\mathit{I}_{1}-I_{2})=2.2 − 0.8 = 1.4\:A\:\:\:(從B流向D)}$$
瀏覽量：531
