超大規模積體電路設計 - MOS電晶體

---

---

互補金氧半導體（CMOS）技術現已被廣泛用於在眾多不同應用中形成電路。如今的計算機、CPU和手機都利用CMOS，因為它具有若干關鍵優勢。CMOS具有低功耗、相對較高的速度、兩種狀態下均具有較高的噪聲容限，並且可以在較寬的電源和輸入電壓範圍內工作（前提是電源電壓固定）。

對於我們將討論的過程，可用的電晶體型別是金氧半導體場效應電晶體（MOSFET）。這些電晶體像“三明治”一樣形成，由半導體層（通常是切片或晶圓，來自單晶矽）、一層二氧化矽（氧化物）和一層金屬組成。

MOSFET的結構

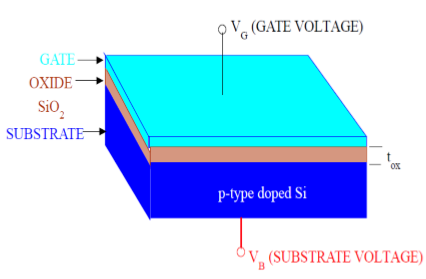
如圖所示，MOS結構包含三層：

• 金屬柵極電極

• 絕緣氧化物層（SiO₂）

• P型半導體（襯底）

MOS結構形成一個電容器，其中柵極和襯底作為兩個極板，氧化物層作為介電材料。介電材料（SiO₂）的厚度通常在10 nm到50 nm之間。可以透過施加到柵極和襯底端子的外部電壓來控制襯底內的載流子濃度和分佈。現在，為了理解MOS結構，首先考慮P型半導體襯底的基本電學特性。

半導體材料中載流子的濃度始終遵循質量作用定律。質量作用定律表示為：

$$n.p=n_{i}^{2}$$

其中，

• n是電子載流子濃度

• p是空穴載流子濃度

• n_i是矽的本徵載流子濃度

現在假設襯底均勻摻雜了受主（硼）濃度N_A。因此，p型襯底中的電子和空穴濃度為

$$n_{po}=\frac{n_{i}^{2}}{N_{A}}$$

$$p_{po}=N_{A}$$

這裡，摻雜濃度N_A比本徵濃度ni大（10¹⁵到10¹⁶ cm⁻³）。現在，為了理解MOS結構，請考慮p型矽襯底的能級圖。

如圖所示，導帶和價帶之間的帶隙為1.1eV。這裡，費米勢Φ_F是本徵費米能級（E_i）和費米能級（E_FP）之間的差值。

其中費米能級E_F取決於摻雜濃度。費米勢Φ_F是本徵費米能級（E_i）和費米能級（E_FP）之間的差值。

數學上表示為：

$$\Phi_{Fp}=\frac{E_{F}-E_{i}}{q}$$

導帶和自由空間之間的電勢差稱為電子親和勢，用qx表示。

因此，電子從費米能級移動到自由空間所需的能量稱為功函式（qΦ_S），其表示為

$$q\Phi _{s}=(E_{c}-E_{F})+qx$$

下圖顯示了構成MOS的元件的能帶圖。

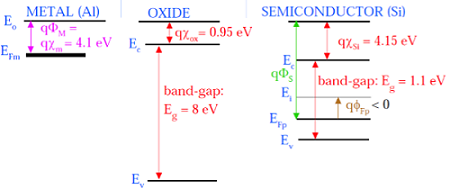
如上圖所示，絕緣SiO₂層具有8eV的大能帶隙，功函式為0.95 eV。金屬柵極的功函式為4.1eV。這裡，功函式不同，因此會在MOS系統上產生電壓降。下圖顯示了MOS系統的組合能帶圖。

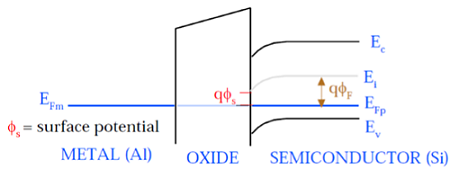
如圖所示，金屬柵極和半導體（Si）的費米勢能級處於相同電勢。表面處的費米勢稱為表面勢Φ_S，其大小小於費米勢Φ_F。

MOSFET的工作原理

MOSFET由一個MOS電容器組成，該電容器有兩個p-n結放置在靠近溝道區域，並且該區域受柵極電壓控制。為了使兩個p-n結反向偏置，襯底電勢保持低於其他三個端子的電勢。

如果柵極電壓超過閾值電壓（V_GS>V_TO），則會在表面上建立反型層，並且將在源極和漏極之間形成n型溝道。此n型溝道將根據V_DS值承載漏極電流。

對於V_DS的不同值，MOSFET可以在不同區域工作，如下所述。

線性區域

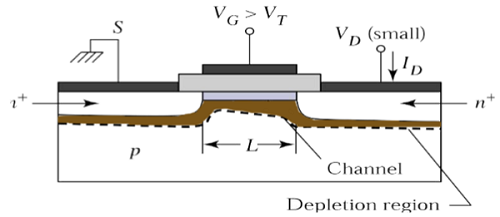
在V_DS = 0時，反型溝道區域存在熱平衡，漏極電流I_D = 0。現在，如果施加小的漏極電壓V_DS > 0，則與V_DS成正比的漏極電流將開始從源極流向漏極穿過溝道。

溝道為電流從源極流向漏極提供了連續路徑。這種工作模式稱為線性區域。下圖顯示了線上性區域工作時n溝道MOSFET的橫截面檢視。

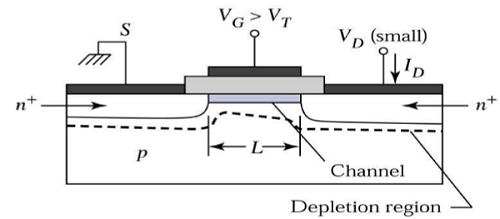
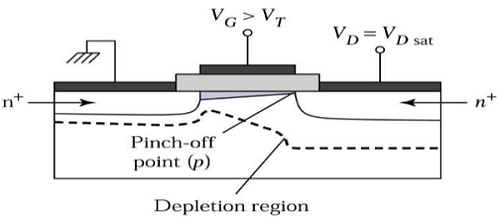
飽和區域邊緣

現在，如果增加V_DS，則溝道中的電荷和溝道深度在漏極端部減小。對於V_DS = V_DSAT，溝道中的電荷減小到零，這稱為夾斷點。下圖顯示了在飽和區域邊緣工作的n溝道MOSFET的橫截面檢視。

飽和區域

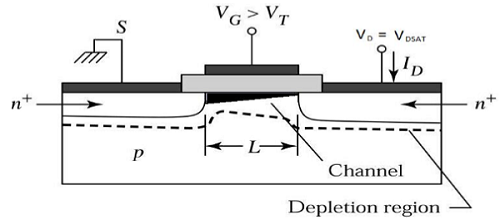
對於V_DS>V_DSAT，在漏極附近會形成耗盡表面，並且透過增加漏極電壓，該耗盡區域擴充套件到源極。

這種工作模式稱為飽和區域。來自源極進入溝道末端的電子進入漏極耗盡區域，並在高電場中加速向漏極移動。

MOSFET電流-電壓特性

為了理解MOSFET的電流-電壓特性，對溝道進行了近似。如果沒有此近似值，MOS系統的三維分析將變得複雜。用於電流-電壓特性的漸變溝道近似（GCA）將簡化分析問題。

漸變溝道近似（GCA）

考慮線上性模式下工作的n溝道MOSFET的橫截面檢視。這裡，源極和襯底連線到地。V_S = V_B = 0。柵極到源極（V_GS）和漏極到源極電壓（V_DS）電壓是控制漏極電流I_D的外部引數。

V_GS電壓設定為大於閾值電壓V_TO的電壓，以在源極和漏極之間建立溝道。如圖所示，x方向垂直於表面，y方向平行於表面。

這裡，y = 0位於源極端部，如圖所示。相對於源極的溝道電壓用V_C(Y)表示。假設閾值電壓VTO在源極到漏極之間的溝道區域內是恆定的。溝道電壓V_C的邊界條件為：

$$V_{c}\left ( y = 0 \right ) = V_{s} = 0 \,and\,V_{c}\left ( y = L \right ) = V_{DS}$$

我們還可以假設

$$V_{GS}\geq V_{TO}$$ 並且

$$V_{GD} = V_{GS}-V_{DS}\geq V_{TO}$$

令Q1(y)為表面反型層中的總移動電子電荷。此電子電荷可以表示為：

$$Q1(y)=-C_{ox}.[V_{GS}-V_{C(Y)}-V_{TO}]$$

下圖顯示了表面反型層的空間幾何形狀並指示其尺寸。當我們從漏極移動到源極時，反型層逐漸消失。現在，如果我們考慮溝道長度L的小區域dy，則此區域提供的增量電阻dR可以表示為：

$$dR=-\frac{dy}{w.\mu _{n}.Q1(y)}$$

這裡，負號是由於反型層電荷Q1的負極性，μ_n是表面遷移率，是常數。現在，將Q1(y)的值代入dR方程：

$$dR=-\frac{dy}{w.\mu _{n}.\left \{ -C_{ox}\left [ V_{GS}-V_{C\left ( Y \right )} \right ]-V_{TO} \right \}}$$

$$dR=\frac{dy}{w.\mu _{n}.C_{ox}\left [ V_{GS}-V_{C\left ( Y \right )} \right ]-V_{TO}}$$

現在，小區域dy中的電壓降可以表示為

$$dV_{c}=I_{D}.dR$$

將dR的值代入上述方程

$$dV_{C}=I_{D}.\frac{dy}{w.\mu_{n}.C_{ox}\left [ V_{GS}-V_{C(Y)} \right ]-V_{TO}}$$

$$w.\mu _{n}.C_{ox}\left [ V_{GS}-V_{C(Y)}-V_{TO} \right ].dV_{C}=I_{D}.dy$$

為了獲得整個溝道區域上的漏極電流ID，上述方程可以在溝道沿y = 0到y = L積分，電壓V_C(y) = 0到V_C(y) = V_DS，

$$C_{ox}.w.\mu _{n}.\int_{V_{c}=0}^{V_{DS}} \left [ V_{GS}-V_{C\left ( Y \right )}-V_{TO} \right ].dV_{C} = \int_{Y=0}^{L}I_{D}.dy$$

$$\frac{C_{ox}.w.\mu _{n}}{2}\left ( 2\left [ V_{GS}-V_{TO} \right ] V_{DS}-V_{DS}^{2}\right ) = I_{D}\left [ L-0 \right ]$$

$$I_{D} = \frac{C_{ox}.\mu _{n}}{2}.\frac{w}{L}\left ( 2\left [ V_{GS}-V_{TO} \right ]V_{DS}-V_{DS}^{2} \right )$$

對於線性區域V_DS < V_GS − V_TO。對於飽和區域，V_DS的值大於（V_GS − V_TO）。因此，對於飽和區域V_DS = (V_GS − V_TO)。

$$I_{D} = C_{ox}.\mu _{n}.\frac{w}{2}\left ( \frac{\left [ 2V_{DS} \right ]V_{DS}-V_{DS}^{2}}{L} \right )$$

$$I_{D} = C_{ox}.\mu _{n}.\frac{w}{2}\left ( \frac{2V_{DS}^{2}-V_{DS}^{2}}{L} \right )$$

$$I_{D} = C_{ox}.\mu _{n}.\frac{w}{2}\left ( \frac{V_{DS}^{2}}{L} \right )$$

$$I_{D} = C_{ox}.\mu _{n}.\frac{w}{2}\left ( \frac{\left [ V_{GS}-V_{TO} \right ]^{2}}{L} \right )$$