資料結構
網路
關係型資料庫管理系統(RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法學研究列車牽引力
什麼是牽引力？
推動機車車輪使列車前進所需的有效力稱為**牽引力**。它用𝐹𝑡表示，單位為牛頓。它是一個向量，始終作用於機車車輪的切線方向。
列車牽引力
推動列車在軌道上行駛所需的總牽引力等於以下各項之和：
用於直線和角加速度的牽引力 (𝐹𝑎)。
克服重力影響的牽引力 (𝐹𝑔)。
克服列車阻力的牽引力 (𝐹𝑟)。
因此，總牽引力表示為：
$$\mathrm{\mathit{F_{t}\mathrm{\: =\: }F_{a}\pm F_{g}\pm F_{r}}\; \cdot \cdot \cdot \left ( 1 \right )}$$
直線和角加速度的牽引力
根據動力學定律，使物體加速運動所需的力由下式給出：
$$\mathrm{力,\mathit{F}\mathrm{\: =\: }質量(\mathit{m})\times 加速度(\alpha )}$$
現在，考慮一輛重W噸的列車以α kmphps的加速度加速，則：
$$\mathrm{列車質量\mathrm{\: =\: }1000\mathit{W}\: kg}$$
$$\mathrm{加速度,\alpha \mathrm{\: =\: }\alpha \:kmphps\mathrm{\: =\: }\alpha \times \frac{1000}{3600}m/s^{2}\mathrm{\: =\: }0.2778\alpha \: m/s^{2} }$$
因此，直線加速度所需的牽引力為：
$$\mathrm{\mathit{F_{a}\mathrm{\: =\: }m\alpha \mathrm{\: =\: }\mathrm{1000}W\times \mathrm{0.2778\alpha } \mathrm{\: =\: }\mathrm{277.8}W\alpha}\: 牛頓$$
隨著列車的直線加速，列車的旋轉部件（如車輪和電機軸）也會在角方向加速。因此，所需的牽引力等於直線加速度所需的牽引力和旋轉部件角加速度所需的牽引力的算術和。
實際上，角加速度所需的牽引力取決於需要角加速度的旋轉部件的各個重量、回轉半徑等。因此，列車的等效加速重量取為𝑊𝑒，其比W高8%到15%。
因此，直線和角加速度所需的牽引力由下式給出：
$$\mathrm{\mathit{F_{a}\mathrm{\: =\: }}277.8\, \mathit{W_{e}\alpha}\: 牛頓\; \; \cdot \cdot \cdot \left ( 2 \right )}$$
克服重力影響的牽引力
當列車處於坡度（或斜坡）上時，等於沿斜坡的死重分量的重力作用於列車，並趨於使其向下運動。因此，由於坡度產生的力由下式給出：
$$\mathrm{\mathit{F_{g}\mathrm{\: =\: }mg}\: sin\, \theta \mathrm{\: =\: } 1000 \mathit{W_{g}}\: sin\theta}$$
但是，在鐵路工程中，坡度表示為在100米軌道距離內的高度上升（米），並表示為百分比坡度（G%）。現在從圖中，我們有：
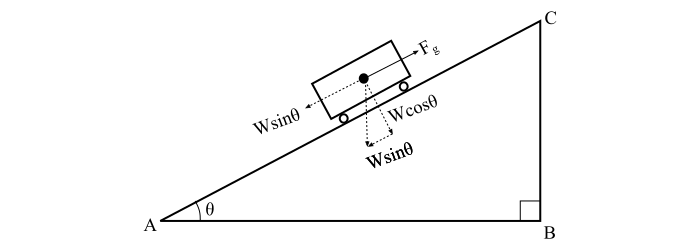
$$\mathrm{坡度或坡度,G \mathrm{\: =\: } sin\, \theta \mathrm{\: =\: }\frac{高度 \, (BC)}{沿軌道距離\: (AC)}}$$
$$\mathrm{\%G \mathrm{\: =\: } sin\, \theta \times 100}$$
$$\mathrm{\Rightarrow sin\, \theta \mathrm{\: =\: }\frac{\mathit{G}}{100}}$$
因此，
$$\mathrm{\mathit{F_{g}\mathrm{\: =\: }\mathrm{1000}Wg\times \frac{\mathit{G}}{\mathrm{100}}}\mathrm{\: =\: }10\mathit{WG}\times 9.81}$$
$$\mathrm{\Rightarrow \mathit{F_{g}\mathrm{\: =\: } \mathrm{9.81}\mathit{WG}}\; 牛頓\; \; \cdot \cdot \cdot \left ( 3 \right )}$$
其中，g = 9.81 m/s2，重力加速度。
克服列車阻力所需的牽引力
列車阻力包括當列車在直線平坦軌道上以均勻速度執行時抵抗列車運動的所有力。在這些條件下，驅動軸的全部能量輸出都用於克服列車阻力。
列車阻力主要是由於：
滾動裝置各個部件的摩擦。
軌道的摩擦。
空氣阻力。
這裡，前兩個組成部分構成了列車阻力的機械阻力分量。此外，列車阻力還取決於軌道形狀、尺寸和狀況等各種因素，並以**每噸死重的牛頓**表示。對於普通列車，比阻值從40到70 N/噸不等。
因此，列車阻力的通用表示式為：
$$\mathit{R\mathrm{\: =\: }k_{\mathrm{1}}\mathrm{\: +\: }k_{\mathrm{2}}V\mathrm{\: +\: }k_{\mathrm{3}}V^{\mathrm{2}}}$$
其中，𝑘1、𝑘2和𝑘3是常數，其值取決於列車和軌道。R是牛頓單位的阻力，V是kmph單位的速度。
因此，克服列車阻力所需的牽引力為
$$\mathit{F_{r}\mathrm{\: =\: }W\times r\; \; \cdot \cdot \cdot \mathrm{\left ( 4 \right )}}$$
其中，𝒓是列車死重每噸的比阻力。
因此，將方程式（2）、（3）和（4）中的值代入方程式（1），我們得到**執行列車所需的總牽引力**為：
$$\mathrm{\mathit{F_{t}\mathrm{\: =\: }F_{a}\pm F_{r}\mathrm{\: =\: }\mathrm{277.8}W_{e}\alpha \pm \mathrm{98.1}WG\mathrm{\: +\: }Wr}\: \: \cdot \cdot \cdot \left ( 5 \right )}$$
這裡，+號表示向上坡運動，-號表示向下坡運動。
8K+ 瀏覽量
