資料結構
網路
RDBMS
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究火車運動機理及牽引力的推導
火車運動機理
下圖顯示了電力機車的基本機理。
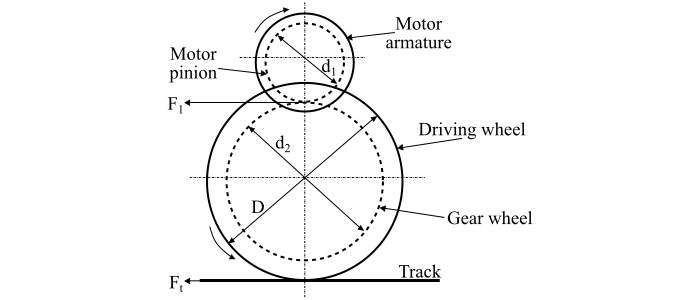
此處，驅動電機的電樞連線著一個直徑為 d1 的小齒輪。小齒輪邊緣的牽引力透過齒輪傳動到驅動輪。
令：
T = 電機輸出扭矩，單位為 Nm
F1 = 小齒輪上的牽引力
Ft = 車輪上的牽引力
$\gamma $ = 齒輪傳動比
d1 = 小齒輪直徑
d2 = 齒輪直徑
D = 驅動輪直徑
$\eta $ = 電機到驅動軸的動力傳遞效率
因此，電機輸出的扭矩由下式給出：
$$\mathrm{\mathit{T}\:=\:\mathit{F_{\mathrm{1}}}\:\times \:\frac{\mathit{d_{\mathrm{1}}}}{2}}$$
$$\mathrm{\therefore \mathrm{小齒輪上的牽引力,}\mathit{F_{\mathrm{1}}}\:=\:\frac{\mathrm{2}\mathit{T}}{\mathit{d_{\mathrm{1}}}}\:\:\:\cdot \cdot \cdot \mathrm{\left ( \mathrm{1} \right )}}$$
現在，傳遞到驅動輪的牽引力為：
$$\mathrm{\mathit{F_{\mathit{t}}}\:=\:\eta \mathit{F_{\mathrm{1}}}\mathrm{\left ( \frac{\mathit{d_{\mathrm{2}}}}{\mathit{D}} \right )}\:=\:\eta \cdot \frac{\mathrm{2}\mathit{T}}{\mathit{d_{\mathrm{1}}}}\mathrm{\left ( \frac{\mathit{d_{\mathrm{2}}}}{\mathit{D}} \right )}}$$
$$\mathrm{\Rightarrow \mathit{F_{\mathit{t}}}\:=\:\eta \mathit{T}\mathrm{\left ( \frac{\mathrm{2}}{\mathit{D}} \right )}\mathrm{\left ( \frac{\mathit{d_{\mathrm{2}}}}{\mathit{d_{\mathrm{1}}}} \right )}}$$
$$\mathrm{\because \mathrm{齒輪傳動比,}\gamma\:=\: \:\frac{\mathit{d_{\mathrm{2}}}}{\mathit{d_{\mathrm{1}}}}}$$
$$\mathrm{\mathit{F_{\mathit{t}}}\:=\:\mathrm{2}\eta \gamma \mathrm{\left ( \frac{\mathit{T}}{\mathit{D}} \right )}\:\:\:\cdot \cdot \cdot \mathrm{\left ( \mathrm{2} \right )}}$$
公式 (2) 給出了驅動輪上牽引力的值。
驅動輪與軌道之間的最大摩擦力等於 $\mu$W。其中，μ 是驅動輪與軌道之間的粘著係數，W 是作用在驅動軸上的火車重量，稱為粘著重量。粘著重量定義為作用在驅動輪上的總重量。
除非滿足以下條件，否則不會發生打滑
$$\mathrm{\mathit{F_{t}}> \mu \mathrm{W}}$$
因此，為了使火車不打滑地運動，牽引力應小於或最多等於 $\mu$W。
從以上討論可以清楚地看出，用於火車推進的牽引力的量值取決於作用在驅動輪上的重量以及驅動輪與軌道之間的粘著係數。
粘著係數
粘著係數定義為車輪不打滑時可施加的最大牽引力與粘著重量的比率，即：
$$\mathrm{\mu \:=\:\frac{\mathrm{車輪不打滑時可施加的最大牽引力}}{\mathrm{粘著重量}}}$$
此外，粘著係數會隨著速度的增加而降低。乾淨乾燥的鐵軌的粘著係數的正常值為 0.25，而潮溼或油膩的鐵軌的粘著係數低至 0.08。
由於在電力牽引中可以使用更高的牽引力值，因此可以使電力火車以更快的速度加速。這節省了時間，尤其是在停車距離較短的情況下。
數值示例
一列電力火車有 8 個電機與驅動輪相連，每個輪子的直徑為 80 釐米。確定每個電機產生的扭矩以加速火車。使火車在 30 秒內加速到 50 公里/小時的速度所需的牽引力為 117590 牛頓，齒輪傳動比為 4:1，齒輪傳動效率為 85%。
解答
已知資料：
車輪直徑，D = 80 釐米 = 0.8 米
牽引力，Ft = 117590 牛頓
齒輪傳動比，$\gamma$ = 4
齒輪傳動效率， $\eta$ = 85% = 0.85
因此，8 個電機產生的總扭矩為：
$$\mathrm{\mathit{T}\:=\:\frac{\mathit{F_{t}\times \mathit{D}}}{2\gamma \eta }\:=\:\frac{117590\times 0.8}{2\times 4\times 0.85}\:=\:13834.117\:\mathrm{NM}}$$
因此，每個電機產生的扭矩為：
$$\mathrm{\mathit{T_{\mathrm{each\:motor}}}\:=\:\frac{13834.117}{8}\:=\:1729.26\:\mathrm{NM}}$$
6K+ 次瀏覽
