證明語句 A = B * C + 20 的完整編譯過程,其中 A、B、C 為實數型別。
解決方案
符號表
| 序號 | 變數名 | 變數型別 |
|---|
| 200 | A | 浮點數 |
| 204 | B | 浮點數 |
| 208 | C | 浮點數 |
現在,我們將瞭解如何在每個級別執行編譯器階段以及它的工作原理。
這是第一步,它充當編譯器和原始碼之間的橋樑。它一次讀取原始碼一個字元,並將原始碼設計成一系列稱為標記的原子單元。
在這個階段,我們將瞭解如何對錶達式進行標記化。
A → 識別符號:(id, 1)
= → 運算子:賦值
B → 識別符號:(id, 2)
* → 運算子:乘法
C → 識別符號:(id, 3)
+ → 運算子:二元加法
20 → 常量:整數
最終表示式如下:
id1=id2*id3+20
它也稱為解析器。它接收來自上一階段(詞法分析)生成的標記作為輸入,並生成稱為語法樹或解析樹的分層結構。
在這個階段,它可以在對錶達式進行標記化後檢查語法。
表示式的語法分析如下:
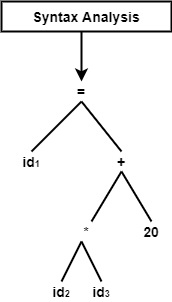
此階段以語法樹為輸入,並確定程式的語義準確性。然而,即使標記是準確的且語法正確的,它們也可能在語義上不精確。因此,語義分析器確定語句結構的語義 **(含義)**。在這個階段,它可以驗證語法樹的型別和語義操作。
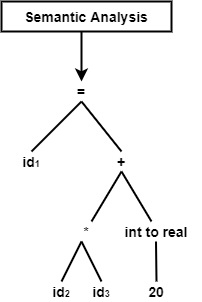
此階段以語法和語義上正確的形式作為輸入,並生成原始碼的相同中間表示法。在這個階段,我們將提供修改後的解析樹,並在轉換為中間程式後作為輸出,建立一個三地址碼。
T1=id2 * id3
T2=int to real (20)
T3=T1+T2
id1=T3
這是一個可選階段。它將源程式的中間表示轉換為高效的程式碼。在這個階段,它將以三地址碼作為輸入,並作為輸出,識別最佳化後的程式碼。
T1=id2 * id3
id1=T1+ 20.0
這是編譯過程的最後一步。它將最佳化的中間程式碼轉換為機器/彙編程式碼。它為程式中的變數分配記憶體位置。
在最後階段,可以看到如何將最終表示式修改為彙編程式。
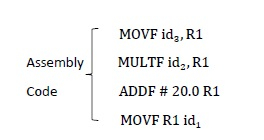
- 相關文章
- 如果\( A, B, C \)是\( \triangle A B C \)的內角,證明:\( \tan \frac{B+C}{2}=\cot \frac{A}{2} \)
- 如果\( A, B, C \)是\( \triangle A B C \)的內角,證明:\( \cos \frac{B+C}{2}=\sin \frac{A}{2} \)
- 如果 $2^{a}=3^{b}=6^{c}$,則證明 $ c=\frac{a b}{a+b} $
- 證明方程 $(x-a)(x-b)+(x-b)(x-c)+(x-c)(x-a)=0$ 的兩個根都是實數,但只有當 $a=b=c$ 時它們才相等。
- 證明:\( \left(x^{a-b}\right)^{a+b}\left(x^{b-c}\right)^{b+c}\left(x^{c-a}\right)^{c+a}=1 \)
- 驗證 $a ÷ (b+c) ≠ (a ÷ b) + (a ÷ c)$ 對於以下每個 $a,\ b$ 和 $c$ 的值是否成立。(a) $a=12,\ b=- 4,\ c=2$(b) $a=(-10),\ b = 1,\ c = 1$
- 證明以下文法是 LR(1)的\nS → A a |b A c |B c | b B a\nA → d\nB → d
- 如果 $a, b, c$ 是實數,且 $ac≠0$,則證明方程 $ax^2+bx+c=0$ 和 $-ax^2+bx+c=0$ 中至少有一個方程有實數根。
- 證明點 $P( a,\ b+c),\ Q( b,\ c+a)$ 和 $R( c,\ a+b)$ 共線。
- 如果方程 $a(b-c) x^2+b(c-a) x+c(a-b) =0$ 的根相等,則證明 $b(a+c) =2ac$。
- 如果 $A, B$ 和 $C$ 是三角形 $ABC$ 的內角,則證明: $sin\ (\frac{B+C}{2}) = cos\ \frac{A}{2}$
- 證明 $(a−b)^2,\ (a^2+b^2),\ (a+b)^2$ 成等差數列。
- C/C++ 中的編譯/連結過程是如何工作的?
- 證明點 $A( 4,\ 2),\ B( 7,\ 5),\ C( 9,\ 7)$ 共線。
- 設 $f(x)=3ax^2−4bx+c$ $(a,b,c∈R,a\neq 0)$,其中 $a,\ b,\ c$ 成等差數列。則方程 $f(x)=0$ 有多少個根?它們是實數嗎?






 資料結構
資料結構 網路
網路 關係資料庫管理系統 (RDBMS)
關係資料庫管理系統 (RDBMS) 作業系統
作業系統 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 語言程式設計
C 語言程式設計 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP