資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究證明以下文法是 LR(1) 的\nS → A a |b A c |B c | b B a\nA → d\nB → d
解決方案
步驟1 - 構造擴充文法
(0) S′ → S
(1) S → A a
(2) S → b A c
(3) S → B c
(4) S → b B a
(5) A → d
(6) B → d
步驟2 - 查詢閉包和 goto。構造 LR(1) 專案集。這裡所有框都表示新狀態。
LR(1) 分析表
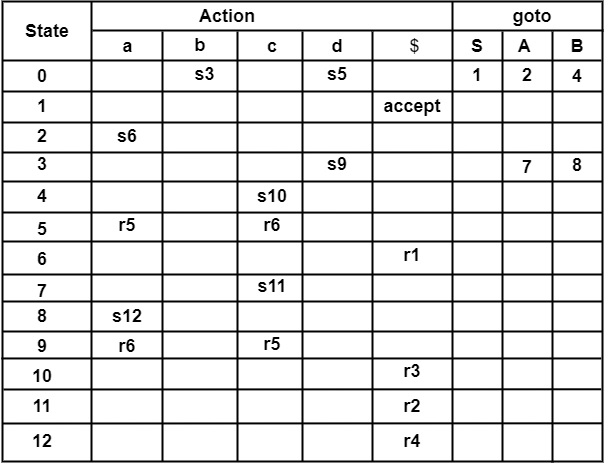
因此，LR(1) 分析表沒有多個條目。文法是 LR(1) 的。
LR(1) 或規範 LR 分析表的構造
輸入 - 擴充文法 G’。
輸出 - 規範 LR(1) 分析表
方法
填充“移進”條目 (s) - 應用 CLR 分析表構造的規則 (2a)。
考慮 I3 = goto(I0, c)
∴ Action[0, c] = shift 3
∴ 在第 0 行和第 c 列前面寫入 s3。
類似地，考慮另一個條目。
即，I7 = goto(I2, d)
∴ Action[2, d] = shift 7
∴ 在第 2 行和第 d 列前面寫入 s7。類似地，移進的其他條目填充到 Action 表中。
填充“歸約”條目 (r)
應用 CLR 分析表構造的規則 (2b)。考慮形如 A → α ∙ , a 的產生式
例如，考慮
I4 = goto(I0, d)
C → d ∙, c | d
這裡，C → d ∙, c | d 具有 A → α ∙ , a 的形式。因此，將 Action[4, c] 和 Action[4, d] 設定為 r3。
因為 C → d 是給定問題中第 3 個產生式。
∴ 在第 4 行和第 c 列和 d 列前面寫入 r3。
因為 c、d 在產生式 C → d ∙ , c | d 中是前瞻符號。
考慮另一個例子
I9 = goto(I9, C)
C → c C ∙, $
因為 C → c C 是給定問題中的產生式 (2)。
∴ 在第 9 行和第 $ 列前面寫入 r2，因為 $ 是附加到產生式的先行符號。
∴ Action[9, $] = r2
類似地，將所有歸約條目填充到分析表中。
goto 條目的填充
在 goto 中，只有非終結符以列的形式出現。
例如
I8 = goto(I3, C)
∴ Action[3, C] = 8
即，在第 3 行和第 C 列前面寫入 8。
“接受”條目的填充
應用 CLR 分析表的規則 (2c)
查詢包含形如 S′ → S ∙, $ 的產生式的狀態
∴ 它是狀態 I1
∴ 在第 1 行和第 $ 列前面寫入 accept。
6K+ 次瀏覽
