資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
Microsoft Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
JavaScript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
服裝設計
法學B → q
解答
步驟1 - 構造擴充文法
(0) S′ → S
(1) S → xAy
(2) S → xBy
(3) S → xAz
(4) A → qs
(5) A → q
(6) B → q
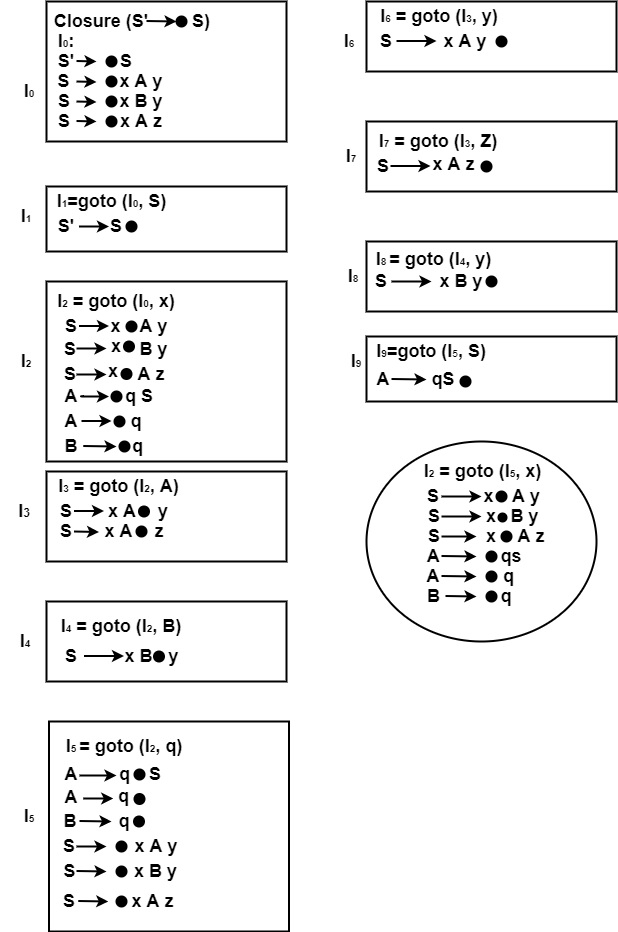
步驟2 - 查詢閉包和goto函式以構造LR(0)專案。此處方框代表新狀態，圓圈代表重複狀態。
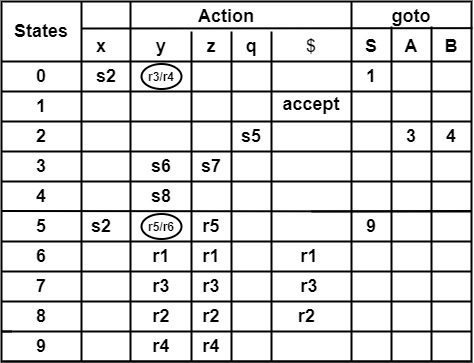
- 步驟3 - FOLLOW集的計算
S → xAy
FOLLOW(S) = {$} (1)
應用FOLLOW的規則(2a)。
將S → xAy與A → αBβ進行比較。
∴ FIRST(β) = FIRST(y) = {y}
∴ FOLLOW(A) = {y} (2)
規則(3)不可應用
- 因為S → xAy不能與A → αB比較
S → xBy
應用FOLLOW的規則(2a)。
將S → xBy與A → αBβ進行比較。
∴ FIRST(β) = {y}
∴ FOLLOW(B) = {y} (3)
- 步驟3 - FOLLOW集的計算
FOLLOW(S) = {$} (1)
規則(3)不可應用。
S → xAz
∴ FOLLOW(B) = {y} (3)
- ∴ FIRST(β) = {z}
∴ FOLLOW(A) = {z} (4)
A → qS
規則(2a)不可應用。因為A → qS不能與A → αBβ比較。
應用規則(3)
將A → qS與A → αB進行比較
∴ A = A, α = q, B = S
∴ FOLLOW(S) = {FOLLOW(A)} (5)
FOLLOW的規則(2a)和規則(3)不能應用於產生式A → q和B → q。
結合語句(1)到(5)
FOLLOW(A) = {y, z}
FOLLOW(S) = {$, y, z}
Ginni
