衛星通訊 - 軌道力學

---

---

我們知道，衛星繞地球執行的路徑稱為軌道。這條路徑可以用數學符號表示。軌道力學是研究存在於軌道上的衛星運動的學科。因此，通過了解軌道運動，我們可以輕鬆理解空間操作。

軌道要素

軌道要素是描述衛星軌道運動的引數。以下是軌道要素。

• 長半軸
• 偏心率
• 平近點角
• 近地點角距
• 傾角
• 升交點赤經

以上六個軌道要素定義了地球衛星的軌道。因此，可以根據軌道要素的值輕鬆區分一顆衛星與其他衛星。

長半軸

長半軸 (a)的長度決定了衛星軌道的尺寸。它是長軸的一半。它從中心穿過焦點到橢圓的邊緣。因此，它是軌道在軌道兩個最遠點處的半徑。

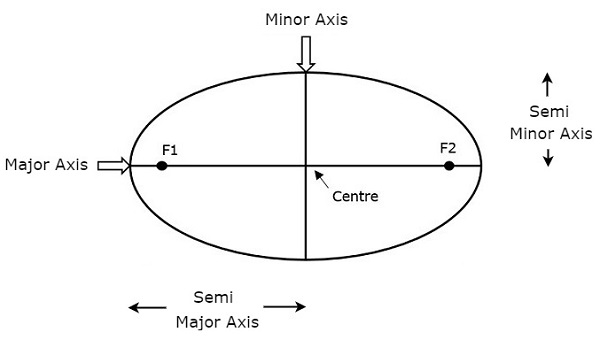
上圖顯示了長半軸和短半軸。長半軸 (a)的長度不僅決定了衛星軌道的尺寸，還決定了公轉週期。

如果將圓形軌道視為一個特例，則長半軸的長度將等於該圓形軌道的半徑。

偏心率

偏心率 (e)的值確定了衛星軌道的形狀。此引數表示軌道形狀與完美圓形的偏差。

如果橢圓軌道的長半軸和短半軸的長度分別為 a 和 b，則偏心率 (e)的數學表示式為

$$e = \frac{\sqrt{a^2 - b^2}}{a}$$

圓形軌道的偏心率值為零，因為 a 和 b 相等。而橢圓軌道的偏心率值介於零和一之間。

下圖顯示了不同偏心率 (e) 值的各種衛星軌道

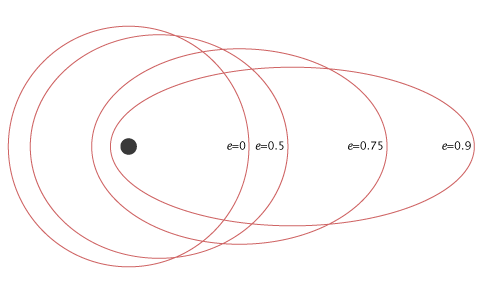
在上圖中，對應於偏心率 (e) 值為零的衛星軌道是圓形軌道。其餘三個衛星軌道為橢圓形，對應的偏心率 (e) 值分別為 0.5、0.75 和 0.9。

平近點角

對於一顆衛星，距離地球最近的點稱為近地點。平近點角 (M) 給出了衛星相對於近地點的角位置的平均值。

如果軌道是圓形的，則平近點角給出衛星在軌道中的角位置。但是，如果軌道是橢圓形的，則計算精確位置非常困難。此時，平近點角用作中間步驟。

近地點角距

衛星軌道在兩個點與赤道平面相交。第一個點稱為降交點，衛星在此處從北半球穿過南半球。第二個點稱為升交點，衛星在此處從南半球穿過北半球。

近地點角距 (ω)是升交點和近地點之間的角度。如果近地點和升交點都存在於同一點，則近地點角距將為零度

近地點角距在地球中心的軌道平面上沿衛星運動方向測量。

傾角

軌道平面和地球赤道平面之間的角度稱為傾角 (i)。它在升交點處測量，方向為東向北。因此，傾角以地球赤道為參考定義了軌道的方向。

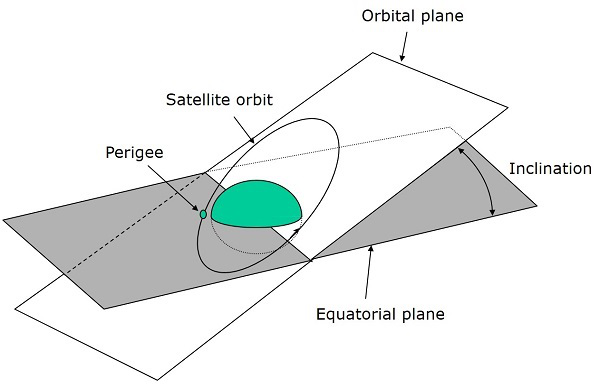
根據傾角，軌道有四種類型。

• 赤道軌道 - 傾角為零度或 180 度。

• 極軌道 - 傾角為 90 度。

• 順行軌道 - 傾角介於零和 90 度之間。

• 逆行軌道 - 傾角介於 90 和 180 度之間。

升交點赤經

我們知道升交點是衛星從南半球穿過北半球時穿過赤道平面的點。

升交點赤經(Ω)是白羊座線和升交點在赤道平面上的東向角度。白羊座也稱為春分點。

衛星的地面軌跡是地球表面上正好位於其軌道正下方的路徑。衛星的地面軌跡可以採用多種不同的形式，具體取決於軌道要素的值。

軌道方程

在本節中，讓我們討論與軌道運動相關的方程。

作用在衛星上的力

當衛星繞地球執行時，由於地球的萬有引力，它會受到來自地球的拉力。此力稱為向心力 (F₁)，因為此力使衛星傾向於向其靠近。

在數學上，由於地球作用在衛星上的向心力 (F₁) 可以寫成

$$F_{1} = \frac{GMm}{R^2} $$

其中，

• G 是萬有引力常數，等於 6.673 x 10^-11 N∙m²/kg²。

• M 是地球的質量，等於 5.98 x 10²⁴ Kg。

• m 是衛星的質量。

• R 是衛星到地球中心的距離。

當衛星繞地球執行時，由於太陽和月球的萬有引力，它會受到來自太陽和月球的拉力。此力稱為離心力 (F₂)，因為此力使衛星傾向於遠離地球。

在數學上，作用在衛星上的離心力 (F₂) 可以寫成

$$F_{2} = \frac{mv^2}{R} $$

其中，v 是衛星的軌道速度。

軌道速度

衛星的軌道速度是衛星繞地球執行的速度。當向心力和離心力平衡時，衛星不會偏離其軌道並以一定速度在該軌道上移動。

因此，使向心力 (F₁) 和離心力 (F₂) 相等。

$$\frac{GMm}{R^2} = \frac{mv^2}{R}$$

$$= > \frac{GM}{R} = v^2$$

$$= > v = \sqrt{\frac{GM}{R}}$$

因此，衛星的軌道速度為

$$v = \sqrt{\frac{GM}{R}}$$

其中，

• G 是萬有引力常數，等於 6.673 x 10^-11 N∙m²/kg²。

• M 是地球的質量，等於 5.98 x 10²⁴ Kg。

• R 是衛星到地球中心的距離。

因此，軌道速度主要取決於衛星到地球中心距離 (R)，因為 G 和 M 是常數。